Білет 1

1 . Матриці, основні поняття

Прямокутна таблиця чисел Аij,де і=1,2…m,та j=1,2… n,яка складається з m рядків та n стовпців називається матрицею. Якщо m=n ,то матриця називається квадратною.Кількість рядків квадратної матриці називається її порядком.Матриця,в якої лише один рядок називається матрицею-рядком,а матриця ,в якої лише один стовпець-матрицею-стовпцем.Матриця ,в якої всі елементи дорівнюють 0,називається нульовою.Уквадратних матрицях виділяють головну та побічну діагоналі .Квадратна матриця називається діагональною ,якщо всі її елементи ,крім елементів головної діагоналі,дорівнюють 0.Діагональна матриця називається скалярною,якщо всі елементи гголовної діагоналі рівні між собою. Матриця А називається узгодженою матриці В,якщо кількість стовпців матриці А дорівнює кількості рядків матриці В.

2 ) Різновиди рівняння площини у просторі:за трьома точками, у відрізках на осях, нормальне.

Рівняння площини , що проходить через три задані точки :

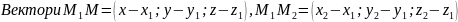
і 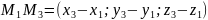лежать у шуканій площині, тобто компленарні, тому мішаний добуток цтх векторів дорівнює нулю (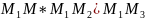 = 0.

Рівняння площини у відрізках на осях: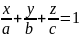 , де a,b,c – відрізки, які відсікає площина відповідно на осях Ox , Oy, Oz.

Нормальне рівняння площини: xc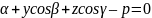os , де cos ,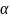

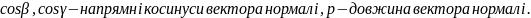
3) . Диференціювання параметрично заданих фу-й. Нехай фу-я f(x) диференційована в т. x. Тоді df=f ‘(x) ∙Δx назив. диференціалом фу-ї f(x) у т. х

Якщо х незалежний аргумент фу-ї, то за означ. вважають приріст Δx диференціалом аргумента х і познач. його dx, тобто dx= Δx. Тоді означ. диференціала фу-ї запис. За формулою: df(х)= f ‘(x) dx, dу=у' dx.

Похідна f ‘(x) є відношенням диференціала фу-ї до диференціала аргументу.

Похідна фу-я задана параметрично наз. фу-я, що задається рівнянням х=х(t), y=y(t). Якщо рівняння х=х(t) можна розв'язати відносно t: t= t(х), то, підставивши його у=у(t), одержимо у=у(t(х))=f(x). З формули маємо: f '(х)=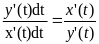 , якщо x’(t) ≠0.

5) Диференціальним рівнянням називається рівняння, яке містить незалежну змінну х , невідому функцію у(х) та її похідні або диференціали і має загальний вигляд F(x; y(x); (x), …yⁿ (x)) = 0.

Порядок диференціального рівняння визначається порядком старшої похідної, яка входить до даного диференціального рівняння.

Загальним розв ‘язком диф.рівняння назив. функція, яка містить стільки сталих, який порядок диференціального рівняння, і підстановка якої в дане диф.рівняння перетворює його в тотожність.

Одночасне задання диф.рівняння і відповідної кількості початкових умов назив. задачею Коші.

Білет 2

2)Рівняння площини, що проходить через задану точку перпендикулярно до заданого вектора. Загальне рівняння площини і його дослідження.

,

.

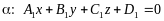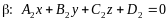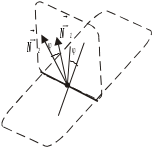
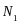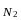Двогранний кут  між площинами  і  дорівнюватиме ку- ту між векторами і , перпендикулярними до цих площин (рис. 2.21), тому

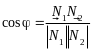. (2.28)

Якщо площини взаємно перпендикулярні, то 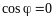і, розкривши скалярний добуток у формулі (2.28), дістанемо умову перпендикулярності двох площин:

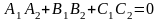. (2.29)

Якщо площини  і  паралельні між собою, то їхні вектори і — колінеарні, а отже, відповідні координати пропорційні, і ми маємо умову паралельності двох площин

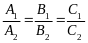. (2.30)

За аналогією з формулою знаходження відстані від точки до прямої на площині можна записати формулу знаходження відстані від точки 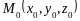до площини 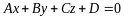. Вона набирає вигляду

.

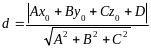3) Диференціювання неявно заданих фу-й. Якщо незалежна змінна х і функція у зв’язані рівнянням виду f(x, у) = 0, яке не розв’язане відносно у, то у називається неявною функцією х.

Незважаючи на те, що рівняння f(x, у) = 0 не розв’язане відносно у, можна знайти похідну від у по х. Прийом для знаходження по-хідної в цьому випадку полягає в тому що обидві частини рівняння f(x, у) = 0 диференціюємо по х з врахуванням, що у є функцією х, і із одержаного рівняння визначаємо у'.