8. Определение доверительной зоны регрессии
Найденные коэффициенты уравнения регрессии а, b, c и d зависят от параметров выборки и от выборки к выборке будут меняться. Поэтому уравнения регрессии носят приближенный характер. В связи с этим необходимо построить доверительную зону регрессии, в которой с доверительной вероятностью будет находиться истинная линия регрессии (для любой выборки из генеральной совокупности).
Найденные
теоретические значения фактора Y,
т.е.
,
также являются только оценками. Истинные
значения
с доверительной вероятностью
принадлежат интервалам
,
i = 1, 2, … ,
n
Размах доверительных интервалов определяется формулой:
.
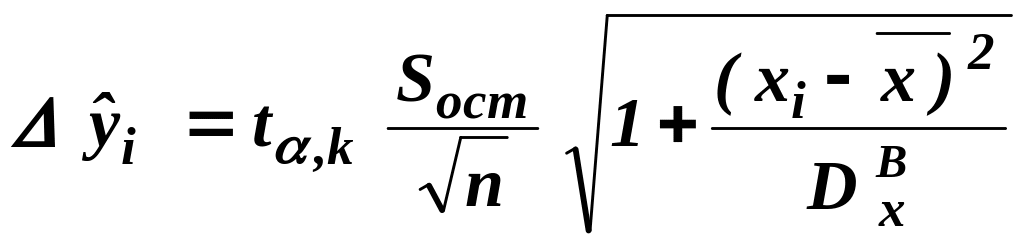
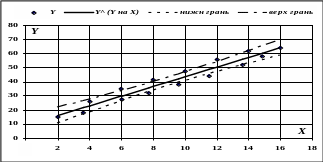
Если на графике построить доверительную зону регрессии (см. рис.), то с доверительной вероятностью можно утверждать, что истинная линия регрессии будет находиться в пределах этой зоны.
Доверительные интервалы для
вычисляются в столбце
BL
.
После выделения всего столбца, программируется формула
.
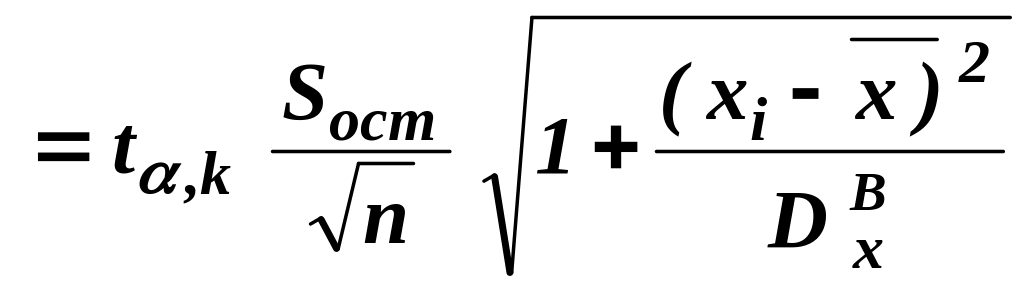
Внимание!
Для чисел
,
n,
и
указывается абсолютный
адрес или
имя ячейки; для величин
– имя столбца исходных данных для
фактора Х
(столбец N).
Закончить ввод сочетанием Ctrl + Enter.
В столбцах BM «нижн. грань» и BN «верхн. грань» вычисляются границы доверительной зоны:
.
Для построения доверительной зоны выделяются пять столбцов данных (вместе с заголовками): N, O, AG, BM и BN.
Далее следует вызвать Мастер Диаграмм и построить Точечную Диаграмму. (См. приведенную выше диаграмму).
Внимание! Следует отредактировать линии зоны регрессии таким образом, чтобы они были непрерывными (не включали маркеры, точки и другие метки). Саму линию регрессии и границы доверительной зоны для неё желательно указать разными цветами.
9. Прогноз и доверительный интервал для прогноза
Полученное уравнение регрессии применяется для вычисления прогнозного значения фактора Y. Задавая значение фактора Xp, по уравнению регрессии определяется Yp.
Так
как коэффициенты уравнения регрессии
носят приближенный характер, Yp
также
будет величиной приближенной. В связи
с этим необходимо построить доверительный
интервал (
),
которому с доверительной вероятностью
будет принадлежать истинное значение
прогнозируемой величины Yp.
Размах доверительного интервала
определяется по формуле:
.
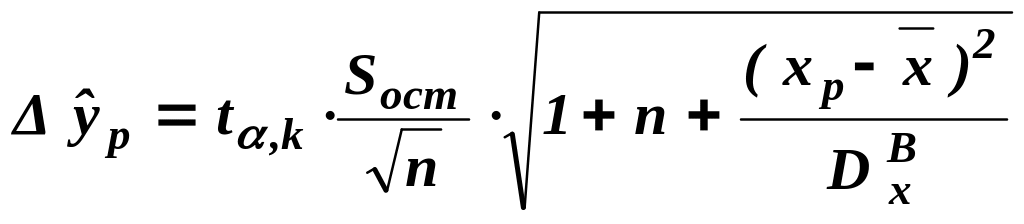
З
аданное
для прогноза значение Xp
скопировать из ячейки N23
в ячейку
BS29.В ячейке BV29 по формуле
вычислить
прогнозное значение фактора Yp.
Размах доверительного интервала определить в ячейке BS32.
В ячейках BU32 и BW32 указать границы доверительного
интервала для прогноза:
.
Вопросы для самоконтроля и контроля знаний
1. Дайте определение корреляционного поля. Каким образом по виду корреляционного поля формулируется гипотеза о характере связи между изучаемыми переменными?
2. Сформулируйте понятие уравнения регрессии. Какие типы уравнений регрессии наиболее часто используются в регрессионном анализе?
3. В чём заключается суть метода наименьших квадратов для определения математической модели парной линейной регрессии?
4. Что характеризует коэффициент корреляции в парной линейной регрессии? В каких пределах он изменяется?
5. Что характеризует коэффициент детерминации в парной линейной регрессии? Как он определяется?
6. Приведите пример анализа коэффициента детерминации в парной линейной регрессии. В каких пределах изменяется коэффициент детерминации и почему?
7. Дайте определение точечных оценок случайных величин.
8. В чем суть интервальных оценок случайных величин?
9. Опишите методику проверки статистической значимости коэффициентов корреляции и детерминации. Что такое доверительная вероятность?
10. Каким образом определяется критическое значение t – статистики Стьюдента и F – статистики Фишера? Как геометрически можно интерпретировать значения указанных статистик?
11. В чем суть интервальных оценок для коэффициентов уравнения парной линейной регрессии?
12. Сформулируйте понятие доверительной зоны регрессии.
13. Как определяется дисперсия остатков? Для каких целей в парной линейной регрессии вычисляется дисперсия остатков?
14. Каким образом выполняется проверка адекватности уравнения регрессии для парной линейной регрессии?
15. Какому закону распределения должна подчиняться случайная величина, чтобы для проверки статистической значимости коэффициентов корреляции и детерминации было бы корректно применять t – статистику Стьюдента и F – статистику Фишера? Укажите смысл статистической значимости коэффициентов корреляции и детерминации.
