12. Оценка влияния отдельных факторов на результирующий фактор y
Факторы, оставленные в модели после устранения мультиколлинеарности, имеют различную степень влияния на наблюдаемый фактор Y, которая оценивается величиной частного коэффициента детерминации: чем больше коэффициент детерминации, тем выше степень влияния.
В ячейках CN25:CO25 указать значения коэффициентов стандартизированной регрессии .
Частные коэффициенты детерминации вычислить в ячейках CN28:CO28 по формулам:
.
Записать индексы факторов, оставшихся в модели после устранения мультиколинеарности.
Проанализировать полученные данные и сделать вывод о том, какой из факторов Xi оказывает наибольшее влияние на результирующий фактор Y. Вывод записать в соответствующем поле шаблона лабораторной работы.
13. Нахождение прогнозного значения фактора y
По построенному уравнению регрессии можно выполнить научно обоснованный и статистически значимый прогноз развития некоторой экономической ситуации. Имея прогнозные значения независимых факторов Xi и используя построенную регрессионную зависимость, можно получить прогноз для наблюдаемого фактора Y.
Сформировать матрицу-строку из прогнозных значений факторов Xi:
.
Значения оставленных в модели прогнозных факторов X i скопировать формулой из ячеек N32:P32 в ячейки CV7:CW7.
В ячейку CU7 занести 1.
Выделить массив из трех заполненных ячеек CU7:CW7 и присвоить ему имя (например, Хр ).
П
рогнозное
значение наблюдаемого фактора
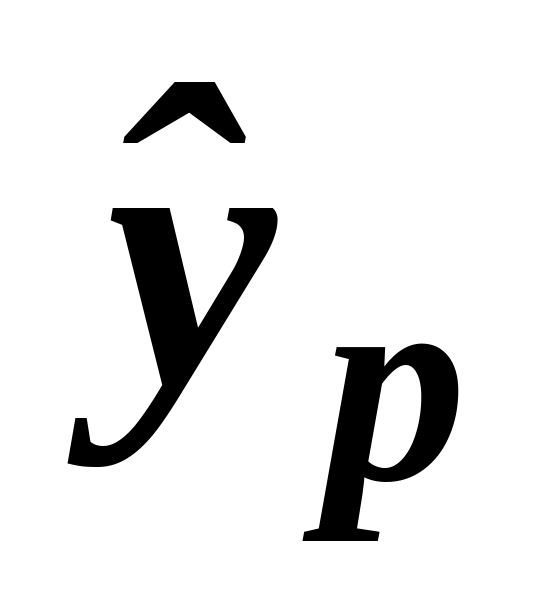вычислить в
ячейке CZ7, используя формулу множественной регрессии
(отброшенный фактор при расчетах в формулу не включать).
Значение
прогноза
записать
в ячейку, предусмотренную шаблоном
лабораторной работы.
14. Построение доверительного интервала для прогноза
Найденное значение прогноза для наблюдаемого фактора является точечной оценкой. Как известно, по точечным оценкам нельзя судить об истинном значении исследуемой величины. В этой связи применяются интервальные оценки, которые с определенной доверительной вероятностью показывают, какому интервалу будет принадлежать истинное значение прогноза. Этот интервал называется доверительным интервалом и определяется формулой:
.
Размах доверительного интервала:
.
По таблицам распределения Стьюдента при = 0,95 и числе
степеней
свободы (n
– 2)
найти значение
и поместить его в ячейку CU10 ( ячейке присвоить имя tg ).
Стандартное отклонение остатков S скопировать (по имени) из
ячейки BS25 в ячейку CW10.
В
ячейке CT
12
запрограммировать
формулу для вычисления
подкоренного выражения:
=1+МУМНОЖ(МУМНОЖ(Xp;МОБР(МУМНОЖ
(ТРАНСП(XX);XX)));ТРАНП(Xp)),
(здесь XX – имя матрицы исходных нестандартизированных данных, столбцы AT6:AV21, Хр – матрица прогнозных значений, использовать имеющиеся в Мастере функций (категория МАТЕМАТИЧЕСКИЕ) операции обращения (МОБР), транспонирования (ТРАНСП) и умножения (МУМНОЖ) матриц).
В ячейке CW12 вычислить размах доверительного интервала для прогноза: tg*S*КОРЕНЬ(CT12).
Значения границ доверительной зоны вычислить
в ячейках CY12 и CA12, выбрав значение из ячейки CZ7.
Таким образом, можно утверждать, что с доверительной вероятностью = 0,95 прогнозное значение фактора Y будет принадлежать полученному статистически обоснованному интервалу.