3. Построение корреляционной матрицы r

Корреляционная матрица определяется по формуле:

.

• Выделить в шаблоне массив ячеек S6:U21 и присвоить ему имя Z.

(Столбец W6:W21 уже имеет имя W ).

• Выделить ячейки AK5:AM7 и разместить в них корреляционную матрицу R (следует использовать имеющиеся в Мастере функций

операции транспонирования и умножения матриц).

Матрице присвоить имя R_{0 .}

• Аналогично в столбце AO5:AO7 разместить матрицу

и присвоить ей имя R_y.

4. Проверка наличия мультиколинеарности

Наиболее полным алгоритмом исследования мультиколлинеарности является алгоритм Фаррара–Глобера. С его помощью тестируют три вида мультиколлинеарности:

• всех факторов ( критерий 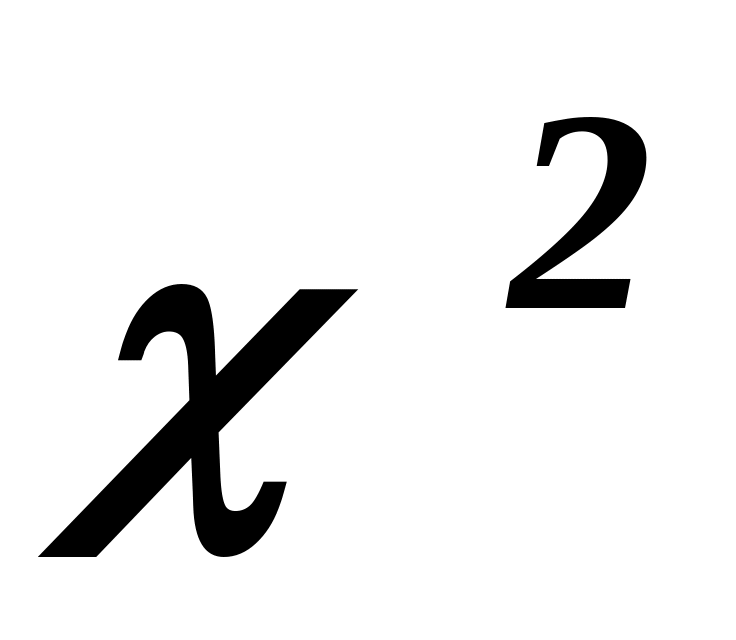–  хи-квадрат);

• каждого фактора с остальными (критерий Фишера);

• каждой пары факторов (критерий Стьюдента).

Для установления наличия мультиколлинеарности определяется значение

,

здесь n – количество наблюдений (объем выборки), m – количество факторов X_i , det (R) – определитель корреляционной матрицы.

Найденное значение сравниваем с критическим значением

, которое выбирается из таблиц критических точек распределения (хи-квадрат) при степенях свободы и уровне значимости .

Критерий Фаррара–Глобера:

Если > , то мультиколлинеарность между наблюдаемыми факторами существует.

• В ячейке AL10 вычислить значение критерия Фаррара–Глобера , при этом значение n взять из ячейки H29, принять m = 3, корреляционную матрицу вызвать по имени R₀ , при вычислении функции ln и определителя матрицы использовать

Мастер функций, категория Математические.

• Используя таблицы критических точек распределения , найти

критическое значение

.

• Поместить найденное значение в ячейку AO10.

Сравнивая полученные значения и , по критерию Фаррара–Глобера сделать вывод о наличии или отсутствии мультиколлинеарности между наблюдаемыми факторами.

Вывод записать в соответствующем поле шаблона лабораторной работы.

5. Выявление факторов, между которыми существует мультиколлинеарность

Чтобы выявить наличие мультиколлинеарности между факторами,

следует воспользоваться критерием Стьюдента:

Критерий Стьюдента:

Если , то между факторами наблюдается мультиколлинеарность, в противном случае мультиколлинеарности нет.

Здесь:

– определяется по таблицам критических точек распределения Стьюдента с доверительной вероятностью = 0,05 и числом степеней свободы (n – m – 1), где n – количество наблюдений (объем выборки), m – количество факторов;

– – наблюдаемое значение критерия Стьюдента, которое находится по формуле:

,

– – частные коэффициенты корреляции.

• Для корреляционной матрицы R найти обратную матрицу R^–1

(Мастер функций, категория Математические, функция МОБР)

и разместить ее в отведенных ячейках AJ18:AL20.

• По значениям элементов обратной матрицы , взятым из ячеек

AO18, AP18 и AP19, вычислить частные коэффициенты корреляции:

.

Н апример, коэффициент ₁₂ вычисляется в ячейке AO18 по формуле:

= − AK18/КОРЕНЬ(AJ18*AK19).

(Достаточно будет вычислить только три коэффициента корреляции, так как матрица R ^–1 симметрична, и ее диагональные элементы равны единице).

• По таблицам критических точек распределения Стьюдента с

доверительной вероятностью = 0,05 и числом степеней свободы

(n – m – 1) найти и записать его значение в ячейку AK26:

.

• По значениям коэффициентов корреляции определить

наблюдаемые значения критерия Стьюдента и записать их в ячейки AK24, AL24, AL25.

Например, в ячейку AK24 запишется формула:

= AO18/ КОРЕНЬ(1−AO18^2)*КОРЕНЬ (n − 4).

• Проанализировать наличие мультиколлинеарности между факторами, используя критерий Стьюдента. Результаты анализа записать в ячейки AO24, AP24, AP25: если мультиколлинеарность есть, то в соответствующую ячейку записывается единица, в случае отсутствия мультиколлинеарности – ноль.

Определить, какой из факторов следует удалить для устранения мультиколлинеарности. Вывод записать в соответствующем поле шаблона лабораторной работы.