
Дифференциальные уравнения
1. Общее решение дифференциального уравнения y’’=-sinx имеет вид…
1) y=sinx+C1+C2 *2) y=sinx+C1x+C2 3) y=cosx+C1 4) y=sinx+C1
2. Общее решение дифференциального уравнения y’’+8y’+16y=0 имеет вид…
1) y=(C1+C2x)e4x 2) y=e-4x(C1 cos(-4x)+C2 sin(-4x))
3) y=e4x(C1 cos4x+C2 sin4x) *4) y=(C1+C2x)e-4x
3. Дифференциальное уравнение ln
ydx-![]() =0
в результате разделения переменных
сводится к уравнению…
=0
в результате разделения переменных
сводится к уравнению…
1) ln ydx=
2)
![]() =dy
*3)
=dy
*3)
![]() =
=![]() 4)
=-
4)
=-
4. Решением дифференциального уравнения y’+10x=0 является функция…
1) y=-10 *2) y=-5x2 3) y=-10x 4) y=5x2
5. Если последовательные значения функции, являющейся решением задачи Коши для дифференциального уравнения y’=ƒ(x,y) с начальными условиями y(x0)=y0, x=x0, находятся по методу Эйлера yk+1=yk+hf(xk,yk), то y1, определяемое уравнением y’=2+x2-y, при y0=3,x0=2 и шаге h=0,2, равно…
1) 3,3 *2) 3,6 3) 3 4) 0,6
6. Если последовательные значения функции, являющейся решением задачи Коши для дифференциального уравнения y’=ƒ(x,y) с начальными условиями y(x0)=y0, x=x0, находятся по методу Эйлера yk+1=yk+hf (xk,yk), то y1, определяемое уравнением y’=y2-x, при y0=3,x0=1 и шаге h=0,1, равно…
1) 0,8 *2) 3,8 3) 3 4) 1,1
7. Общее решение дифференциального уравнения y’’+y’-6y=0 имеет вид…
1) y= e-3x(C1 cos 2x+C2 sin 2x) 2) y= C1e3x+C2e-2x
*3) y= C1e-3x+C2e2x 4) y= e-2x(C1 cos 3x+C2 sin 3x)
8. Дифференциальное уравнение cos4ydx-xdy=0 в результате разделения переменных сводится к уравнению…
1)
![]() 2)
2)
![]() 3) cos4 ydx=xdy
*4)
3) cos4 ydx=xdy
*4)
![]()
9. Решением дифференциального уравнения y’-8x=0 является функция…
1) y=-4x2 *2) y=4x2 3) y=8x 4) y=8
10. Общее решение дифференциального уравнения y’’=5cosx имеет вид…
1) y=5sinx+C1 *2) y=-5cosx+C1x+C2 3) y=-5cosx+C1+C2 4) y=-5cosx+C1
11. Дифференциальное уравнение lnydx-sinxdy=0 в результате разделения переменных сводится к уравнению…
*1)
![]() 2)
2)
![]() 3)
3)
![]() 4) ln ydx=sin
xdy
4) ln ydx=sin
xdy
12. Решением дифференциального уравнения y’-16x=0 является функция…
1) y=16x 2) y=-8x2 *3) y=8x2 4) y=16
13. Общее решение дифференциального уравнения y’’-2y’-3y=0 имеет вид…
1) C1ex+C2e-3x 2) e-3x(C1 cosx+C2 sinx) *3) C1e-x+C2e3x 4) e3x(C1 cos(-x)+C2 sin(-x))
14. Если последовательные значения
функции, являющейся решением задачи
Коши для дифференциального уравнения
y’=ƒ(x,y)
с начальными условиями y(x0)=y0,
x=x0,
находятся по методу Эйлера yk+1=yk+hf
(xk,yk),
то y1, определяемое
уравнением y’=![]() ,
при y0=1,x0=4
и шаге h=0,4, равно…
,
при y0=1,x0=4
и шаге h=0,4, равно…
*1) 2,2 2) 1,2 3) 1 4) 3
15. Общее решение дифференциального
уравнения
![]() имеет вид
имеет вид
*2) 3) 4)
16. Решение дифференциального
уравнения
![]() является функция
является функция
*1)
![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]()
17. Если последовательные значения
функции, являющиеся решением задачи
Коши для дифференциального уравнения
![]() с
начальными условиями
с
начальными условиями
![]() находятся
по методу Эйлера
находятся
по методу Эйлера
![]() определяемое уравнением
определяемое уравнением
![]() при
при
![]() равно
равно
*1) 1,4 2) 0,4 3)1,2 4) 1
18. Дифференциальное уравнении cosydx – e2xdy = 0 в результате разделения переменных сводится к уравнению…
![]() =
dy 2)
=
dy 2)![]() 3) cos y dx = e2xdy
*4)
3) cos y dx = e2xdy
*4)![]()
19. Общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид… y =(C1 +C2x)e7x, тогда корни характеристического уравнения равны…
1) k1= 7,k2 = -7 *2) k1= k2 = 7 3) k1= 7,k2 = 0 4) k1= k2 = -7
20. Общее решение дифференциального
уравнения ![]() =
5x4 имеет вид…
=
5x4 имеет вид…
*1) y =![]() +C1x+C2
2) y= x5+C1
3) y =
+C1
4) y =
+C1+C2
+C1x+C2
2) y= x5+C1
3) y =
+C1
4) y =
+C1+C2
21. Дифференциальное уравнение
(3y2+5)dx-![]() =0
в результате разделения переменных
сводится к уравнению…
=0
в результате разделения переменных
сводится к уравнению…
*1)![]() 2) (3y2+5)
cosxdx =dy 3) (3y2+5)dx
=
4) cosxdx = -
2) (3y2+5)
cosxdx =dy 3) (3y2+5)dx
=
4) cosxdx = -![]()
22.

3 2)
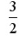 *3)
*3)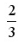 4) -6
4) -6
23.
![]()
1)![]() *2)
*2)
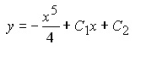 3)
3)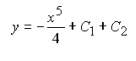 4)
4)![]()
