37

2. Арифметические основы микропроцессорной техники

2.1. Системы счисления

Системой счисления называется совокупность правил записи чисел с помощью символов. Различают непозиционные (римские цифры) и позиционные (десятичная, двоичная и др.) системы счисления. Наиболее часто используются позиционные системы счисления, т.к. они позволяют выполнять арифметические операции.

Каждая позиционная система счисления характеризуется основанием. Основание системы счисления «р»  это количество символов, которое используется для изображения чисел.

В любой позиционной системе счисления целое число может быть представлено в двух формах записи:

1. В виде последовательности символов a_n-1 a_n-2 . . . a₁ a_{0 ,}

2. В виде степенного ряда =

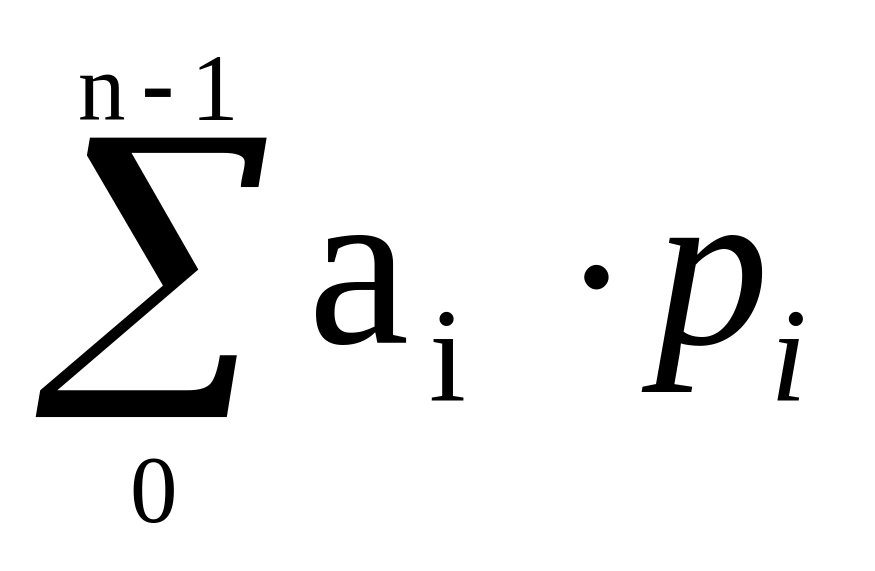= a_n-1р^n-1 + a_n-2р^n-2 + . . . + a₁р¹ + a₀р⁰ = a_n-1q_n-1 + a_n-2q_n-2 + . . . + a₁q₁ + a₀q₀ .

где a_n-1 - символ старшего разряда; a₀ - символ младшего разряда; a_i – символ i-го разряда; i – номер разряда (i = n-1, n-2, … 1, 0); n – количество разрядов числа; р – основание системы счисления; рⁱ = q_i – вес i-го разряда.

В позиционных системах счисления номера символов увеличиваются справа налево от младшего нулевого разряда до старшего (n-1)-разряда. В позиционных системах счисления значение символа зависит от его позиции в числе. Все разряды числа отличаются друг от друга весом или весовым коэффициентом q_i=pⁱ. Веса разрядов увеличиваются справа налево (от младшего к старшему) в «р»-раз.

В человеческой деятельности обычно используется десятичная система счисления.

Десятичная или децимальная (decimal, dec) система счисления имеет основание десять (р=10). Любое число записывается с помощью десяти символов (цифр): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Табл.2.1. Веса разрядов восьмиразрядного десятичного целого числа

Номер разряда	7	6	5	4	3	2	1	0
Вес разряда	107	106	105	104	103	102	101	100
Вес разряда	10000000	1000000	100000	10000	1000	100	10	1

Для отличия одной системы счисления от другой справа пишется символ, равный основанию 125₁₀. Пример записи десятичного числа: 125₁₀.

Пример записи десятичного числа:

• в виде последовательности символов 125;

• в виде степенного ряда 1·10² + 2·10¹ + 5·10⁰ = 100 + 20 + 5.

В вычислительной технике для хранения, обработки и передачи информации (адресов, команд и данных) используется двоичная система счисления.

Двоичная или бинарная (binary, bin) система счисления имеет основание два (р=2). Любое число записывается с помощью двух символов (цифр): 0, 1. Эти двоичные цифры названы битами (bit от binary digit). Для идентификации двоичных чисел используются следующие способы: 1101₂, 1101bin, 1101b, 0b1101.

Табл.2.2. Веса разрядов восьмиразрядного двоичного целого числа

Номер разряда	7	6	5	4	3	2	1	0
Вес разряда	27	26	25	24	23	22	21	20
Вес разряда	128	64	32	16	8	4	2	1

Пример записи двоичного целого числа:

• в виде последовательности символов 111₂;

• в виде степенного ряда 1·(10₂)² + 1·(10₂)¹ + 1·(10₂)⁰ = 100₂ + 10₂ + 1₂ (показатель степени для удобства приведен в десятичной системе счисления).

Цифровая и микропроцессорная техника строится в ИС ТТЛ (интегральные схемы транзисторно-транзисторной логики) и ИС КМОП (интегральные схемы комплементарные-металл-оксидные-полупроводниковые).

Напряжение питания ИС ТТЛ равно Uпит = +5,0 B. Уровни логических сигналов (биты) ИС ТТЛ на физическом уровне представляются напряжением питания Uпит в диапазоне от 0 до +5 В:

1. Биту, имеющему значение ноль (логический ноль, Low), соответствует напряжение низкого уровня U⁰ = (0 … +0,4) В.

2. Биту, имеющему значение единица (логическая единица, High) , соответствует напряжение высокого уровня U¹ = (+2,4 В … +5,0) B.

Для питания различных ИС КМОП могут использоваться напряжения питания Uпит в диапазоне от 3,3 В до +15 В. Уровни логических сигналов (биты) ИС КМОП на физическом уровне представляются напряжением питания Uпит в диапазоне от 0 до + Uпит:

1. Биту, имеющему значение ноль (логический ноль, Low), соответствует напряжение низкого уровня U⁰ = (0 … +0,3∙Uпит) В.

2. Биту, имеющему значение единица (логическая единица, High) , соответствует напряжение высокого уровня U¹ = (+0,99∙Uпит … Uпит) В.

В современных микропроцессорах, построенных на микросхемах КМОП, используется напряжение питания Uпит = 3,3 В и ниже.

Достоинства двоичной системы счисления:

1. Простота технической реализации цифровых элементов, используемых для построения вычислительной системы.

2) Высокая скорость обработки данных.

Недостатки двоичной системы счисления:

1) Трудность запоминания человеком двоичных чисел.

2) Большая разрядность двоичных чисел, по сравнению с другими системами счисления.

Для компактной записи двоичных чисел используются шестнадцатеричные числа.

Шестнадцатеричная или гексадецимальная (hexadecimal) система счисления имеет основание шестнадцать (р=2ⁿ=16, где n = 4 двоичных бита для записи каждого шестнадцатеричного символа). Для записи числа используются шестнадцать символов (цифр и букв): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Значение каждой прописной буквы латинского алфавита буквы A, B, C, D, E, F соответствует десятичным числам 10, 11, 12, 13, 14, 15.

Каждый шестнадцатеричный символ может быть представлен единственным сочетанием четырех бит (тетрадой). Тетрада может принимать 2⁴=16 значений (от 0₁₀ до 15₁₀ или от 0₁₆ до F₁₆). Шестнадцатеричная система используется для кодирования двоичных чисел, разрядность которых кратна четырем (4, 8, 16 и т.д.). Пример записи шестнадцатеричного числа: А5₁₆, А5hex, А5h, $А5, 0xА5.

Табл.2.4. Веса разрядов восьмиразрядного шестнадцатеричного целого числа

Номер разряда	7	6	5	4	3	2	1	0
Вес разряда	167	166	165	164	163	162	161	160
Вес разряда	268435456	16777216	1048576	65536	4096	256	16	1

В таблице 2.5 представлены последовательности целых чисел, записанных в различных системах счисления.

Табл.2.5. Последовательности целых чисел в разных системах счисления

Dec	Bin	Hex	Dec	Bin	Hex	Dec	Bin	Hex	Dec	Bin	Hex
0 1 2 3	0000 0001 0010 0011	0 1 2 3	4 5 6 7	0100 0101 0110 0111	4 5 6 7	8 9 10 11	1000 1001 1010 1011	8 9 A В	12 13 14 15	1100 1101 1110 1111	C D E F

Шестнадцатеричные числа имеют следующие преимущества перед двоичными и десятичными:

1. Шестнадцатеричное число дает более компактную запись двоичного числа.

2. Шестнадцатеричное число имеет более упорядоченную форму записи по сравнению с десятичным числом, способствующую лучшему запоминанию.

Табл.2.6. Сравнительная характеристика различных систем счисления

Разрядность двоичного числа, n	Максимальное значение n-разрядного числа (2n-1)
	Двоичное	Десятичное	Шестнадцатеричное
4	1111	15	F
8	1111 1111	255	FF
12	1111 1111 1111	4095	FFF
16	1111 1111 1111 1111	65535	FFFF
20	1111 1111 1111 1111 1111	1048575	FFFFF

В любой позиционной системе счисления вещественное число может быть представлено в двух формах записи:

1. В виде последовательности символов a_n-1 a_n-2 . . . a₁ a₀ , a_-1 a_-2 …a_-(m-1) a_-m,

2. В виде степенного ряда =

= a_n-1р^n-1 + a_n-2р^n-2 + . . . + a₁р¹ + a₀р⁰ + a_-1р^-1 + a_-2р^-2 + … + a_-(m-1)р^-(m-1) + a_-mр^{-m =}

= a_n-1q_n-1 + a_n-2q_n-2 + . . . + a₁q₁ + a₀q₀ + a_-1q_-1 + a_-2q_-2 + … + a_-(m-1)q_-(m-1) + a_-mq_-m .

где a_i – значение символа i-го разряда; i – номер разряда (i = n-1, n-2, … 1, 0, -1, -2 …, -m+1, -m); р – основание системы счисления; q_i – вес i-го разряда (q_i=рⁱ); n – количество разрядов целой части вещественного числа; m – количество разрядов дробной части вещественного числа.

Пример записи десятичного вещественного числа:

• в виде последовательности символов 125,875₁₀;

• в виде степенного ряда

1·10² + 2·10¹ + 5·10⁰ + 8·10^-1 + 7·10^-2 + 5·10^-3 = 100₁₀ + 20₁₀ + 5₁₀ + 0,8₁₀ + 0,07₁₀. + 0,005₁₀

Табл.2.7. Веса разрядов восьмиразрядного десятичного дробного числа

Номер разряда	-1	-2	-3	-4	-5	-6	-7	-8
Вес разряда	10-1	10-2	10-3	10-4	10-5	10-6	10-7	10-8
Вес разряда	0,1	0,01	0,001	0,0001	0,00001	0,000001	0,0000001	0,00000001

Пример записи двоичного вещественного числа:

• в виде последовательности символов 1111101,111₂;

• в виде степенного ряда

1·(10₂)⁶ + 1·(10₂)⁵ + 1·(10₂)⁴ + 1·(10₂)³ + 1·(10₂)² + 0·(10₂)¹ + 1·(10₂)⁰ + 1·(10₂)^-1 + 1·(10₂)^-2 + 1·(10₂)^-2 =

1000000₂ + 100000₂ + 10000₂ + 1000₂ + 100₂ + 0₂ + 1₂ + 0,1₂ + 0,01₂ + 0,001₂

(показатель степени для удобства приведен в десятичной системе счисления).

Табл.2.8. Веса разрядов восьмиразрядного двоичного дробного числа

Номер разряда	-1	-2	-3	-4	-5	-6	-7	-8
Вес разряда	2-1	2-2	2-3	2-4	2-5	2-6	2-7	2-8
Вес разряда	1/2	1/4	1/8	1/16	1/32	1/64	1/128	1/256