27.Точки разрыва функции и их классификация. Примеры: ф-ия Дирихле и другие примеры

О 1. Пусть ф-ия определена на мн-ве и . Если ф-ия непрерывна в точке , то она наз. точкой непрерывности функции . В противном случае, точка наз. точкой разрыва функции .О 2. Пусть – точка разрыва функции . Если оба односторонних предела и существуют и конечны, то она наз. точкой разрыва 1-го рода

О 3. Точка разрыва 1-го рода наз. точкой устранимого разрыва функции , если в ней существует предел функции , но он не равен ее значению в этой точке.О 4. Точка разрыва функции наз. точкой разрыва 2-го рода, если она не явл. точкой разрыва 1-го рода.

Пример 1 (всюду разрывной функции). Ф-ия Дирихле, определенная на всей числовой оси равенствами:

явл. разрывной в каждой точке . Действительно, для любой последовательности рациональных чисел , сходящейся к точке , имеем , а для любой последовательности иррациональных чисел , , в свою очередь, имеем . Следовательно, ни в одной точке не существует предел , т.е. каждая точка – точка разрыва функции Дирихле.

Более того, нетрудно видеть, что ни в одной точке не существует ни один из односторонних придела и , так как описанные выше последовательности и , с одной стороны, можно выбрать так, что , а с другой стороны, можно выбрать и так, что . Таким образом, каждая точка – точка разрыва 2-го рода функции Дирихле.

Пример 2. Ф-ия «сигнум » очевидно, разрывна в точке , причем эта точка – точка разрыва 1-го рода.

Пример 3. Ф-ия разрывна в точке , которая, очевидно, явл. точкой устранимого разрыва.

28.Равномерно непрерывные функции. Теорема Кантора.

О 1. Ф-ия наз. непрерывной на мн-ве , если она непрерывна в каждой точке .

О 2. Ф-ия наз. равномерно непрерывной на мн-ве , если для любого такое, что , удовлетворяющих неравенству

(1) имеет место неравенство . (2)

Теорема 1 (Кантора). Непрерывная на отрезке ф-ия равномерно непрерывна на этом отрезке.

29.Теоремы Больцано-Коши о промежуточных значениях непрерывной функции. Теорема 1 (первая теорема Больцано-Коши)

Пусть ф-ия определена и непрерывна на отрезке ( ) и на концах его принимает значения разных знаков ( ). Тогда найдется такая точка , в которой ф-ия обращается в нуль: (1)

Д о к а з а т е л ь с т в о. Для определенности будем считать, что (2)

Разделим отрезок на два средней его точкой . Тогда либо в этой точке имеет место равенство (1), либо на концах одного (и только одного) из отрезков

, , (3)

ф-ия будет принимать значения разных знаков, причем, в силу (2), отрицательное значение – на левом конце и положительное – на правом. В случае реализации второй из указанных возможностей обозначим тот из отрезков (3), на концах которого ф-ия принимает значения разных знаков, через . Таким образом, будем иметь:

. (4)

Разделим теперь пополам отрезок . Тогда опять-таки, либо в точке имеет место равенство (1), либо на концах одной из половин отрезка ф-ия принимает значения разных знаков. При реализации второй из этих возможностей обозначим через ту из этих половин, для которой

(5)

Продолжая описанный процесс деления отрезков пополам и далее, либо через конечное число шагов мы обнаружим, что в точке деления очередного отрезка ф-ия обращается в нуль и тем самым завершим доказательство теоремы, либо получим бесконечную последовательность вложенных друг в друга отрезков , длины которых стремятся к нулю при , (6)

при этом на концах каждого из этих отрезков ф-ия принимает значения разных знаков, а именно, (7)

По лемме о вложенных отрезках рассматриваемые отрезки имеют единственную общую точку , при этом (8)

Тогда переходя в неравенствах (7) к пределу при , с учетом непрерывности функции на отрезке и, в частности, непрерывности ее в точке , получим

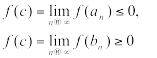
и, следовательно, , причем из неравенств (2) следует, что □Теорема 2 (вторая теорема Больцано-Коши)

Пусть ф-ия определена и непрерывна на отрезке , причем на концах этого отрезка она принимает разные значения .

Тогда каковы бы ни было число , лежащее м/д и найдется такое , что

.

Д о к а з а т е л ь с т в о. Пусть для определенности . Выберем произвольное , , и рассмотрим вспомогательную ф-ию . Она, очевидно, непрерывна на отрезке и на его концах принимает значения разных знаков:

.

По теореме 1 существует такое , что , т.е. или □