Приклади

1. Використовуючи означення похідної функції f у точці, знайти похідні функцій:

а) ; б) .

Розв’язання. а) Нехай х – довільна фіксована точка з D(f)=R.

1. Надамо х приросту х і знайдемо відповідний приріст функції f(x):

f(x)=f(x+х)–f(x)=sin(х+х)–sin x= .

При перетворенні різниці синусів у добуток тригонометричних функцій використано формулу .

2. = .

3. Знайдемо :

= =

= .

При знаходженні використано першу чудову границю: .

Оскільки х – довільна точка, то = для всіх хR.

Отже, .

б) Нехай х – довільна фіксована точка з D(f)=R.

1. Надамо х приросту х і знайдемо відповідний приріст функції f(x):

f(x)=f(x+х)–f(x)= = .

2. = .

3. Знайдемо :

= .

При знаходженні використано важливу границю: .

Внаслідок довільності аргумента х, маємо: = для всіх хR.

Отже, .

2. Довести, що у точці х₀=0 не існує похідна функції .

Розв’язання. Знайдемо ліву і праву похідні функції у точці х₀=0:

= = =

= = = ;

= = = .

Оскільки ліва і права похідні функції у точці х₀=0 не дорівнюють одна одній, то в цій точці не існує похідна функції f.

3. Знайти похідні функцій:

а) y=sin x+x⁸–2; б) + ; в) y= x⁵lnx; г) y= ;

д) y=ln(cos x); е) y=arctg x⁴; є) y= ; ж) , x>0.

Розв’язання. а) Спочатку використаємо правило 1, а потім формули 5, 2, 1 із таблиці похідних:

= – =cos x+8x⁷–0= =cos x+8x⁷.

б) Спочатку використаємо правило 1, а потім правило 2.1 та формули 7, 2.1, 2.3, 1 із таблиці похідних:

= =

= = = .

в) Спочатку використаємо правило 2, а потім формули 2, 4.1 із таблиці похідних:

= =5x⁴lnx+x⁵ =5x⁴lnx+x⁴= .

г) Використаємо правило 3, а потім формули 10, 2 із таблиці похідних:

= =

= = .

д) Функція y=ln(cos x) є складеною. Її можна записати у вигляді y=ln u, де u=cos x. Для знаходження похідної функції y=ln(cos x) спочатку скористаємося правилом 4: , де u=g(x), а потім формулами 4.1, 6 із таблиці похідних. Отже,

.

е) Функція y=arctg x⁴ – складена; u=x⁴ – внутрішня функція, y=arctg u – зовнішня функція. Для знаходження похідної функції y=arctg x⁴ використаємо правило 4 і формули 11, 2 з таблиці похідних:

=

= .

При знаходженні похідної складеної функції проміжні етапи, що пов’язані із виділенням внутрішньої і зовнішньої функцій, із знаходженням похідної зовнішньої функції, як правило, не записують у розв’язанні. У цьому разі розв’язання цього завдання буде таким:

= .

є) Для знаходження похідної функції y= спочатку використаємо правило 2, потім правило 4 (для знаходження похідної складеної функції ) і формули 7, 2.3 з таблиці похідних:

= =

= = .

ж) Функції (x>0) є степенево-показниковою. Тому за правилом 6 маємо:

, x>0.

4. Знайти значення похідної функції у точці х₀=0,6.

Розв’язання. Спочатку знайдемо похідну функції f. При знаходженні похідної функції врахуємо, що ця функція є складеною.

Отже,

= =

= .

Тоді .

5. Знайти рівняння дотичної, проведеної до графіка функції у точці з абсцисою х₀=–2.

Розв’язання. Використаємо рівняння дотичної, проведеної до графіка функції f у точці з абсцисою х₀: .

Щоб записати це рівняння знайдемо і :

;

;

.

Тоді

= = .

Отже, – шукане рівняння дотичної.

6. Знайти рівняння дотичної до графіка функції , яка паралельна до прямої .

Розв’язання. Виходячи з геометричного змісту похідної, кутовий коефіцієнт дотичної, проведеної до графіка функції , дорівнює . Оскільки шукана дотична є паралельною до прямої , то кутові коефіцієнти цих прямих є однаковими. Враховуючи, що кутовий коефіцієнт k прямої дорівнює –2, маємо:

   х=1.

Отже, якщо до графіка функції f у точці з абсцисою х₀=1 провести дотичну, то вона буде паралельною до прямої . Знайдемо рівняння цієї дотичної.

;

;

= .

Отже, – шукане рівняння дотичної.

7. Матеріальна точка рухається прямолінійно за законом .

а) Знайти швидкість і прискорення точки у момент часу (шлях s вимірюється в метрах).

б) Через скільки секунд після початку руху точка зупиниться?

Розв’язання. а) Враховуючи механічний зміст похідної, знайдемо за яким законом змінюється швидкість і прискорення точки:

;

.

Тоді швидкість і прискорення точки у момент часу є такими:

м/с; м/с².

Від’ємне значення прискорення вказує на сповільнений рух точки.

б) Якщо точка зупинилася, то її швидкість дорівнює нулю. Тому щоб знайти момент часу, коли точка зупиниться, потрібно розв’язати рівняння :

 

За змістом задачі від’ємне значення t не підходить. Отже, через 5 с після початку руху точка зупиниться.

8. Обсяг продукції, виробленої бригадою робітників, описується функцією (одиниць), , де t – робочий час у годинах. Визначити продуктивність праці 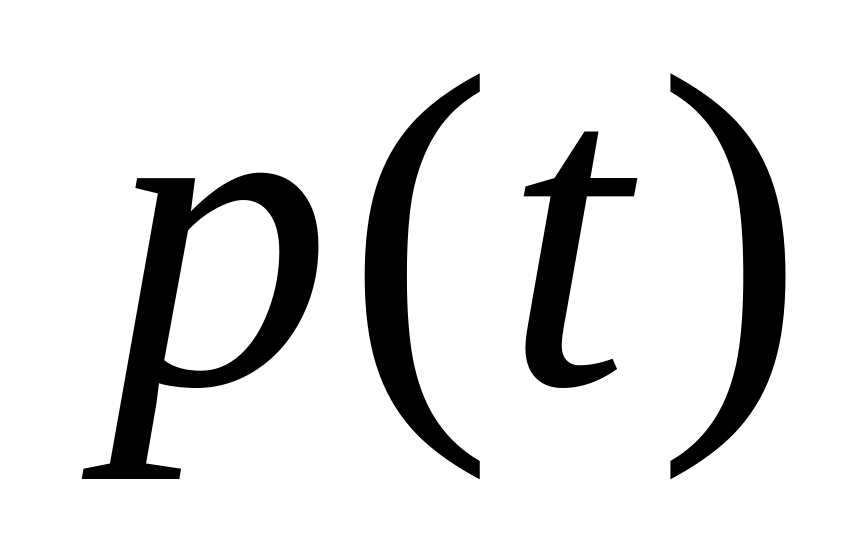через годину після початку роботи та за годину до її закінчення.

Розв’язання. Враховуючи економічний зміст похідної, знайдемо закон, за яким змінюється продуктивність праці бригади робітників:

= .

У задані моменти часу t₁=1 год і t₂=8–1=7 год відповідно маємо таку продуктивність праці бригади робітників:

(одиниць/год);

(одиниць/год).

Як бачимо, наприкінці роботи продуктивність праці бригади робітників зменшується.