Завдання для самостійного розв’язування
Дослідити
функцію f
і побудувати її графік:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
.
В
ідповіді:
D(f)=R;
– інтервал неперервності, точок розриву
функція не має; асимптот не має; (0;0) і
(3;0) – точки перетину графіка з осями
координат; інтервали спадання: (–;0)
і (2;+),
інтервал зростання: (0;2), xmin=0,
ymin=0,
xmax=2,
ymax=4;
(–;1)
– інтервал опуклості вниз, (1;+)
– інтервал опуклості вгору, хперег.=1,
yперег.=2;
,
.
2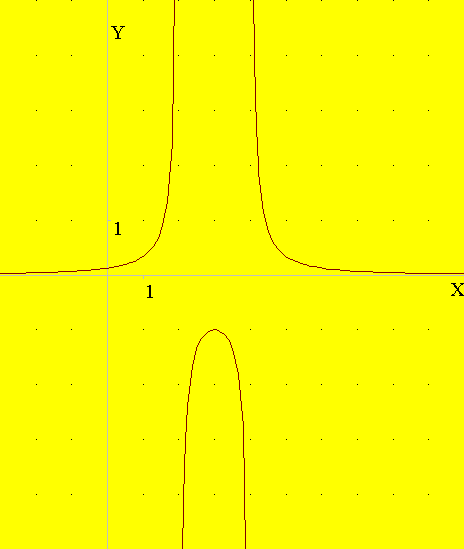
)
D(f)=R\{2; 4};
(–;2),
(2;4), (4;+)
– інтервали неперервності, х=2
і х=4
– точки розриву; х=2
і х=4
– вертикальні асимптоти, y=0
– горизонтальна асимптота;
– точка перетину графіка з віссю ординат;
інтервали спадання: (3;4) і (4;+),
інтервали зростання: (–;2)
і (2;3), xmax=3,
ymax=–1;
(–;2)
і (4;+)
– інтервали опуклості вниз, (2;4) –
інтервал опуклості вгору, точок перегину
немає;
,
,
,
,
,
.
3) D(f)=R\{1};
(–;1)
і (1;+)
– інтервали неперервності, х=1
– точка розриву; х=1
– вертикальна асимптоти; (0;0) – точка
перетину графіка з осями координат;
інтервали спадання: (–;1)
і (1;1,5), інтервал зростання: (1,5;+),
xmin=1,5,
ymin=6,75;
(–;0)
і (1;+)–
інтервали опуклості вниз, (0;1) – інтервал
опуклості вгору, хперег.=0,
yперег.=0;
,
,
,
.
4
)
D(f)=R;
– інтервал неперервності, точок розриву
функція не має; y=0
– горизонтальна асимптота; (0;–2) і
(1;0) – точки перетину графіка з осями
координат; інтервали спадання: (–;–1)
і (3;+),
інтервал зростання: (–1;3), xmin=–1,
ymin=–3,
xmax=3,
ymax=1;
,
.
5
)
D(f)=R\{0};
(–;0)
і (0;+)
– інтервали неперервності, х=0
– точка розриву; х=0
– вертикальна асимптоти; графік не
перетинає осі координат; інтервали
спадання: (–;0)
і (0;0,5), інтервал зростання: (0,5;+),
xmin=0,5,
ymin=
;
(–;0)
і (0;+)
– інтервали опуклості вниз, точок
перегину немає;
,
,
,
.
6
)
D(f)=(0;+);
(0;+)
– інтервал неперервності, точок розриву
функція не має; асимптот графік не має;
(1;0) – точка перетину графіка з віссю
абсцис; інтервал спадання:
,
інтервал зростання:
,
xmin=
,
ymin=
;
(0;+)
– інтервали опуклості вниз, точок
перегину немає;
,
.