Модуль іv. Похідна функції Заняття 12

§4.1. Похідна функції. Правила диференціювання функцій. Похідні основних елементарних функцій

Нехай функція y=f(x) визначена в деякому околі точки х₀. Надамо х₀ приросту х і розглянемо відповідний приріст функції f(x₀)=f(x₀+х)–f(x₀).

Похідною функції y=f(x) у точці х₀ називають границю відношення приросту f(x₀) функції до приросту х аргументу, коли приріст аргументу х прямує до нуля. Позначають або .

Отже, за означенням: = .

Якщо =, то кажуть, що функції f у точці х₀ має нескінченну похідну.

Для знаходження похідної функції f у точці х₀ за означенням потрібно виконати такі кроки:

Надати аргументу х₀ приросту х і знайти відповідний приріст функції f(x₀)=f(x₀+х)–f(x₀).
Скласти відношення .
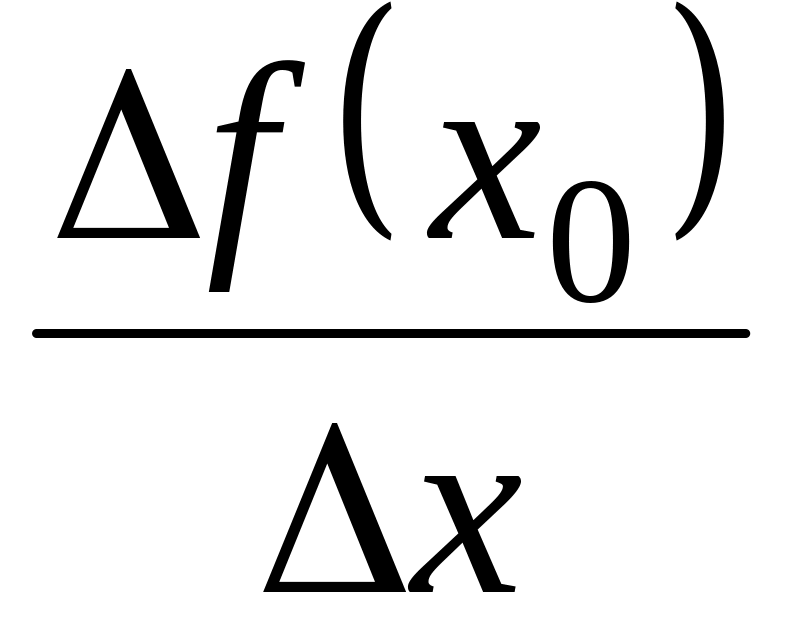Знайти 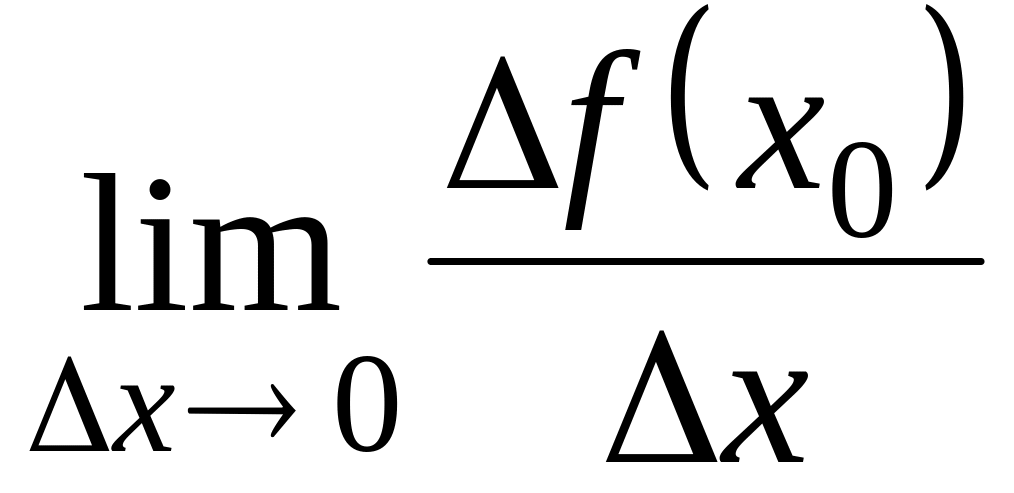. Якщо ця границя існує, то вона є похідною функції f у точці х₀, тобто = .

Нехай функція y=f(x) визначена на півінтервалі (на піввідрізку ). Вважають, що функція f у точці х₀ має ліву (праву) похідну, якщо в цій точці існує ліва (права) границя:

Для того щоб у точці х₀ існувала похідна , необхідно й достатньо, щоб у цій точці існувала ліва і права похідні цієї функції і щоб ліва похідна дорівнювала правій похідній.

Функцію, що має скінченну похідну в точці х₀, називають диференційовною в цій точці. Якщо функція диференційовна в точці х₀, то вона є неперервною в цій точці.

Нехай D₁ – множина точок, у яких функція f диференційовна. Поставивши у відповідність кожному числу хD₁ число , одержимо нову функцію з областю визначення D₁. Цю функцію називають похідною функції y=f(x) і позначають або , або .

Операцію відшукання похідної функції називають диференціюванням функції.

Г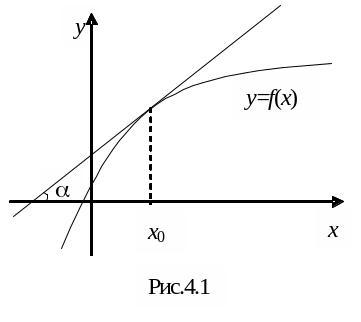 еометричний зміст похідної: дорівнює кутовому коефіцієнту k дотичної, проведеної до графіка функції f у точці з абсцисою х₀, тобто =tg , де  – кут між дотичною і додатним напрямом осі абсцис (рис.4.1).

Існування похідної функції f у точці х₀ рівносильне існуванню дотичної, проведеної до графіка функції f у точці з абсцисою х₀.

Рівняння дотичної, проведеної до графіка функції f у точці з абсцисою х₀: .

Механічний зміст похідної: якщо матеріальна точка рухається за законом , то дорівнює швидкості точки в момент часу , тобто ; якщо матеріальна точка рухається із швидкістю, що змінюється за законом , то дорівнює прискоренню точки в момент часу , тобто .

Економічний зміст похідної: якщо – кількість виробленої виробником продукції за час t, то дорівнює продуктивності праці виробника в момент часу , тобто .