1.4. Концентрації носіїв заряду

Утворення вільних носіїв заряду потребує витрат енергії на подолання енергетичних щілин між дозволеними зонами або між локальними рівнями та цими зонами (рис. 1.7). У звичайних умовах енергія, необхідна для утворення вільних носіїв, береться з запасу теплової енергії кристала. Процес утворення вільних носіїв у цьому випадку називають термічною іонізацією атомів напівпровідника.

Внаслідок сильної взаємодії між вільними електронами й атомами або іонами кристала температури кристалічної гратки та вільних електронів, утворених у процесі термічної іонізації, у звичайних умовах практично однакові. Тому такі носії заряду перебувають у стані термодинамічної рівноваги з граткою.

- 11 -

Вільні носії заряду, що утворюються внаслідок термічної іонізації атомів кристала і перебувають в стані термодинамічної рівноваги з кристалічною граткою, називають рівноважними носіями.

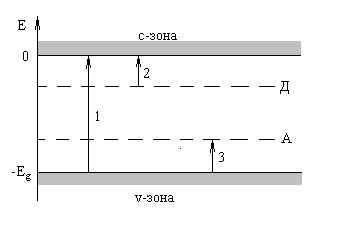
Рис. 1.7. Схема можливих електронних переходів у процесі іонізації

основних (перехід 1) та домішкових (переходи 2 і 3) атомів.

Через А і Д позначені локальні рівні акцепторних та донорних

домішкових центрів відповідно

Концентрації рівноважних електронів у зоні провідності (с-зона) й дірок у валентній зоні (v-зона), які позначимо через n_о і p_о відповідно, дорівнюють:

, (1.3)

, (1.4)

де N_c i N_v – ефективні густини електронних станів у с- і v-зоні відповідно; F – рівень Фермі; k = 6,625^.10^-34 Дж ^. с – стала Больцмана.

Ефективні густини станів N_c i N_v відповідно дорівнюють

, (1.5)

, (1.6)

де – ефективні маси електронів і дірок. Із формул (1.3) і (1.4) видно, що концентрації електронів у зоні провідності та дірок у валентній зоні збільшуються при підвищенні температури напівпровідника.

- 12 -

Для напівпровідникового кристала без домішок і власних точкових дефектів

. (1.7)

Величину n_i називають власною концентрацією носіїв заряду або концентрацією носіїв заряду в напівпровіднику з власною електропровідністю. У такому напівпровіднику вільні електрони і дірки утворюються внаслідок іонізації атомів напівпровідника, тобто внаслідок переходів електронів із v-зони в с-зону (рис. 1.7, переходи 1). У легованих напівпровідниках концентрація електронів у зоні провідності не дорівнює концентрації дірок у валентній зоні ( ). У напівпровіднику n-типу , а в напівпровіднику р-типу .

Використовуючи вирази (1.3) і (1.4), можна отримати

. (1.8)

Співвідношення (1.8) виконується не лише для напівпровідника з власною провідністю, в якому , але й для домішкових напівпровідників. Для будь-якого напівпровідника виконується рівність

. (1.9)

Зі співвідношення (1.9) випливає, що при заданій температурі добуток концентрацій електронів та дірок у невиродженому напівпровіднику є сталою величиною, яка залежить лише від властивостей напівпровідника (через величини E_g,  ). За аналогією з хімічною термодинамікою співвідношення (1.9) називають законом чинних мас. Згідно з названим законом збільшення концентрації одного з носіїв заряду зменшує кількість носіїв протилежного знака так, що їх добуток залишається сталим.

Використовуючи вираз (1.9), завжди можна обчислити концентрацію одного з носіїв заряду при заданій температурі, якщо відома концентрація носіїв протилежного знака.