§5 Условная вероятность события

Пусть - вероятностное пространство (дискретное) и произвольное событие из , удовлетворяющее условию . Определим на функцию следующим образом: .

Легко убедиться, что функция является вероятностью на пространстве . Действительно, первое условие определение вероятности – условие неотрицательности, очевидно, выполняется. Далее, поскольку , то и второе условие определения вероятности у нас выполняется.

Определение 1. Функция называется условной вероятностью на , индуцированной событием В.

Определение 2. Условной вероятностью события относительно события называется число .

Основные свойства условной вероятности:

1. .

Действительно, так как при , то .

2. .

3. .

4. 

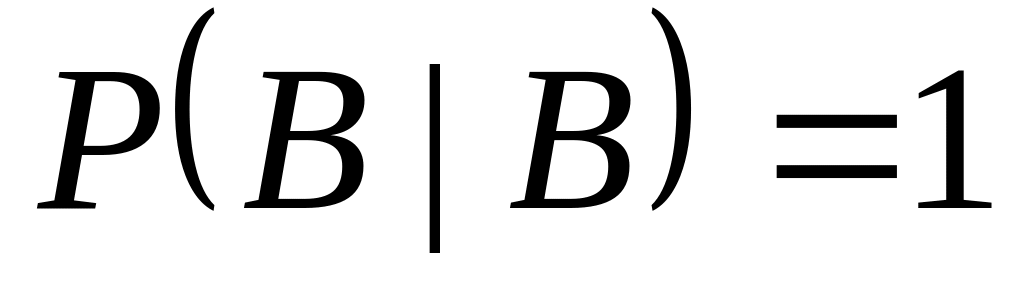Предположим, что элементарные события равновозможны. Тогда в силу свойства1. . Отсюда следует, что условная вероятность представляет собой вероятность события , вычисленную при дополнительном предположении, что произойдет событие В.

Примет 1. Брошены две игральные кости. Требуется определить вероятность того, что сумма выпавших на них очков равна 8 (событие А), если известно, что эта сумма есть четное число (событие В).

Число всех исходов равно 36. Число исходов, благоприятствующих событию А равно 5. Так как i+j=8 удовлетворяется при i=2, 3, 4, 5, 6 и j=6, 5, 4, 3, 2. Следовательно, вероятность события А равна . Вычислим теперь вероятность . Так как число исходов (i, j) с четной суммой i+j=18, то .

Пример 2. Из колоды карт последовательно вынуты две карты. Найти вероятность того, что вторая карта будет тузом, если первоначально был вынут туз.

Обозначим {первоначально был вынут туз},

{вторая карта является тузом}.

.

Пример 3. Вероятность попасть в самолет равна 0,4, а вероятность его сбить равна 0,1. Найти вероятность того, что при попадении в самолет он будет сбит.

Обозначим {попадение в самолет},

{самолет сбит }.

Тогда, так как , то . Следовательно, .

Теорема умножения вероятностей.

Теорема. Вероятность произведения двух событий А и В равна произведению вероятности одного из событий на условную вероятность другого, при условии, что первое произошло:

.

Эта теорема непосредственно вытекает из свойства 1 условной вероятности.

Определение 2. Событие А независимо от события В, если .

Если А независимо от события В, то В независимо от А, и, следовательно, свойство независимости событий взаимно. Действительно, А независимо от В. Тогда

, т.е. В независимо от А.

Пусть события А и В независимы, тогда в силу формулы (1) имеем. , т.е. вероятность произведения двух независимых событий равна произведению их вероятностей.

Свойства независимых событий

1º. Если события А и В независимы, то , обратно, если Если А и В удовлетворяют условию и , то А не зависит от В.

2º. Если А и В независимы, то независимы события и В, и Аи и .

3º. Если = , то А и В независимы и наоборот.

Определение 3. События А и В называются независимыми, если .

События (k≥2) называются попарно независимыми, если , при i j.

Определение 4. События (k≥2) называются независимыми в совокупности, если для любой последовательности событий имеет место равенство .

Формула умножения вероятностей для нескольких событий

Для любой последовательности событий справедлива формула при условии, что .

Пример. Из колоды карт последовательно без возвращения вытаскиваются 3 карты. Какова вероятность того, что все три карты тузы.

Обозначим А={первая карта туз},

B={вторая карта туз},

С={третья карта туз}.

Тогда .