
- •Предмет теории вероятностей
- •§1. События и операции над ними
- •§ 2. Определение вероятности
- •§ 3. Классическое определение вероятности
- •§ 4. Основные свойства вероятностей
- •§5 Условная вероятность события
- •§6. Формула полной вероятности и формула Байеса
- •§ 7. Геометрическая вероятность
- •§2. Случайные величины
- •§3. Числовые характеристики дискретных случайных величин
- •§4. Основные законы распределения дискретных случайных величин.
- •Функция распределения случайной величины
- •Свойства функции распределения
Литература
Гмурман В.С. (Владимир Ефимович) Теория вероятностей и математическая статистика. Руководство к решению задач по теории вероятностей и математической статистике.
Вентцель Е.С. Теория вероятностей.
Кремер Н.Ш. (Наум Шевелевич) Теория вероятностей и математическая статистика.
Гнеденко Б.В. (Борис Владимирович) Курс теории вероятностей.
Бочаров В.В. Теория вероятностей и математическая статистика.
Предмет теории вероятностей
Теория вероятностей есть наука, изучающая закономерности в случайных явлениях
Случайное явление –это такое явление, которое при неоднократном воспроизведении одного и того же опыта протекает каждый раз несколько по –иному.
Пример 1. Производится стрельба из орудия. Пользуясь методами внешней баллистики, можно найти теоретическую траекторию снаряда. Эта траектория вполне определяется условиями стрельбы: начальная скорость снаряда, угол бросания снаряда. Если произвести несколько выстрелов при неизменных основных условиях , мы получим не одну теоретическую траекторию, а целый пучок траекторий, образующих «рассеивание снарядов». Фактическая траектория каждого из снаряда неизбежно отклоняется от теоретической за счет влияния совокупности факторов: метеорологические, отклонение веса снаряда от номинала и т. д.
Пример 2. Одно и то же тело взвешивается несколько раз на аналитических весах. Результаты повторных взвешиваний несколько отличаются друг от друга. Это различие обусловлено влиянием второстепенных факторов.
В природе нет ни одного физического явления, в котором не присутствовало бы в той или иной мере элементы случайности. Как бы точно и подробно ни были фиксированы условия опыта, невозможно достигнуть того, чтобы при повторении опыта результаты полностью и в точности совпадали.
Существуют два подхода к изучению этих явлений. Один из них состоит в том, что выделяются основные решающие факторы, а влиянием остальных, второстепенных факторов просто пренебрегают. Такая схема изучения явлений постоянно применяется в технике, физике, механике. При исследовании многих явлений (прежде всего социально-экономических) такой подход неприемлем. В этих явлениях необходимо учитывать не только основные, но и второстепенные факторы, приводящие к случайным искажениям результата, т.е. вносящих в него элемент неопределенности. Элемент неопределенности требует создания специальных методов для изучения таких явлений. Такие методы разрабатываются в теории вероятностей.
§1. События и операции над ними
Теория вероятностей
– это раздел математики, в котором
изучаются теоретические модели опытов
со случайными исходами. Эти опыты
полностью характеризуются наборами
всех возможных их исходов
![]() .
Понятие исхода опыта является первичными
и не определяется. Множество всех исходов
данного опыта мы будем обозначать буквой
.
Понятие исхода опыта является первичными
и не определяется. Множество всех исходов
данного опыта мы будем обозначать буквой
![]() :
:
![]() .
.
Определение1. Любое подмножество множества называется событием.
Само множество
при этом называется достоверным событием
и его пустое подмножество
![]() называется невозможным событием.
называется невозможным событием.
Пример А={Выпадение не более шести очков при бросании одной игральной кости}- достоверное событие.
В={Появление 12 очков при бросании одной игральной кости}-невозможное событие.
Если исход
![]() принадлежи событию А,
то мы будем говорить также, что исход
благоприятствует
событию А.
Согласно данному определению все исходы
принадлежи событию А,
то мы будем говорить также, что исход
благоприятствует
событию А.
Согласно данному определению все исходы
![]() являются элементарными событиями, а
все множество -
пространством элементарных событий.
являются элементарными событиями, а
все множество -
пространством элементарных событий.
Пример 1. При бросании монеты возможны 2 элементарных исходов (событий):
![]()
![]() - выпадение орла
- выпадение орла
![]() -
выпадение решки,
-
выпадение решки,
т.е. пространство
элементарных событий
![]()
Пример 2.
При бросании игральной кости возможны
следующие элементарные исходы:
- выпадение 1 очка,
-
выпадение 2 очков,
- выпадение i-очков,
![]() -
выпадение 6 очков. Т.е. пространство
элементарных событий
-
выпадение 6 очков. Т.е. пространство
элементарных событий
![]() .
Событие А,
состоящее в выпадении четного числа
очков есть
.
Событие А,
состоящее в выпадении четного числа
очков есть
![]() .
.
Определение 2.
Событие А
влечет за собой событие В,
если всякий исход, принадлежащий событию
А,
принадлежит и событию В
и пишут
![]() .
.
Определение 3. Два события А и В называются равными, если они состоят из одних и тех же исходов. А=В.
Определение 4.
Событие
![]() ,
состоящее из всех исходов
,
не принадлежащих событию А, называется
противоположным событию А.
,
состоящее из всех исходов
,
не принадлежащих событию А, называется
противоположным событию А.
Определение 5.
Суммой двух
событий А и
В
называется событие, состоящее из исходов
принадлежащих либо событию А
либо событию В,
обозначается таким образом:
![]() .
- (Появление хотя бы одного из этих
событий А и В).
.
- (Появление хотя бы одного из этих
событий А и В).
Пример1. Опыт состоит в пяти выстрелах по мишени. Тогда могут произойти следующие события:
А0- ни одно попадание; А1 – ровно одно попадание; А2 – ровно два попадания;
А3 – ровно три попадания; А4 – ровно четыре попадания; А5 – ровно пять попаданий;
А = А0+ А1+ А2- есть событие «не более двух попаданий»;
В= А3+ А4+ А5 – есть событие «не менее трех попаданий».
Пример2. А – попадание в цель при первом выстреле; В – попадание в цель при втором выстреле, тогда А+В – попадание в цель вообще, безразлично при каком выстреле.
Определение 6.
Разностью
двух событий А
и В
называется событие, состоящее из всех
исходов принадлежащих событию А
и не принадлежащих событию В.
![]() =
А – В.
=
А – В.
Определение 7.
Произведением
двух событий А
и В
называется событие, состоящее из исходов
принадлежащих и событию А
и событию В
одновременно, обозначается таким
образом:
![]() .
.
Пример 1. А –появление туза при вынимании карты из колоды, событие В – появление карты бубновой масти, то событие АВ – есть событие появление бубнового туза.
Пример 2. Пусть производятся два выстрела по мишени. А – попадение при первом выстреле, В – попадение при втором выстреле. То АВ – попадение при обоих выстрелах.
Определение 8.
Два события
А
и В
называются несовместными, если они не
имеют общих исходов, т.е.
![]() .
.
Введенные операции обладают следующими свойствами:
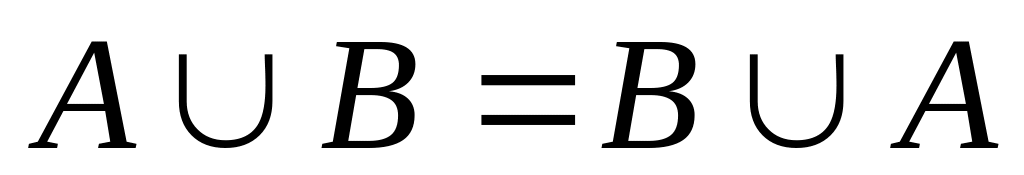 -
переместительный
закон,
-
переместительный
закон,
 -
-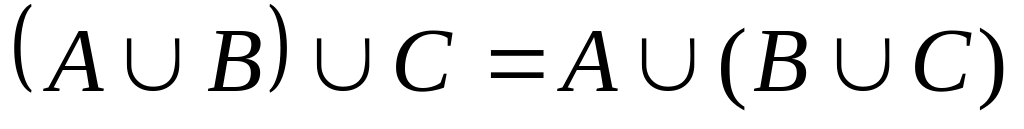
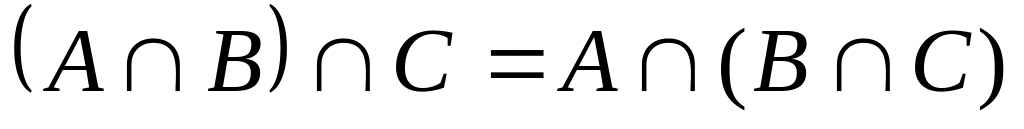



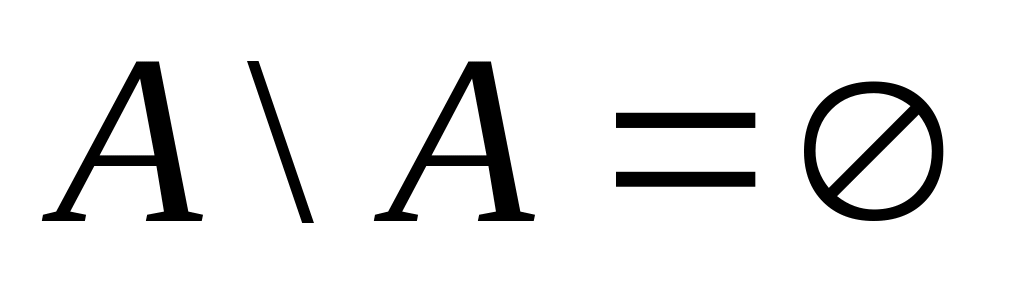
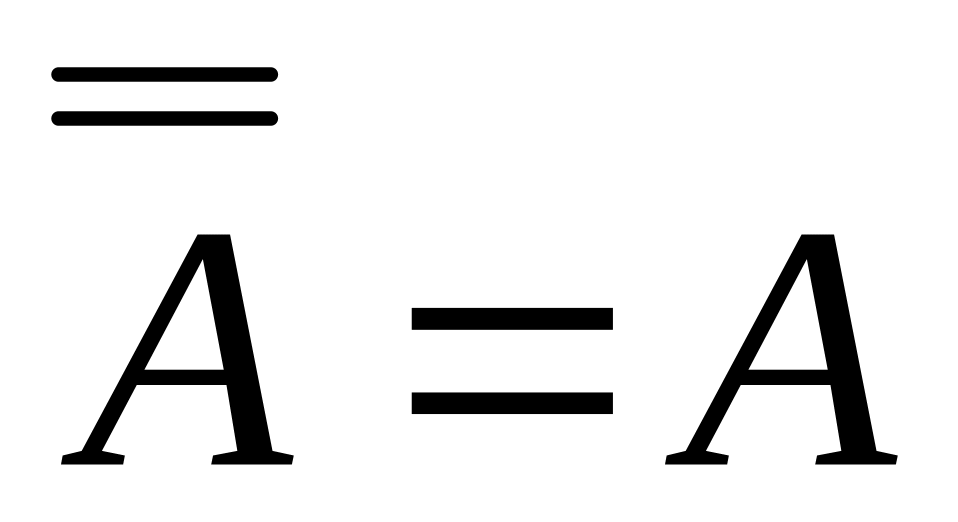

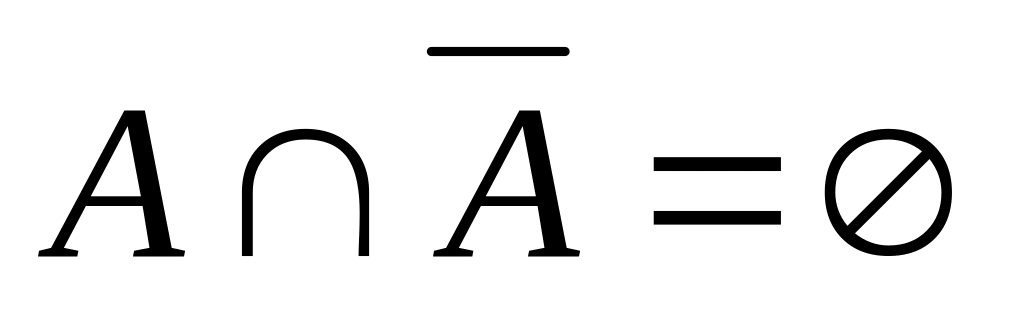
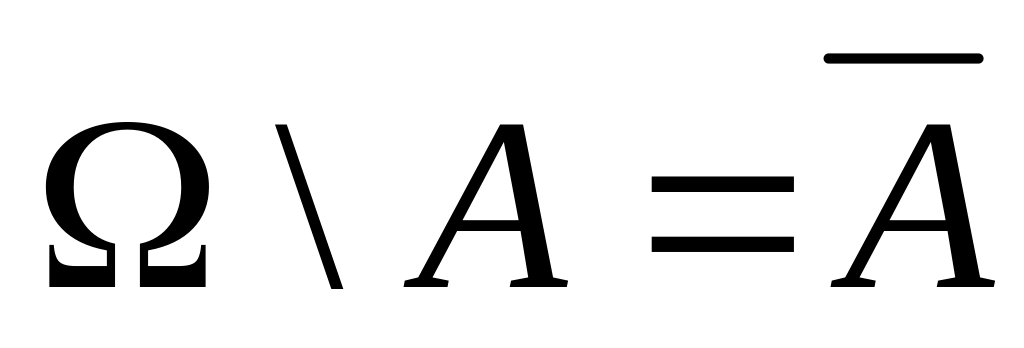




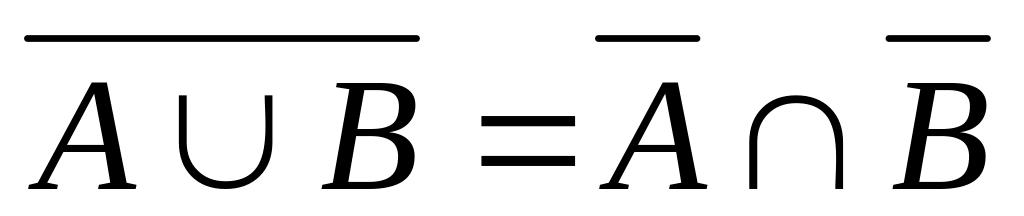

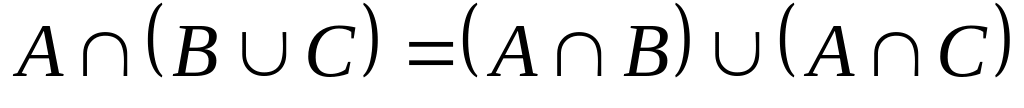
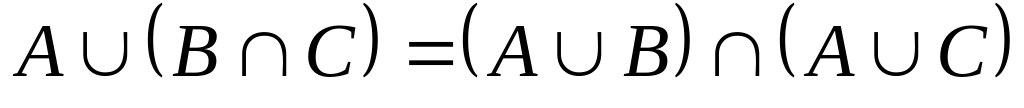
Система событий
![]() называется
полной группой событий, если она
осуществляет разбиение пространства
на попарно непересекающиеся события,
удовлетворяющие следующим условиям:
называется
полной группой событий, если она
осуществляет разбиение пространства
на попарно непересекающиеся события,
удовлетворяющие следующим условиям:
1)
![]() при
при
![]() ;
;
2)
![]() .
.
Пусть - пространство элементарных событий, соответствующее эксперименту с однократным подбрасыванием игральной кости. Тогда оно может быть разбито, например, на следующие полные группы событий:
1)
![]()
![]()
2)
![]()
![]()
![]()
