Министерство образования РТ
Альметьевский Государственный Нефтяной Институт
Кафедра АИТ
Курсовой проект
По курсу «Теория Автоматического Управления»
Выполнил студент гр. 52-61 Шарипов Л.М.
Руководитель курсового проекта:
Ахметова Р. Н.
Альметьевск 2005 г.
Содержание
Часть 1. Исследование линейной сар с пи-регулятором по
корневым критериям качества.------------------------------------------------------4
Определение
значений параметров настройки
и
для И, П
и ПИ-регуляторов.---------------------------------------------------------------------7
Определение переходных функций по задающему воздействию
для И, П и ПИ-регуляторов.--------------------------------------------------------10
Определение переходных функции по возмущающему воздействию
для И, П и ПИ-регуляторов.--------------------------------------------------------17
Определение АЧХ замкнутой САР-----------------------------------------------23
Определение АЧХ по ошибке------------------------------------------------------28
Вычисление интегральной квадратичной оценки-----------------------------32
Часть 2. Оценка качества переходных процессов сау по
интегральным квадратичным критериям.---------------------------------------39
Определение параметров для различных коэффициентов веса.------------41
Список использованной литературы---------------------------------------------44
Вариант 24
Часть 1
m1=0.33
m2=0.4
ky=2
T0=1.6
Часть 2
T1=1.0
T2=0.7
Часть 1 исследование линейной сар с пи-регулятором по корневым критериям качества
ЦЕЛЬ РАБОТЫ: исследование линейной системы автоматического регулирования с ПИ-регулятором по корневым критериям качества (степени колебательности).
Структурная схема исследуемой системы регулирования
x 
y
Передаточная функция разомкнутой системы
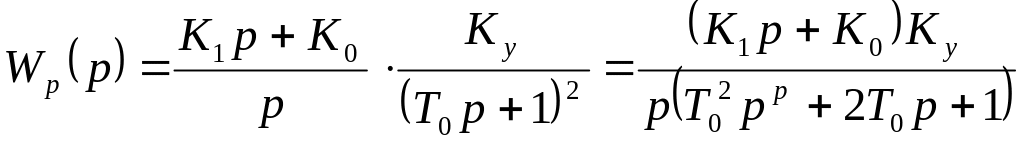
Характеристическое уравнение замкнутой системы имеет вид:
Сделав
замену
,
где
,
запишем смещенное уравнение
Для выполнения условия m = mзад необходимо, чтобы система находилась на границе устойчивости в новых координатах. Иными словами, смещенное уравнение должно иметь мнимые корни
Z = jλ
Построив границу Д-разбиения для смещенного уравнения в плоскости параметров К0 и К1 получим всю совокупность значений К0 и К1, при которых m = mзад. Граница Д-разбиения является линией равного m. В частном случае при m = 0 имеем границу области устойчивости. Для практических целей достаточно ограничиться положительными значениями К0 и К1. задаваясь различными значениями m, можно построить семейство линий равной колебательности, что позволяет производить выбор параметров регулятора.
Рассмотрим последовательность построения
линий заданного значения m.
Подставим в смещенное уравнение Z
= jλ и
,
получим уравнение границы Д-разбиения.
Раскрывая
скобки и приравнивая к нулю вещественную
и мнимую части уравнения получим систему
с двумя неизвестными:
Решая систему при различных значениях λ, найдем границу Д-разбиения. Решение удобно искать с помощью определителей:
К1 = Δ1/Δ; К2 = Δ2/Δ
где
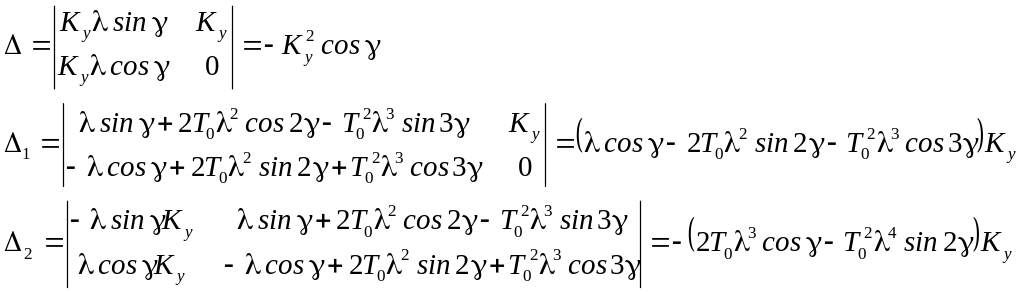
Подставив значения Δ, Δ1, Δ2 найдем К0 и К1 функции λ
Изменяя в пределах от нуля до бесконечности, построим кривую Д-разбиения. В частном случае для m = 0 найдем уравнение границы области устойчивости и построим эту область.
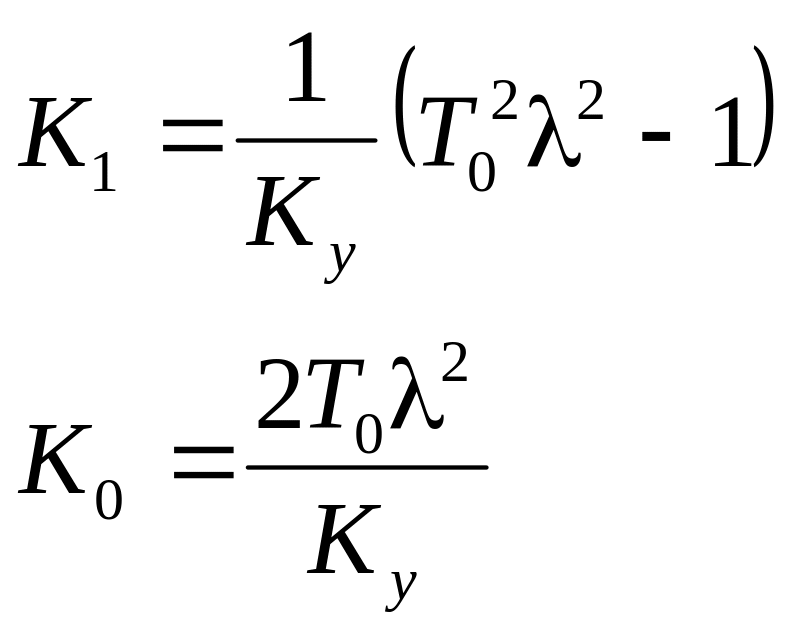
Кривая значения m = 0 для ПИ-регулятора
k0 = 1.6λ2
k1 = 1.28λ2 – 0.5
Кривые значений m1 = 0,33 для ПИ-регулятора
k0(λ) = 1.6 λ2 – 0.8 λ3
k1(λ) = 0.77 λ2 + λ – 0.5
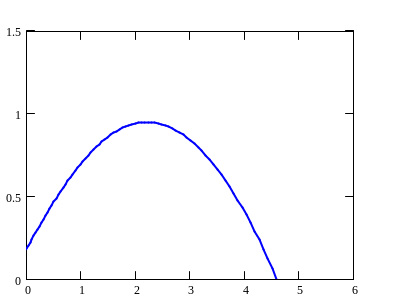
Кривые значений m2 = 0,4 для ПИ-регулятора
k0(λ) = 1.6 λ2 – 0.95 λ3
k1(λ) = 0.57 λ2 + 1.185λ – 0.5
