Порядок проведения лабораторной работы

Работа выполняется в диалоговом режиме.

Номер варианта, сообщаемый в ответ на запрос, задает некото­-рую конкретную функцию, минимум которой необходимо найти, и коли­чество допустимых испытаний.

Аналитическое представление этой функции студенту неизвестно. Задача студента заключается в том, чтобы для каждого из описанных выше методов:

а) последовательно указать точки вычисления функции (для ме­тода пассивного поиска точки должны быть упорядочены в порядке возрастания);

б) указать длину , и границы заключительного интервала неопре-деленности.

В помощь студенту на экран выводится следующая информация:

- для метода пассивного поиска: при неверно введенном значе-нии x_kвыводится сообщение об этом, после чего ввод должен быть повторен;

- для методов Фибоначчи и золотого сечения выводится график со значениями функций в уже выбранных точках; ниже графика выво-дятся сами точки в порядке указания; при неверном выборе очеред-ной точки выводится соответствующее сообщение, после чего ввод должен быть повторен.

- 7 -

Требования к отчету

Отчет должен содержать:

а) постановку решаемой задачи;

б) последовательность выбранных для испытаний точек и обосно­вание такого выбора;

в) длину и границы заключительного интервала неопределеннос­-ти;

г) ответы на контрольные вопросы.

Контрольные вопросы

1. В чем отличия в постановке задач, решаемых методами пас­сивного поиска, золотого сечения и методом Фибоначчи?

2. Как оценить скорость изменения интервала неопределенности в методах одномерной минимизации?

3. Чему равен выигрыш от использования метода золотого сечения по сравнению с методом пассивного поиска при n = 10?

Лабораторная работа 2

МНОГОМЕРНАЯ МИНИМИЗАЦИЯ

Цель работы. Исследование алгоритмов безусловной минимизации гладких функций нескольких переменных.

Постановка задачи

Для заданной функции ƒ(x¹,...,xⁿ)найти ее точку минимумаx_*с заданной точностью ε. Для поиска минимума воспользоваться различными методами минимизации, описываемыми ниже.

Краткие общие сведения. Градиентный метод с постоянным шагом

Общая схема метода следующая:

по заданному значению x₀ -вектору начального приближения -вычисляются последовательно значения x₁,x₂,... по формуле:

- 8 -

где - вектор частных произ- водных функции ƒ₁по координатамх¹, ..., x², вычисленный в точке.

Метод наискорейшего спуска

Отличие этого метода от градиентного метода с постоянным ша-гом заключается в способе вычисления параметра α_k наk-м шаге алгоритма:

x_k+1 = x_k – α_k ∙ grad ƒ(x_k),

α_k=argmin { ƒ( x_k – α ∙ grad ƒ(x_k)) : α > 0 }

Т.е. на каждом шаге используется дополнительная процедура одномер­ной минимизации (поиска точки локального минимума функции одного аргумента).

Метод Ньютона-Рафсона

Этот метод используется для вычисления точки локального мини­мума функции и переменных, обладающей третьими производными по всем переменным. Последовательность { x₁, x₂, ...} приближений к стационарной точке строится по формуле:

где

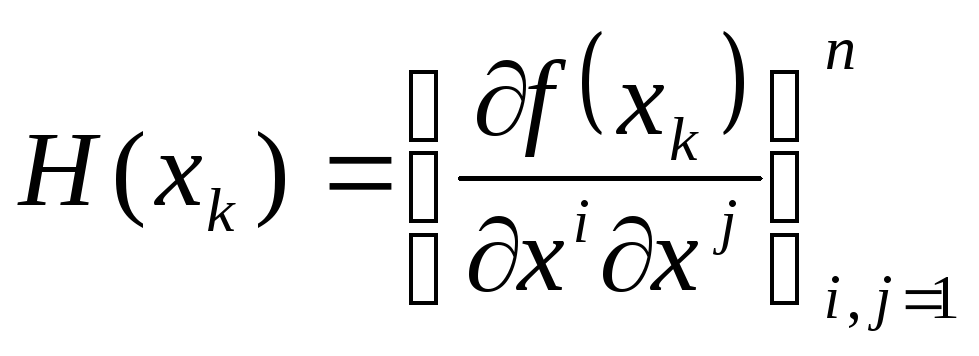- nxn- матрица Гессе

функции ƒ в точке x_k.

Порядок проведения лабораторной работы

Работа осуществляется в диалоговом режиме с помощью программы. Описанные выше методы исследуются на примере задачи минимизации квадратичной функции двух переменных ƒ(x) = ƒ(x¹,x²):

ƒ(x) = X^TAX + B^TX + C.

- 9 -

Параметры минимизируемой функции - 2х2 - матрица А, 2-векторВи скалярС -задаются студентом по указанию преподавателя.

В задачу студента входят:

а) определение начального вектора x₀и величины шага α, при котором значения ƒ(x1), ƒ(x2), ..., определенные градиентным методом с постоянным шагом, убывают;

б) проведение минимизации заданной функции методами наискорей­шего спуска и Ньютона-Рафсона;

в) сравнение результатов, полученных различными методами. В помощь студенту по окончании работы программы в соответствии с одним из методов на экран выводится таблица точек х_kи значенийƒ(x_k).