7

Санкт-Петербургский Государственный Электротехнический Университет «ЛЭТИ»

кафедра МО ЭВМ

Отчет

по лабораторной работе №5

Решение транспортной задачи

Выполнили: Воронин С.Ю.

Сергеев М.В.

Группа: 3352

Проверил: Балтрашевич В.Э.

Санкт-Петербург

2005г.

Лабораторная работа №5

РЕШЕНИЕ ТРАНСПОРТНОЙ ЗАДАЧИ

Цели работы:

Исследование метода потенциалов решения транспортной задачи.

Постановка задачи

Пусть заданы m пунктов снабжения, из которых продукт может транспортироваться в каждый из n пунктов потребления.

Производительность i-го источника равна α_i, а потребление j-го стока равно B_j; стоимость транспортировки единицы продукта из пункта i в пункт j равна С_ij.

Требуется найти такую схему транспортировки продукта, при которой общие транспортные затраты минимальны.

Предполагая, что выполнено условие баланса

(5.1)

выпишем математическую постановку задачи.

Минимизировать

(5.2)

при условии, что

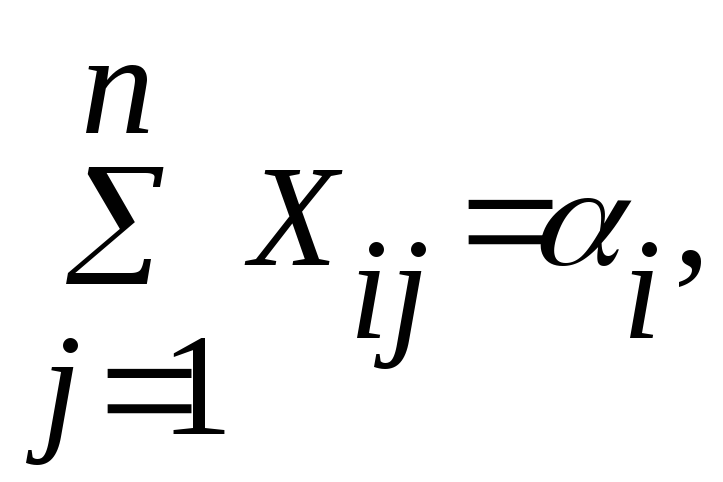i = 1, ..., m,

j = 1, ..., n,

X_ij ≥ 0, i = 1, ..., m, j = 1, ..., n.

Здесь X_ij - количество продукта, транспортируемого из i-го источника в j-й сток.

Исходные данные при решении задачи вручную удобно зафиксиро­вать в таблице вида табл. 5.1:

Таблица 5.1

αi	Bj	B1	...	Bn
α1		C11	...	C1n
...		...	...	...
αm		Cm1	...	Cmn

Краткие общие сведения

Общепринятым методом решения транспортной задачи является так называемый "метод потенциалов". Приведем структуру соответствующего алгоритма.

1. Поиск начального решения, т.е. набора {X_ij}, удовлетворяющего ограничениям (5.3).

2. Если {X_ij} - оптимальное решение, то конец.

3. Модификация решения, не увеличивающая его стоимости, и переход на 2.

Задача (5.2), (5.3) является частным случаем задачи линейного программирования, а вышеприведенный алгоритм укладывается в общую схему решения этой задачи.

Выделим специфические черты, отличающие метод потенциалов.

1. В силу (5.1) условие (5.3) содержит ровно m+n-1 независимых ограничений, и, следовательно, любое базисное решение транспортной задачи имеет не более m+n-1 ненулевых компонент.

2. Транспортная задача допускает несколько простых способов поиска начального базисного решения. Один из возможных алгоритмов реализован в лабораторной работе:

а) выбрать: в табл.5.1 незаполненную и непомеченную клетку с минимальной стоимостью (пусть, для определенности, это клетка с индексами (k, l));

б) заполнить выбранную клетку числом

X_kl = min { α_k, B_l },

т.е. максимально загрузить соответствующий путь;

в) модифицировать величины спроса и предложения:

1) α_k = α_k - X_kl

B_l = B_l – X_kl.

2) если α_k = 0,

то пометить все незаполненные и непомеченные клетки k-й строки,

иначе пометить все незаполненные и непомеченные клетки l -го столбца;

д) если остались незаполненные или непомеченные клетки,

идти на а).

Заполненные клетки будем называть базисными (некоторые из них могут содержать нули).

3. Проверку оптимальности полученного решения удобно осуществлять, переходя к двойственным переменным. Не входя в подробности обоснования, приведем соответствующий алгоритм:

а) найти "потенциалы" и, такие, что

U_i + V_j = C_ij (5.5)

для всех пар (i, j), выделяющих базисные клетки. Легко видеть, что одну из переменных U_i или V_j (по нашему выбору) можно положить равной чему угодно, после чего система (5.5) решается однозначно;

б) для всех небазисных клеток вычислить так называемые "характеристические разности"

X_ij = U_i + V_j - C_ij

в) если все X_ij отрицательны,

то решение оптимально,

иначе см. следующий пункт.

4. В случае если полученное решение не оптимально, можно относительно просто улучшить его:

а) выбрать какую-либо клетку, для которой X_ij < 0;

б) найти последовательность клеток (цикл)

(i₁=i, j₁=j), (i₂,j1), (i₂,j₂), ..., (i_p,j_p-1), (i_p,j_p), (i_p+1=i₁,j_p), в которой все клетки, кроме клеток (i₁,j₁), являются базисными;

в) перераспределить грузопоток по найденному циклу:

пропустить дополнительно X единиц груза по каждому из путей (i_k, j_k),

уменьшить на X количество груза, перевозимого по путям (i_k+1, j_k).

Здесь

(5.6)

г) включить в базис клетку (i, j) и исключить из базиса одну из клеток, поток в которой после модификации, проведенной в п. в), оказывается равным 0.

Вообще говоря, п. в) вышеприведенного алгоритма следует сводить к задаче поиска цикла в ориентированном графе (связанном с модифицируемым решением), однако при небольших размерах задач, решаемых в ходе лабораторной работы, цикл можно найти путем простого направленного перебора в глубину. Следует запомнить, что величина Х, вычисляемая в (5.6), может оказаться равной 0. При использовании такого цикла меняется не грузопоток, а лишь набор базисных переменных.