Лабораторная работа #1

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА МО ЭВМ

Дисциплина: Методы оптимизации

ОТЧЕТ

по лабораторной работе №1

«Исследование методов безусловной минимизации»

Выполнили студенты гр. 3352

Воронин С.Ю.

Сергеев М.В.

Проверил: Бaлтрашевич В.Э.

Санкт – Петербург

2005

1. Формулировка задания

Для функции f(x1, x2) = (x2 – x1²)² + a*(x1-1)² найти её точку минимума х^* с заданной точностью ε. Для поиска минимума воспользоваться следующими методами минимизации:

1. Градиентный с постоянным шагом

2. Градиентный с дроблением шага

3. Градиентный с убыванием шага как 1/k

4. Наискорейшего спуска

5. Метод Ньютона-Рафсона

6. Алгоритм Полака – Ривьера

7. Алгоритм Давидона – Флетчера – Пауэлла

8. Алгоритм Бройдена – Флетчера – Шано,

для следующих значений параметра a: 0.1; 1; 10

для следующих начальных точек: (3; 8); (2; 5); (4; 23)

2. Математическая постановка задачи

Градиентный метод с постоянным шагом

Общая схема метода следующая:

по заданному значению x₀ - вектору начального приближения– вычисляются последовательно значения x₁,x₂,... по формуле:

где - вектор частных производных функции ƒ₁ по координатам х¹, ..., x², вычисленный в точке .

Метод наискорейшего спуска

Отличие этого метода от градиентного метода с постоянным шагом заключается в способе вычисления параметра α_k на k -м шаге алгоритма:

x_k+1 = x_k – α_k ∙ grad ƒ(x_k),

α_k = argmin { ƒ( x_k – α ∙ grad ƒ(x_k)) : α > 0 }

Т.е. на каждом шаге используется дополнительная процедура одномер­ной минимизации (поиска точки локального минимума функции одного аргумента).

Метод Ньютона

Если f(x) является дважды дифференци­руемой в Rⁿ, то эффективность процесса поиска точки х* ее минимума можно повысить, используя информацию не толь­ко о градиенте этой функции, но и о ее матрице Гecce H(x). Алгоритмы такого поиска обычно относят к ме­тоду Ньютона. В простейшем варианте алгоритма на каждой k-й итерации целевая функция аппроксимируется в окрестно­сти точки xk-1 (на первой итерации в окрестности начальной точки х0) квадратичной функцией и затем определяется точка xk минимума функции . На следующей, (k+1)-й итерации строится новая квадратичная аппроксимация уже в окрестности точки xk.

Начальный этап:

Выбрать x0, , k=1.

Основной этап

Шаг 1

(1) Строится Ньютоновское направление:- градиент в заданной точке, H – матрица Гессе

(2) Найти как результат решения системы уравнений

(3)

(4)

Шаг 3

Проверить КОП: если , то , иначе на Шаг 1.

Метод Ньютона-Рафсона

Этот метод используется для вычисления точки локального мини­мума функции и переменных, обладающей третьими производными по всем переменным. Последовательность { x₁, x₂, ...} приближений к стационарной точке строится по формуле:

где

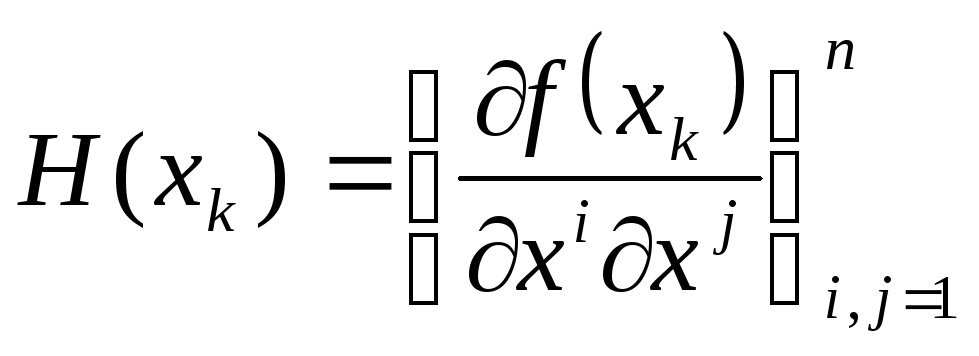- n x n - матрица Гессе функции ƒ в точке x_k.

Квазиньютоновские методы

Особенность этих алгоритмов состоит в том, что при их применении нет необходимости вычислять и обращать матрицу Гессе целевой функции f(x) и в то же время удается сохранить высокую скорость сходимости алгоритмов, присущую методу Ньютона и его модификациям

Элементы релаксационной последовательности {x^k} в ал­горитмах квазиньютоновских методов минимизации непрерыв­но дифференцируемой в Rⁿ целевой функции f(x) строят в соответствии с рекуррентным соотношением , но направление спуска на каждой k-й итерации задают в виде .

Начальный этап

Выбрать x¹, , k=1.

Основной этап

Шаг 1

(1) Строится корректирующая матрица:

(2)

(3)

Шаг 3

Проверить КОП: если , то , иначе на Шаг 1.

Формула метода Давидона-Флетчера-Пауэлла

, где

Формула метода Бройдена-Флетчера-Шенно

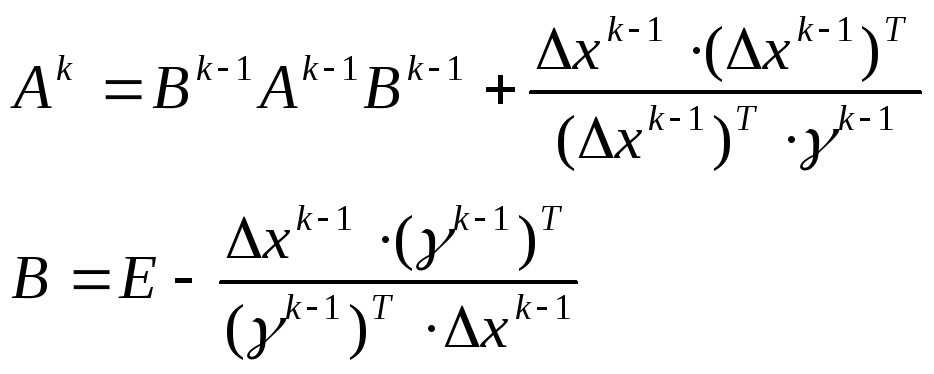
Метод сопряжённых направлений

Метод сопряжённых направлений основан на свойствах векторов сопряженных относительно некоторой квадратной матрицы. Различие в способах построения системы сопряженных векторов, определяющих сопряжённые направления спуска, порождает несколько алгоритмов этого метода. В качестве матрицы сопряжений берётся матрица Гессе. Особенность алгоритмов метода сопряженных направле­ний состоит в том, что систему сопряженных векторов строят последовательно в процессе выполнения итераций, причем найденный на очередной, k-й итерации вектор pk определяет на этой итерации направление спуска. Для не квадратичных функций получаемые направления, в конце концов, перестают быть взаимносопряженными поэтому, как и в ДФП через n шагов вектор направления делают равным антиградиенту.

Начальный этап

Выбрать x¹, , k=1.

Основной этап

Шаг 1.

Построить вектор pk:

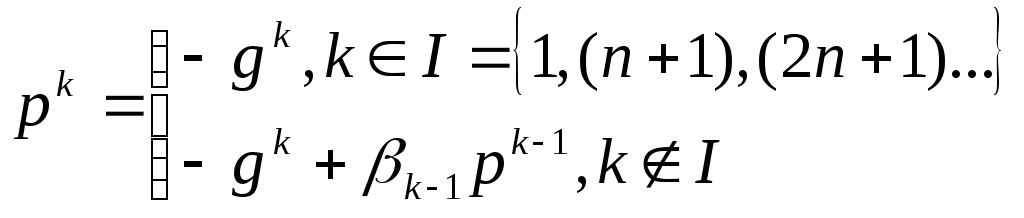
Шаг 2.

Найти новую точку как результат одномерного поиска полученного направления .

Шаг 3.

Проверить КОП: .

Расчетное соотношение Полака-Рибьера

3. Испытания методов оптимизации

Метод	Количество шагов k
	x0 = (3, 8)			x0 = (2, 5)			x0 = (4, 23)
	a = 0.1	a = 1	a = 10	a = 0.1	a = 1	a = 10	a = 0.1	a = 1	a = 10
1. Градиентный с постоянным шагом	15000	1600	350	12500	1300	200	*	5500	800
2. Градиентный с дроблением шага	15000	1600	350	12500	1300	200	*	5500	800
3. Градиентный с убыванием шага как 1/k	*1	*	*	*	*	*	*	*	*
4. Наискорейшего спуска	200	30	15	180	10	11	500	73	25
5. Метод Ньютона-Рафсона	30	10	4	25	9	3	180	10	80
6. Алгоритм Полака-Ривьера	12	7	4	7	5	3	13	8	5
7. Алгоритм Давидона-Флетчера-Пауэлла	15	9	3	9	5	3	20	9	3
8. Алгоритм Бройдена-Флетчера-Шанно	15	9	3	11	5	3	24	11	4

4. Сравнительный анализ методов оптимизации

Градиентные методы (кроме метода с убыванием шага как 1/k) дают глобальную сходимость (т.е. мало чувствительны к исходным данным). Градиентный метод с убыванием шага как 1/k показал очень медленную скорость сходимости, что не позволило определить минимум функции ни в одной их исходных точек. Этот метод очень сильно чувствителен к выбору начальной точки (исходная точка должна быть близка к х^*). В целом, градиентные методы показали медленную сходимость.

Метод Ньютона и его модификации оказались быстрее градиентных методов (обеспечивается квадратичная сходимость). Особая чувствительность к исходным данным не выявлена.

Квазиньютоновские методы показали очень высокую скорость сходимости и малую чувствительность к исходным данным.

Следует отметить, что ньютоновские и квазиньютоновские методы накладывают жесткие ограничения на исходную функцию (должна быть несколько раз дифференцируема в данной точке), а также требуют большого объема вычислений, в ряде случаев, связанных с вычислением матрицы вторых производных и её обращения.

Хотя градиентные методы обладают слабой скоростью сходимости, они относительно просты в вычислении.

Вывод: Были исследованы методы безусловной оптимизации, проведен их сравнительный анализ.

1 * - не удалось найти минимум (число шагов более 27000)

5