Краткие общие сведения Метод Пассивного поиска
Этот метод предназначен для локализации точки минимума функ-ции ƒ при "одновременном" вычислении значений ƒ в nточках: вы- бор этих точек не зависит от вычисляемых, быть может, последовательно, значений функций ƒ в этих точках.
Пусть n≥ 2,x1, x2, ...,xn- точки вычисления функции ƒ, О≤x1≤x2≤...≤xn≤1. Тогда, очевидно
Ln=max{x2, x3-x1, ..., xn-xn-2,1-xn-1}.
1. n- четно. Тогда оптимального выбора последовательностиx1,...,xnне существует, но для любого ε >0существует ε - оптимальная последовательность:
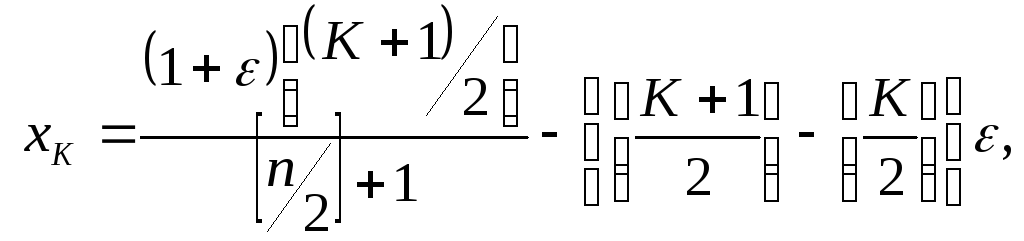
где [α] - целая часть α.
- 4 -
При этом величина интервала неопределенности равна
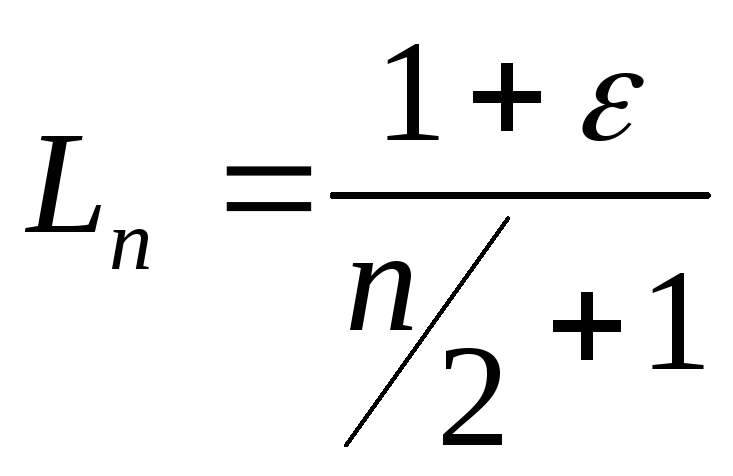
Последовательность x1,...,x2состоит изn/2 ε-пар, точек, рас-стояние между которыми равно ε:
и
т.д.
Если ƒ(xk)≥ ƒ(xk+1) и ƒ(xk+1)≤ƒ(xk+2), то ясно, что в интервале [xk,xk+2] функцияƒимеет локальный минимум.
Если ƒ(x1)≤ ƒ(x2), минимум лежит в интервале[0, x2];если ƒ(xn-1) ≥ ƒ(xn), - то в интервале[xn-2, 1). Длина каж- дого из этих интервалов равнаLn.
Отметим, что величина ε определяется погрешностью вычисления функции ƒ.
2. n– нечетно. Тогда оптимальных способов выбора последова-тельностиx1,...,xnбесконечно много. Например, такой:
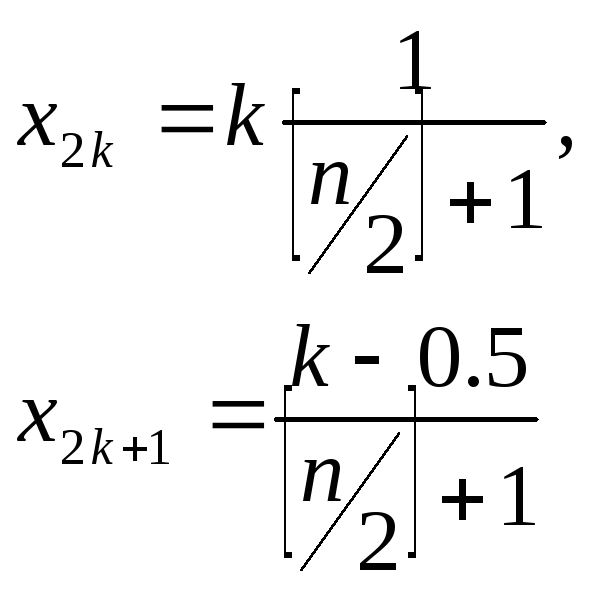
При
этом
.
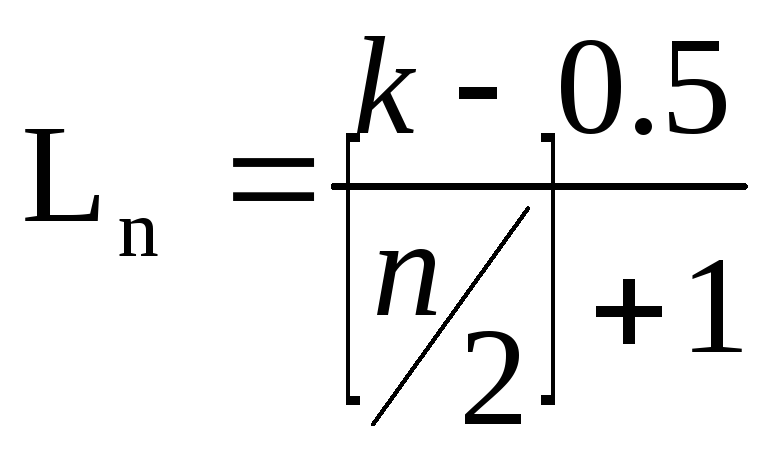Отметим, что уменьшение числа точек вычисления функции ƒ на одну приведет (при использовании указанной в п.1 последовательности) к увеличению Lnвсего наε/([n/2]+1).
Метод Фибоначчи
Этот метод применяется, если известно точное количество испытаний n, и при выборе значенияxkк-го испытания можно использовать информацию о значениях ƒ(x1),..., ƒ(xk-1)(k>=2). После каждого испытания интервал неопределенности сокращается. При этом используется следующий факт: если α<Bи ƒ(α)>=ƒ(c), ƒ(B)>=ƒ(c), то на интервале[α,B]находится точка локально- го минимума непрерывной функции ƒ.
- 5 -
Здесь потребуются числа Фибоначчи, удовлетворяющие равенствам:
F1=F2=1,
Fn+2=Fn+Fn+1.
Нетрудно
убедиться, что
.
Определим α1=0,B1=1, x1=Fn-1/Fn+1,x2=Fn/Fn+1.
Если ƒ(x1)≥ƒ(x2), то положим α2=x1,B2=B1;
Если ƒ(x1)<ƒ(x2), то положим α2=α1,B2=X2.
Для n ≥ k ≥ 2:
Yk+1 =αk+Fn-k/Fn+1,
Zk+1= αk+Fn-k+1/Fn+1.
В одной из этих точек значение ƒ на K-м шаге уже вычислено. Другую точку обозначимxk+1. Если ƒ(Yk+1)≤ƒ(Zk+1), то по- ложим αk+1=αk,Bk+1=Zk+1; если ƒ(Yk+1)>ƒ(Zk+1), то положим αk+1=Yk+1, Bk+1=Bk. Точка локального минимума лежит в интервале[αk, Bk]при всехk≥1, при этомBk+1-αk+1=Fn-k+2/Fn+1. Последняя точка xnвыбирается равнойYn+ε илиZn-ε, в за- висимости от того, в какой из этих точек вычислено значение ƒ. Здесь0<ε<1/Fn+1. Тогда длина заключительного интервала неопределенности равна1/Fn+1+ε.Можно доказать, что для лю- бого алгоритма заnиспытаний получить заключительный интервал неопределенности для любой (наихудшей для этого алгоритма) функции ƒ, меньший, чем 1/Fn+1,невозможно.
Метод золотого сечения
Нетрудно заметить, что в методе Фибоначчи
Отметим, что
при n→ ∞
- 6 -
Поэтому при больших n
|
|
(1.2) |
Выбирая значения xkтак же, как и в методе Фибоначчи, за исключением замены формулы (1.1) на (1.2), получаем почти такую же последовательность точек{x1,...,xn} стой разницей, что в (1.2) правая часть не зависит отn. Полученный метод называется методом золотого сечения (эти сечения указаны в (1.2)) и применяется в том случае, если числоnзаранее неизвестно. Отметим, что
и
при больших заданных nметод золотого
сечения хуже метода
Фибоначчи, в
= 1.1708...раз.