4.4. 1 Определение доверительных интервалов

Пусть количественный признак X генеральной совокупности распределен нормально. Найден доверительный интервал, покрывающий параметр μ с надежностью γ. Будем рассматривать выборочную среднюю как случайную величину и выборочные значения признака х₁ х₂,…, x_n - как одинаково распределенные независимые случайные величины Х₁ Х₂,..., Х_n имеющиеся от выборки к выборке. Математическое ожидание каждой из этих величин равно μ и среднее квадратичное отклонение - σ.

Примем без доказательства, что если случайная величина

распределена нормально, то выборочная средняя Х найденная по независимым наблюдениям, также распределена нормально. В соответствии с [ ] математическое ожидание среднего арифметического одинаково распределённых взаимно независимых случайных величин равно математическому ожиданию μ каждой из величин, а среднее квадратичное отклонение среднего арифметического п этих величин в раз меньше среднего квадратического отклонения а каждой из величин, то есть

M(X) = μ, σ(Х) = σ/

Потребуем, чтобы выполнялось соотношение

Р(|Х-μ |<σ)=γ (4.37)

где γ - заданная надёжность.

3.4.3 Оценка достоверности гипотез распределения

Для выполнения расчетов надёжности необходимо располагать достоверными сведениями о законах распределения анализируемых величин. Обычно имеющиеся данные такого рода не являются полными и достаточными. Более того, сведения о распределении наблюдаемых исследуемых случайных величин (характеристиках нагрузок, прочности, отказов и т.д.) также могут содержать элементы случайности,

Начальные суждения о распределении получают на основе статистических данных о случайных величинах (например, отказах). Эти данные корректируют с учетом поправок на систематическую погрешность и определяют среднее арифметическое уточненных результатов контрольных наблюдений. Далее оценивают их среднее квадратичное отклонение и проводят “сглаживание” статистических данных, отбрасывая резкие отклонения и сохраняя наиболее типичные свойства явления.

Согласование статистических зависимостей представляет собой задачу с неопределённостью, так как ее решение будет зависеть от выбираемых и налагаемых условий, которые полагаются наилучшими. Например, можно получить эмпирическую зависимость для распределения на основе применения метода наименьших квадратов, то есть выбрать функцию, сумма квадратов отклонений которой от статистических значений будет минимальной.

Можно основываться на соображениях о физической природе рассматриваемых явлений. Если принимается нормальное распределение, то очевидно необходимо, чтобы математическое ожидание m_х и дисперсия теоретического нормального

Распределения D_х соответствовали аналогичным характеристикам m_х и D_x полученного статистического распределения. Для получения лучших соответствий целесообразно вычислять моменты более высоких порядков (метод Пирсона), но пользоваться моментами выше четвертого .порядка нецелесообразно из-за резкого падения точности вычисления моментов по мере увеличения их порядков. Считается вполне достаточным совпадение первых трех моментов.

После выбора закона распределения необходимо проверить его представительность. Пусть полученное статистическое распределение удалось выразить теоретической кривой f(x), имеющей отклонения от статистической зависимости. В этом случае важно оценить характер расхождений, которые могут быть обусловлены случайными факторами, ограниченным числом наблюдений или несоответствием выбранного теоретического распределения "действительному". Для оценки соответствия используются критерий согласия, который наиболее часто используют в виде, предложенном АН. Колмогоровым. Метод основан на определении модуля разности между статистической F*(x) и теоретической F(x) зависимостями распределения (рис. 4.11)

Δ = max[F*(x) - F(x)]. (4.30)

Рис. 4.11. Сравнение функций F* (х) и F(x) и модуль разности между функциями.

А.Н. Колмогоров доказал, что при любой функции распределения F(x) непрерывной случайной величины n, и при неограниченном возраставши числа X независимых наблюдений вероятность неравенства

(4.31)

характеризуется пределом

. (4.32)

Значения функции Р(λ) могут быть найдены из таблицы [ ].

Применяют критерий Колмогорова следующим образом: сравнивают статистическую функцию распределения F*(x) с предполагаемой теоретической функцией F(x) и определяют максимум Δ модуля разности между ними (рис.4. 11). Далее определяют величину и по таблице находят

вероятность Р(λ) . При малой вероятности гипотезу распределения отвергают как неправдоподобную, и наоборот. Очевидно, что критерий Колмогорова можно применять лишь в случаях, когда известен вид функции F(x) и входящие в неё числовые параметры.

В качестве критериев согласия для проверки правильности принятой гипотезы распределения используют и другие критерии, в частности - критерий Пирсона, именуемый также критерием х² [ ].

На практике, из-за сложности и дороговизны постановки эксперимента, мы обычно располагаем статистическими данными ограниченного объема. Этих данных оказывается недостаточно, чтобы найти неизвестный закон распределения случайной величины. Однако, имеющиеся данные могут быть обработаны и использованы для получения некоторых сведений о случайной величине для оценки важнейших параметров закона распределения. При нормальном законе распределения это будут математическое ожидание μ и дисперсия σ² случайной величины. Значения искомых параметров, вычисленное на основе ограниченного ряда опытов, являются приближенными и – называются оценкой параметров.

Для математического ожидания оценкой может служить среднее арифметическое наблюдавшихся значений случайной величины

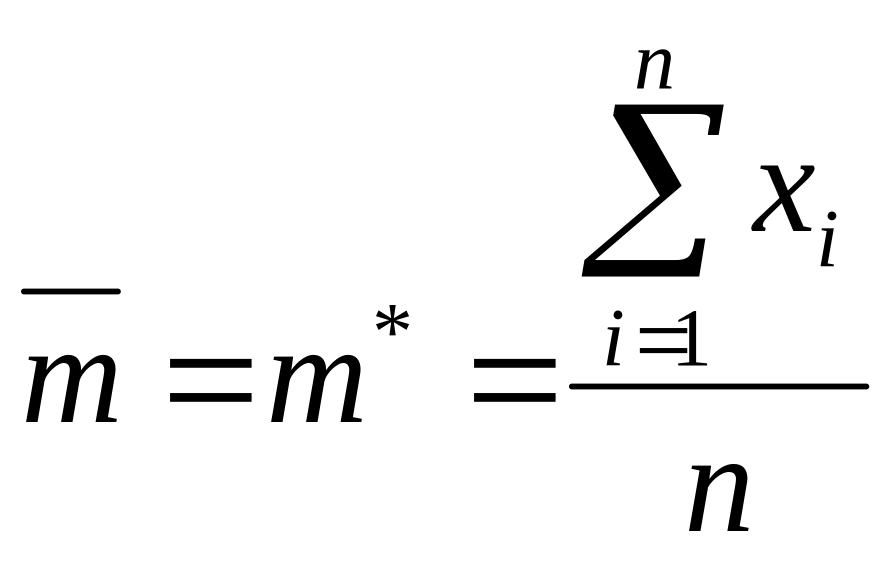(4.33)

где х₁ х₂, ..., х_n - наблюдавшиеся значения; n - число независимых опытов.

Чем меньше n, тем больше ошибка такой оценке, следовательно, оценка будет также случайной величиной, закон

распределения которой зависит от распределения величины X и от числа опытов п.

Ранее отмечено, что оценка параметра должна удовлетворять требованиям состоятельности_, эффективности и несмещенности. Среднее арифметическое ( 4.31) первым двум требованиям удовлетворяет, поскольку М[ ]=m, дисперсия этой оценки равна D[m]=D/n и при данном объеме выборки минимальна. В качестве наиболее естественной оценки можно было бы использовать статистическую дисперсию, определяемую по формуле

(4.34)

Но при этом не выполняется требование несмещенности поскольку математическое ожидание M(D* ) не равно D

(4.35)

Для устранения смещенности необходимо умножить значение статической дисперсии D* на коэффициент и в качестве исправленной статической дисперсии использовать оценку дисперсии

(4.36)

Оценка D для дисперсии при малом числе опытов не является достаточно корректной.

Оценка точности и надежности оценок параметров может быть точечной и интервальной. Точечная определяется одним значением, а интервальная - двумя, соответствующими концам принимаемого интервала. Отметим, что при небольших объемах выборки целесообразнее интервальная оценка.

Рассмотрим более подробно интервальные оценки. Положим, что найденная по данным выборки статистическая характеристика θ^* служит оценкой неизвестного параметра θ, соответствующего какому-то определенному числу θ^* тем точнее определяет параметр θ, чем меньше абсолютная величина разности |θ-θ*|. При некотором малом положительном числе δ требуется обеспечить |θ-θ*|<δ. Чем меньше δ, тем оценка точнее. Таким образом, положительное число δ характеризует точность оценки.

Однако, статистические методы не позволяют категорически утверждать, что оценка θ^* удовлетворяет неравенству |θ-θ*|<δ . Можно говорить лишь о вероятности γ, с которой это неравенство осуществляется. Здесь, γ=Р[|θ-θ*|<δ], последнее можно заменить равносильным двойным неравенством

Р[|θ*- δ < θ < θ*+δ в *]=γ (4.38)

согласно которому γ представляет собой вероятность того, что интервал (θ*-δ, θ*+δ) заключает в себе параметр θ.

Доверительным называют интервал θ*-δ, θ*+δ , который покрывает неизвестный параметр с заданной надежностью γ. Для примера определим доверительный интервал для оценки математического ожидания μ нормального распределения при известном среднем квадратическом отклонении σ .