3.4.3.3. Логарифмически нормальное распределение
Стандартный вид формулы для плотности случайной величины у>0 имеет вид
.
(4.22)
Параметры μ и σ2 выражают соответственно математическое ожидание и дисперсию случайной величины Inу (!), распределенной по нормальному закону. Наработка на отказ у многих невосстанавливаемых изделий может быть оценена логарифмицески нормальным распределением.
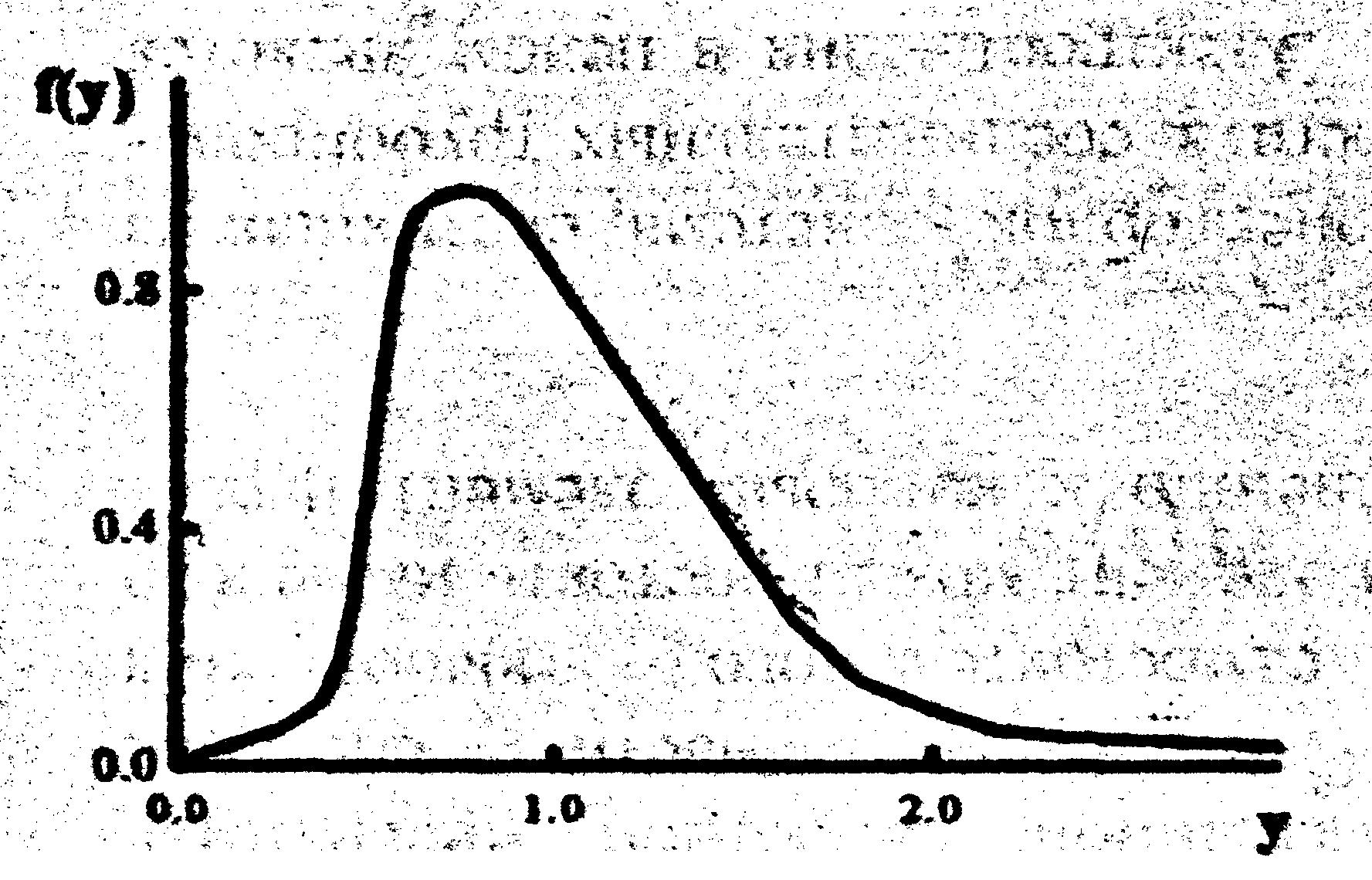
Рис. 4.8 Плотность логарифмически нормального распределения вероятностей.
ЗЦ3.4. Распределение Вейбулла
Распределение Вейбулла- частные случай экспоненциального закона распределения, и его часто используют для оценки наработки до отказа некоторых невосстанавливаемых изделий, у которых отказ наступает вследствие усталостного разрушения. Функция распределения Вейбулла может быть представлена в виде
,
(4.23)
где
а,
b,
τ0
-
положительные
константы
(параметры распределения),
причем
.
При
получим двухпараметрическое
распределение
и
зависимость для безотказной
работы в виде.
(4.24)
Зависимость (4.24) табулирована. Плотность вероятности определяется по выражению
.
(4.25)
Квантиль tp найдется по уравнению
.
(4.26)
Величины отношений t/a и tр/a для уравнений (4.25) и (4.26) могут быть представлены в таблицах. Кривая плотности распределения Вейбулла иллюстрируется на рис.4.9.
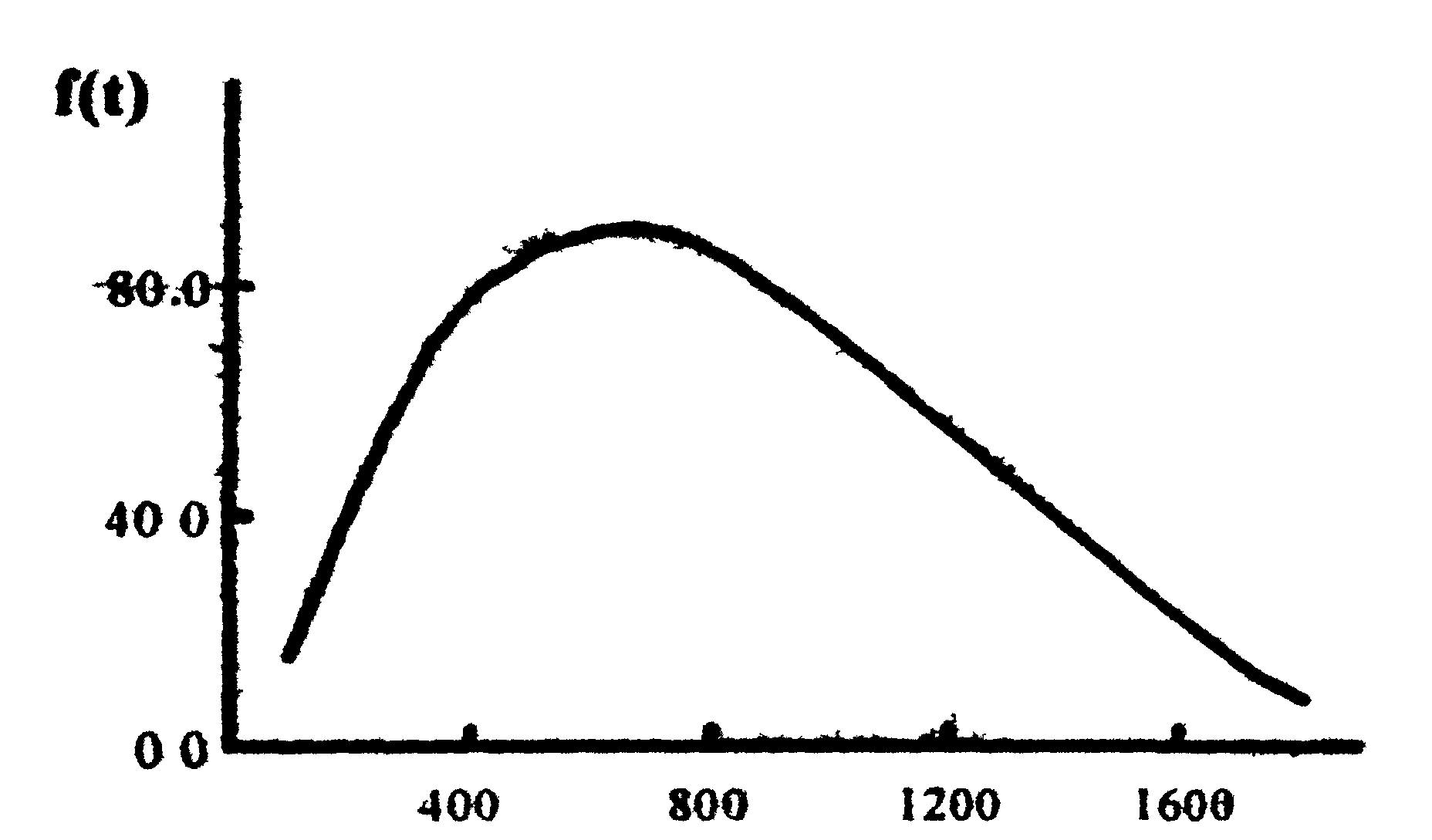
Рис.4.9. График плотности распределения Вейбулла.
Ранее рассматривались одномерные случайные величины. Однако, реальные процессы зависят от многих случайных величин (факторов), поэтому описание вероятности такого процесса представляется случайной величиной, которая зависит от многих, в частном случае, нескольких случайных величин. Наиболее часто используются двумерные случайные величины значения, которых определяются двумя числами. В этом случае закон распределения двумерной случайной величины можно представить в виде соотношения возможных значений пары чисел и их вероятностей. Удобно задать распределение таких величин в виде таблицы (см. рис. 4.10).
|
x1 |
x2 |
… |
xn |
y1 |
|
|
|
|
y2 |
|
|
|
|
… |
|
|
|
|
ym |
|
|
|
|
Рис. 4.10. Вероятности случайной
двумерной величины.
В первой строке такой таблицы указываются все значения составляющей X, а в первом столбце - возможные значения составляющей Y. В клетках на пересечении столбца хi и строки yj указывается вероятность существования случайной величины хiyj. По аналогии с одномерной величиной применяется характеристика плотности вероятности для непрерывной двумерной случайной величины и соответствующая ей функция распределения.
Для характеристики плотности распределения используется условное математическое ожидание двумерной случайной величины, которое называется функцией регрессии Y на X (или X на Y). Следует отметить, что в этом случае случайные величины могут быть как независимыми, так и зависимыми. Для численной характеристики системы двух случайных величин используется корреляционный момент μху и коэффициент корреляции Rху, определяемый отношением корреляционного момента к произведению средних квадратичных отклонений двух рассматриваемых величин
.
(4.27)
Наложение характеристик вероятности двумерных случайных величин можно найти в[ ].