2.3 Элементы теории вероятностей в анализе надёжности турбоустановок

Чтобы количественно сравнивать между собой события (например, отказы оборудования турбоустановок) по степени их вероятности, необходимо с каждым из событий связать характерное число, которое тем больше, чем вероятнее событие.

2.3.1 События

В качестве иллюстрации событий воспользуемся классическим примером случайных событий, которые в теории вероятностей связываются с исходами многократно повторяемых экспериментов. Для таких экспериментов мысленно используем два игральных кубика. Каждое испытание (бросание кубика) приводит к некоторому случайному исходу (случайному элементарному событию). Например, для двух кубиков можно получить множество сочетаний

1,1; 1,2; ...; 3,4; 4,4;...; 5,6; 6.6, (3.1)

если не делать различия между симметричными исходами 1,2 и 2,1,3,4 и 4,3, и т.д.

Но можно случайное событие определить. Налагая некоторое условие, например, считая его происшедшим, если сумма выброшенных очков будет равна 7. В этом случае требования выполняются при следующих исходах

1,6; 2,5; 3,4. (3.2)

При каждом испытании это событие происходит или не происходит. Следовательно, для данного выбора-события характерно свойство вероятности.

Применительно к турбоустановке каждому сочетанию событий можно считать соответствующим какой-либо вид отказов - поломок (поломка рабочих лопаток, выход из строя масляного насоса и т.д.).

Условие можно изменять и, полагая событием равенство числа очков на обоих кубиках, имеем следующие дискретные случайные события

1,1; 2,2; ... ; 6,6. (3.3)

Изложенное позволяет сделать следующие выводы. Множество всех возможных исходов (3.1) будем называть пространством элементарных событий Ω, то есть

£2=(1,1; 1,2 ..........; 5,6; 6,6), (3.4)

а событием - некоторое подмножество пространства Ω, которое удовлетворяет принятому критерию или требованию. Таким образом, имеем события

А₁= (1,6; 2,5; 3,4), (3.5)

А_{2=(1,1; 1,2; ...; 6,6).} (3.6)

Поскольку понятие событий связано с понятием множеств, рассмотрим некоторые основные их особенности.

3.2 Множества

Как выше установлено, события обладают свойством вероятности и представляются в виде множеств. Под множеством понимается некоторый набор элементов, в общем случае неупорядоченных и не образующих последовательности. Если х₁, х₂, ..., х_n - элементы множества А, то это множество можно записать в виде

А={х₁, х₂, ..., х_n}. Σ (3.7)

Если х принадлежит множеству А, то это обозначается х А.

Множество называется конечным, если оно состоит из конечного числа элементов, и бесконечным в противном случае. Множество, не содержащее ни одного элемента называется пустым (обозначение Ø). Множество Ω называется основным, если оно содержит все рассматриваемые элементы. Если каждый элемент множества А₁ входит в множество А₂, то А₁ называют подмножеством А₂ и обозначают А₁ А_2.

Очевидно, что пустое множество Ø служит подмножеством любого множества (Ø А и Ø В). Если А₁ А₂ A₃, то и А₁ А₃. Если А₁ А₂, а А₂ А₁, то А₁=А2.

Логической суммой (дизъюнкцией) или объединением A₁U А₂ двух множеств А₁ и А₂ называется множество, которое содержит все элементы, принадлежащие хотя бы одному из множеств A₁ и А₂, т.е. x (A₁ U А₂) означает x A₁ или х А_2, или х А₁ и х А₂, Это понятие иллюстрируется графически диаграммой Венна (рис. 3.1, а).

(рис. 3.1, а).

Аналогично определяется объединение любого числа множеств: если А_i - произвольное множество, то U_iA_i - совокупность элементов, принадлежащих хотя бы одному из множеств А_i.

Логическим произведением (конъюнкцией) или пересечением

A₁ А₂ двух множеств A₁ и А₂ называют множество, которое содержит все элементы, входящие и в A₁, и в А₂ одновременно, т.е. x (A₁ A₂) означает х A₁ и же A₂ (рис.3.1,б).

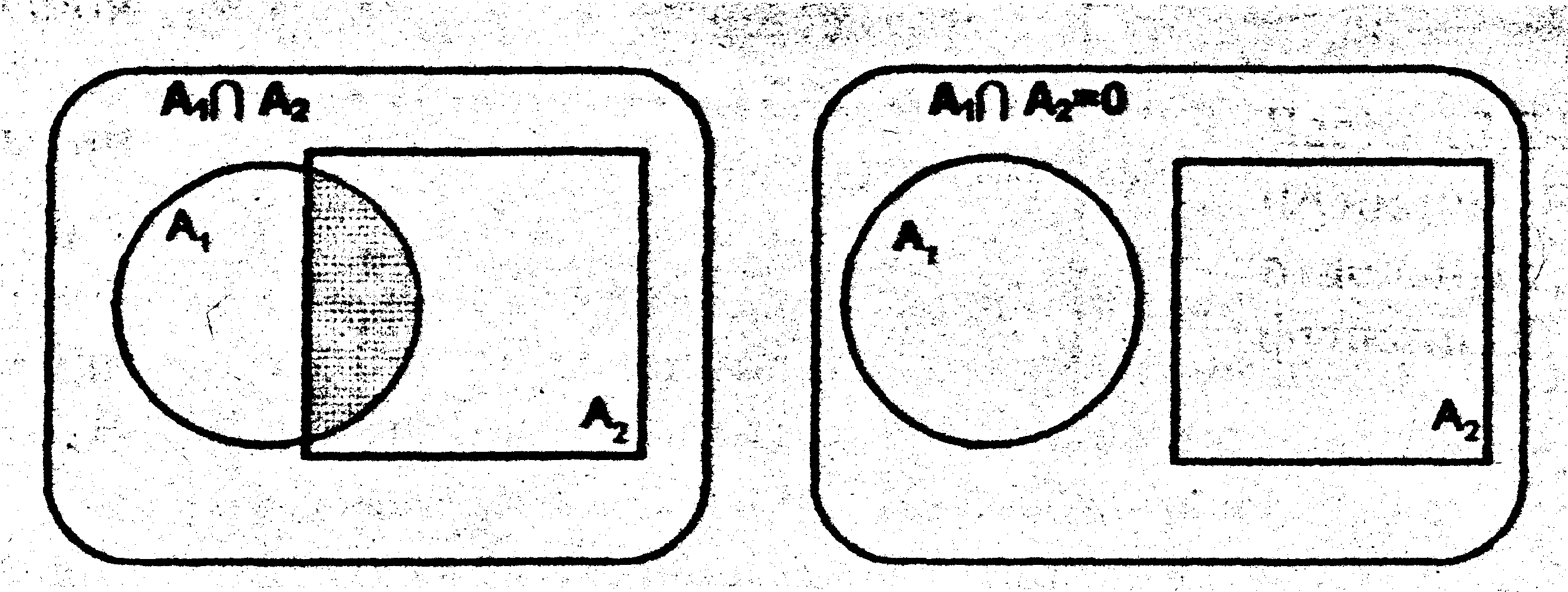
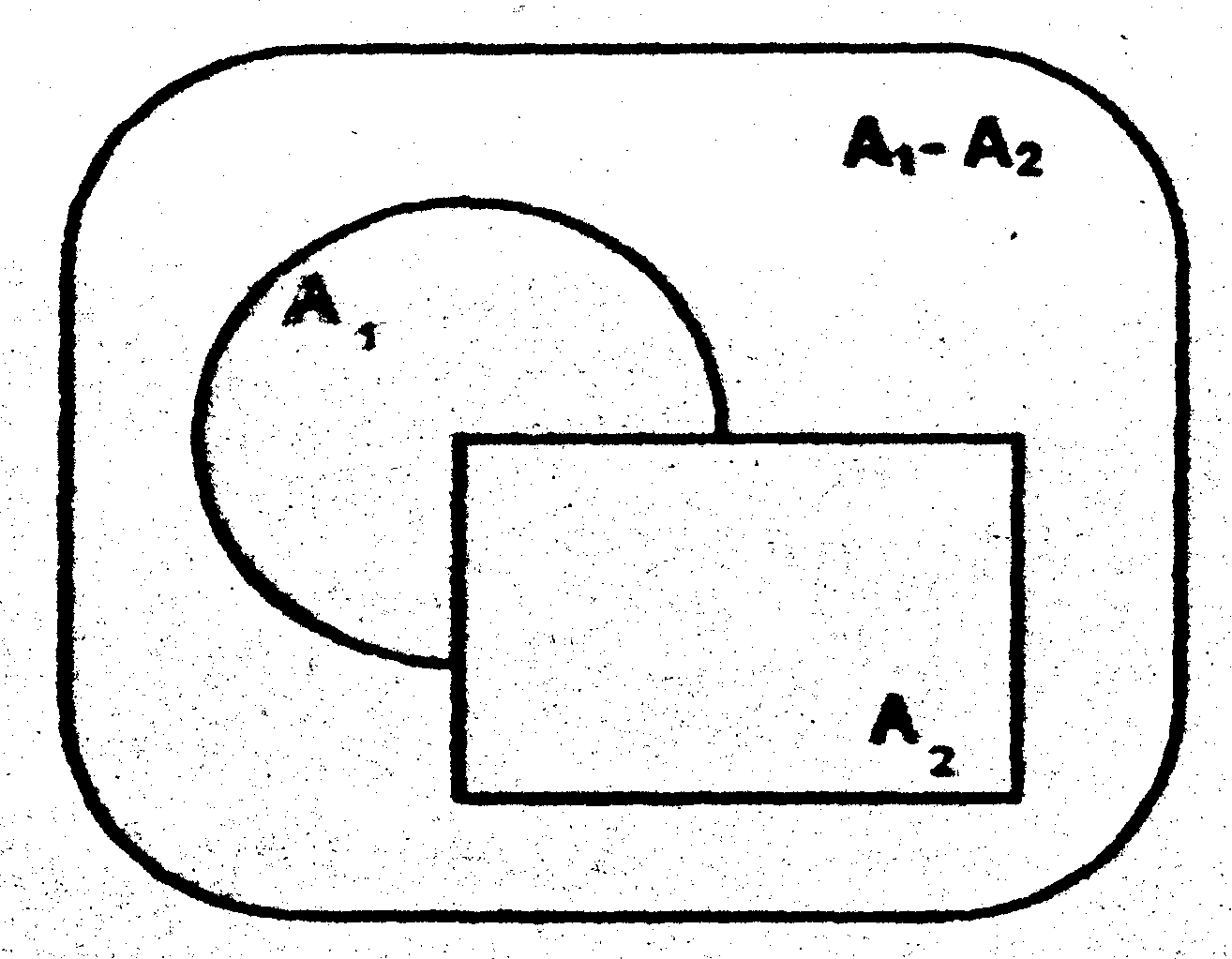
Разностью А₁ - А₂ множеств A₁ и А₂ называется совокупность тех элементов А₁ которые не содержатся в А₂, т.е. x (A1 - А₂) означает х А и х А₂ (рис. 3.1, в).

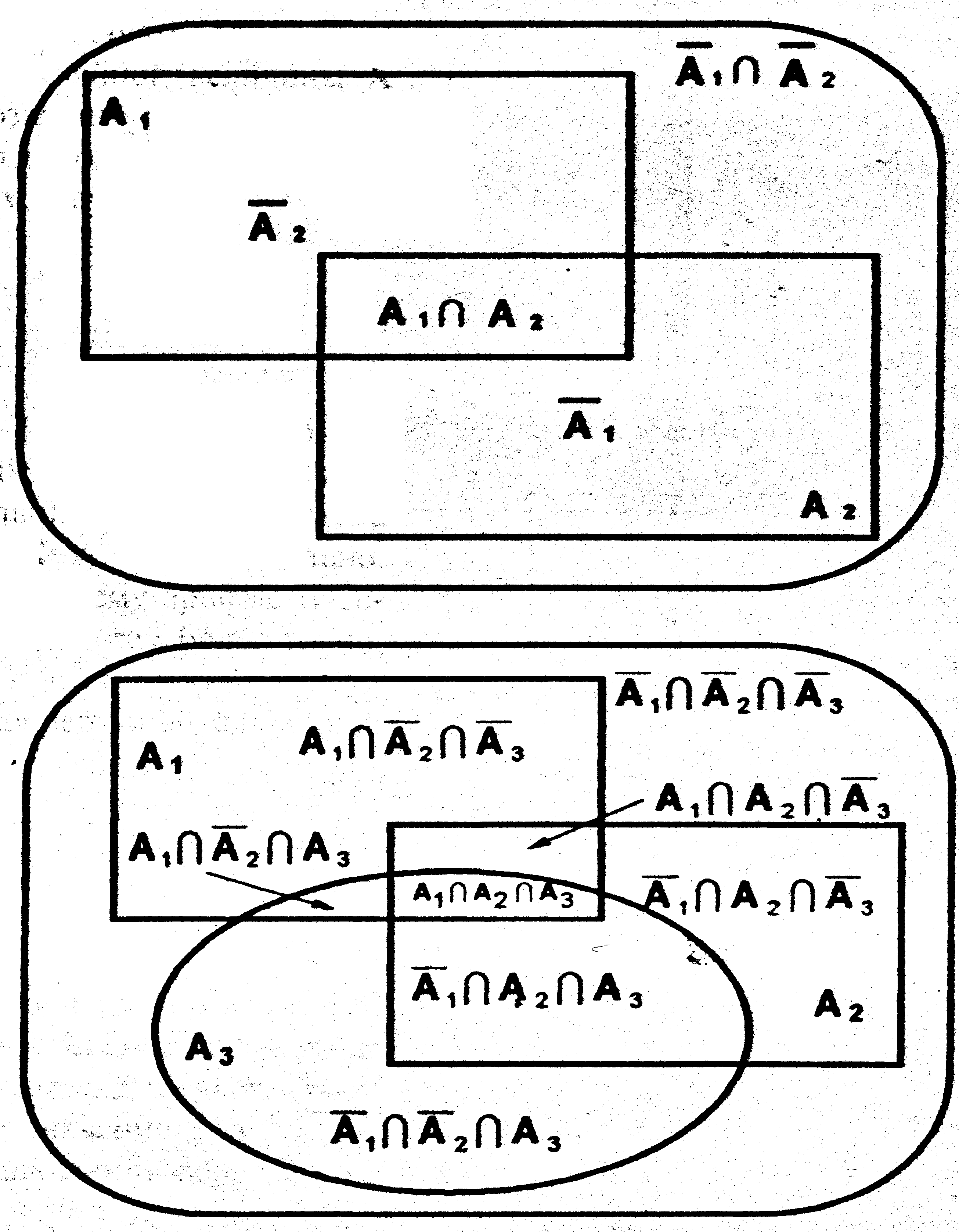
p(A₁ A₂)=p(A₁)+p(A₂).

Несколько событий в опытах называются равновозможными, если из условий симметрии ни одно из этих событий не является объективно более возможным. Например, отказ в работе любой турбоустановки из группы однотипных, находящихся в одинаковых условиях эксплуатации, равновозможен.

Если группы событий обладают указанными ранее тремя свойствами, то есть образуют полную группу, несовместны и равновозможны, то их называют случаями. Случай полагается благоприятным для события, если его появлению соответствует появление данного события.

Утверждения (3.8)-(3.10) называются аксиомами вероятности, которые позволяют определить правила оперирования с вероятностями. Но только с их помощью нельзя найти вероятности конкретных событии. Численные значения вероятностей возможно определить на основе опытов или логических рассуждений. Существует два типа подходов, один из которых основан на использовании экспериментальных данных {апостериорные вероятности), а другой - на предварительных суждениях (априорные вероятности). В соответствии с первым подходом для решения практических задач находятся действительные распределения вероятности событий, например, отказов.

Пример 3.1: На ТЭС имеется пять однотипных установок, находящихся в одинаковых условиях эксплуатации. Турбоустановки имеют номера с 1 по 5. Пусть выходу из строя турбоустановок с четными номерами 2 и 4 соответствуют два благоприятных случая (событие А), а отказу турбоустановок с нечетными номерами (1, 3, 5) - три благоприятных случая (событие В).

Вероятность события А в рассматриваемых вариантах событий можно априорно оценить по относительной частоте благоприятных случаев

ω(А)=т/п, (3.11)

где ω(А) - относительная частота появления события А, m -абсолютная частота случаев, благоприятных событию А; о -общее число случаев. Пример 3.2: На ГПС устанвлены семь газоперекачивающих агрегатов: №1, ..., №7, отказы которых равновозможны. Вероятность того, что выйдет из строя агрегат с номером не меньше 5, равна отношению числа возможных «благоприятных» отказов (3) к общему числу возможных отказов, т.е. 3/7. Отметим, что этот результат мы снова получили на основе рассуждений, без экспериментов.

Априорный подход основывается на понятии равновозможных исходов. Полагая, что все исходы равновозможны, определяем вероятность события отношением числа возможных «благоприятных» исходов мысленного эксперимента к числу всех возможных исходов.

Формула (3.11) применялась в начальный период развития теории надежности в качестве оценки вероятности события. В настоящее время пользуются иным принципом определения вероятности - понятием эмпирической (относительной) частоты или статистической вероятности события.

Пример 3.3. Производится серия п стендовых циклических испытаний на - усталостную прочность турбинных лопаток, имеющих одинаковые геометрические размеры, изготовленных из стали одной марки (20X13) и при одинаковых условиях нагружения (амплитуда изгибиого напряжения, число циклов нагружения). Событием А будем считать соответствие числа опытов с появлением трещин на поверхности лопаток. Частотой

события А для данной серии испытании полагаем отношение числа отказов т, в которых появилось событие А, к общему числу испытаний п

Р(А) =т/п. (3.12)

При малом числе опытов в определение частоты событий отношением т/п имеет случайный характер и является приближенным. По мере роста п значение Р(А) уточняется и точное значение Р(А) имеет вид

(3.13)

Определение вероятностей комплексных событий обычно вызывает трудности н часто невозможно, поэтому используют косвенные методы определения вероятности одних событий через известные вероятности других событий, связанных с первыми. Такие методы базируются на основных теоремах теории вероятностей.

При анализе надёжности многоэлементного оборудования турбоустановок используют понятия суммарной, условной и полной вероятности.

2.3.4 Суммарная вероятность

Суммой двух событий А и В называют событие С, состоящее в выполнении события А \или события В или обоих событий вместе. Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.

Пример 3.4: Отказ ГТУ может быть обусловлен выходом из строя

турбины, генератора или обоих элементов ГТУ вместе. Пусть

событие А - отказ турбины, В - отказ генератора и С - отказ

энергетической ГТУ.

Для решения задачи воспользуемся одной из важнейших теорем о суммировании вероятностей: вероятность суммы двух несовместных событий равна сумме вероятностей частных событий, или

Р(С) = Р(А+В)=Р(А) + Р(В) (3 14)

Пример 3.5: ГТУ имеет две симметрично расположенные выносные камеры сгорания. Выход из строя любой из камер приводит к отказу ГТУ. Вероятность отказа ГТУ по причине выхода из строя первой камеры сгорания обозначим P(A₁), а второй - Р(А₂). Таким образом, вероятность отказа ГТУ по причине выхода из строя камер сгорания выражается как

P(A₁+A₂) = Р(А₁) + P(A₂).

Эта теорема имеет следствие, которое гласит: вероятность появления одного из нескольких несовместных событий, безразлично какого, равна сумме вероятностей этих событий

P(A₁+A₂+...+A_п) = Р(А₁) + Р(А₂) + ... + P(A_п). (3.15)