(4.6)

где в каждое произведение А входит m раз, а входит n-m раз.

Вероятность каждой последовательности событий, отображаемых формулой (4.6), по теореме умножения вероятностей для независимых событий, равна р^m q^n-m. Так как общее число таких последовательностей равно _nС_m, то, используя теорему сложения вероятностей для несовместных событий, получим вероятность события В_m, (обозначим ее Р_m,n).

Р_n,m=_nC_m^. p^{m .} q^n-m

или (4.7)

Полученную формулу называют формулой Бернулли, а повторяющиеся испытания, удовлетворяющие условию независимости и постоянства вероятности появления в каждом из них события А, называют испытаниями Бернулли или схемой Бернулли.

Поскольку события В_т при т = 0,1,2,.....п несовместны и отражая различные числа появлений события А в п испытаниях, образуют полную группу, имеем

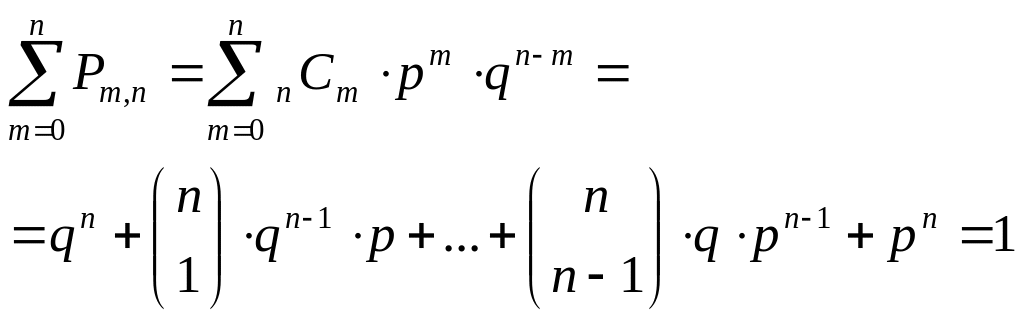(4.8)

Видим, что правая часть равенства (4.9) представляет собой составляющие разложения бинома

(4.9)

Пример 4.1: На газоперекачивающей станции (ГПС) установлено десять газоперекачивающих агрегатов (ГПА). Какова вероятность выхода из строя каких-либо двух установок, если вероятность отказа любой из установок равна 5%?

Пример 4.2: При условиях примера определить вероятность ситуации, когда не работают не более двух ГПА.

Математическое ожидание и дисперсия биномиального распределения определяются по следующим формулам

μ=n ^.p и σ²=n ^.p ^.q

Распределение Пуассона: Формулу Пуассона получим на основе предельного перехода для биномиального распределения. При этом полагается, что и np - остаётся конечным при . Обозначая m=np, согласно (4,5) имеем

(4.7)

При сделанных предположениях

, и при n>>r имеем

(4.8)

Подставив полученные значения в (4.7) имеем распределение Пуассона

Постоянная m есть параметр распределения, причем существует условие

(4.9)

Для распределения Пуассона математическое ожидание и дисперсия определяются по следующим формулам

σ²=m и μ=m.

4.2. Понятие об интенсивности отказов

Рассмотрим в качестве случайной величины X количество отказов в течение интервала времени 0-t. Чтобы найти функцию распределения X, разобьем интервал 0-t на п меньших интервалов, длительностью Δt и предположим; что Δt выбрано настолько малым, что на протяжении одного такого периода может произойти всего один отказ_. Предположим также, что среднее число отказов в единицу времени λ постоянно. Это означает, что среднее число отказов в течение интервала 0-t равно MX=np(x=1;t), и поэтому, p(x=1;Δt)=λt/n=λ Δt .

3.2 Непрерывные распределения

Для качественной характеристики распределения непрерывной случайной величины обычно используют не вероятность события Х= х, а вероятность события Х<х, где х - некоторая текущая переменная. Вероятность такого события является функцией от х и обозначается F(x). При этом функция F(x)=P(X<x) называется функцией распределения случайной величины или интегральной функцией распределения.

Первая производная функции распределения называется плотностью распределения вероятности непрерывной случайной величины

f(x) = F'(x). (4.10)

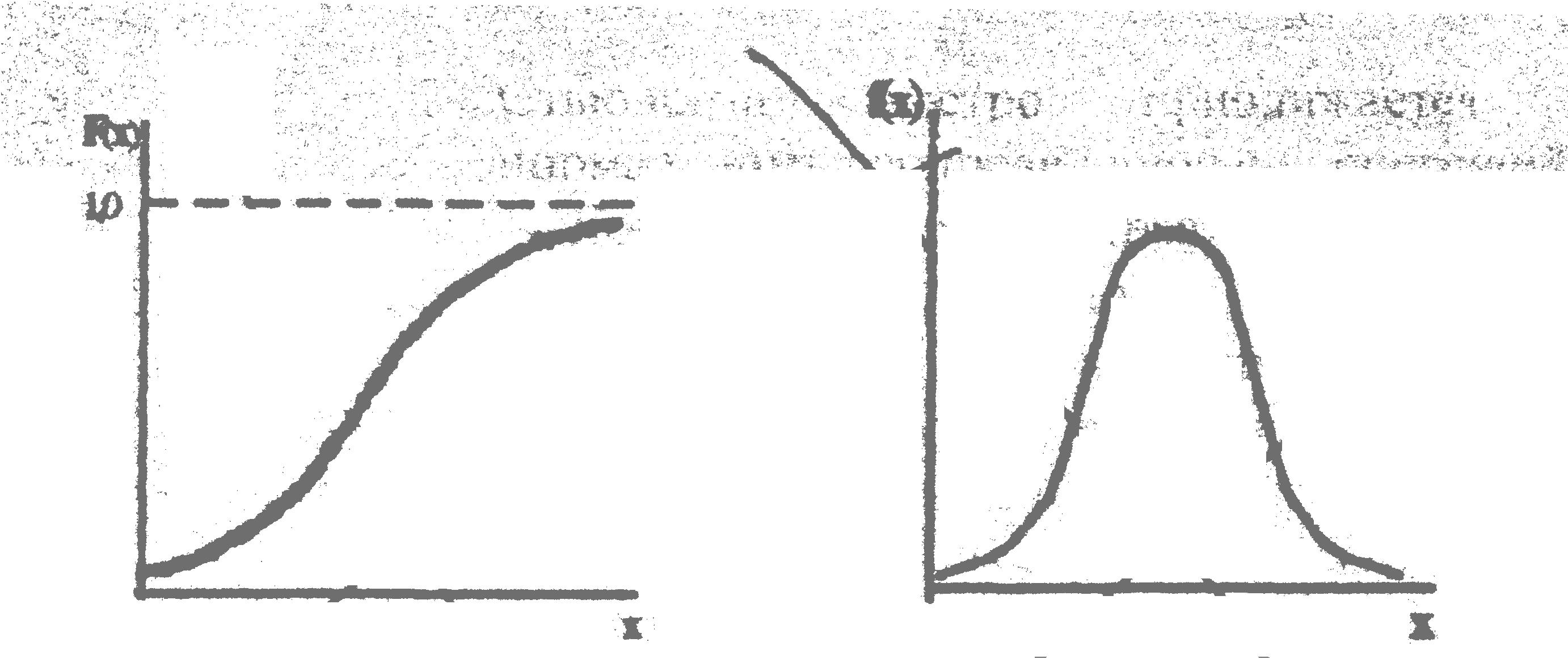
Обычно функция распределения непрерывна. Плотность распределения также непрерывна и всегда положительна (см. рис.4.2 и рис.4.3).

Рис.4.2 Общий вид функции распределения непрерывной случайной величины	Рис. 4.3 Кривая плотности распределения непрерывной случайной величины

3.4.1 Экспоненциальное распределение

Экспоненциальное распределение может быть использовано для оценки наработки на отказ многих восстанавливаемых изделий. Функция этого однопараметрического распределения

F(τ)=1-e^-λτ, (4.11)

где τ- наработка по времени (τ>0), λ - параметр распределения. Вероятность безотказной работе до наработки t равна

P(τ)=e^-μτ, (4.12)

Плотность вероятности экспоненциального распределения

φ(τ)=λ ^. exp(-λτ), (4.13)

Экспоненциальное распределение применимо при анализе внезапных отказов в случаях, когда явления износа и старения слабо выражены. Экспоненциальное распределение может также представлять наработку между соседними отказами в период приработки для восстанавливаемых изделий, В первом приближении время восстановления изделий также может быть представлено экспоненциальным законом. Для наработки, заданный уровень вероятности определяется квантилью τ_р

Р = ехp(-τ_р). (4.14)

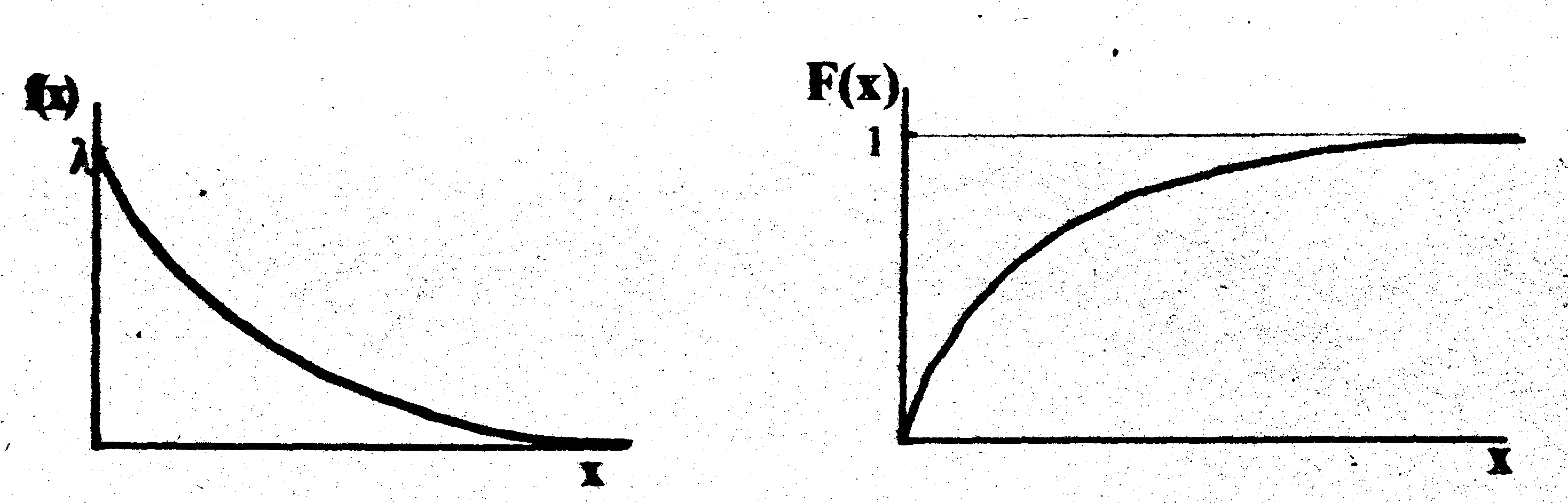
Рис.4.4 Плотность вероятности экспотенциального распределения	Рис. 4.5 Распределение вероятности по экспотенциальному закону

4.3.2. Нормальное распределение

Наиболее часто используется при описании различных процессов вероятностного характера, например для представления ошибок измерений. В некоторых случаях нормальный закон используется для оценок наработки на отказ невосстанавливаемых изделий.

Главная особенность нормального закона в том, что он служит как бы предельным законом, к которому приближаются другие законы распределения вероятности.

Функция нормального распределения

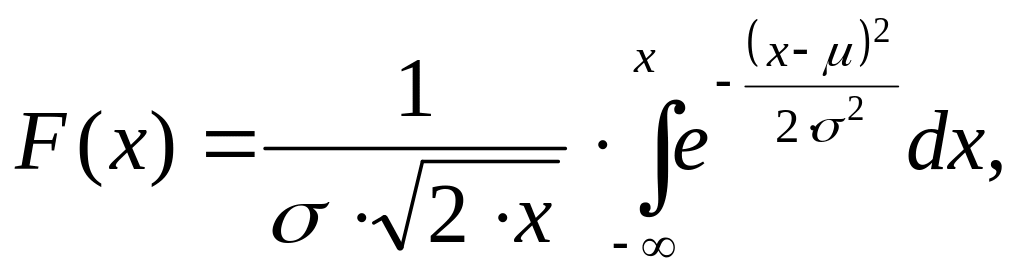(4.15)

где μ- математическое ожидание и σ² - дисперсия (σ - среднеквадратичное отклонение). Следовательно нормальное распределение задается двумя параметрами.

Из(4.15)следует, что F(- )=0 и F( )=1.

Плотность распределения

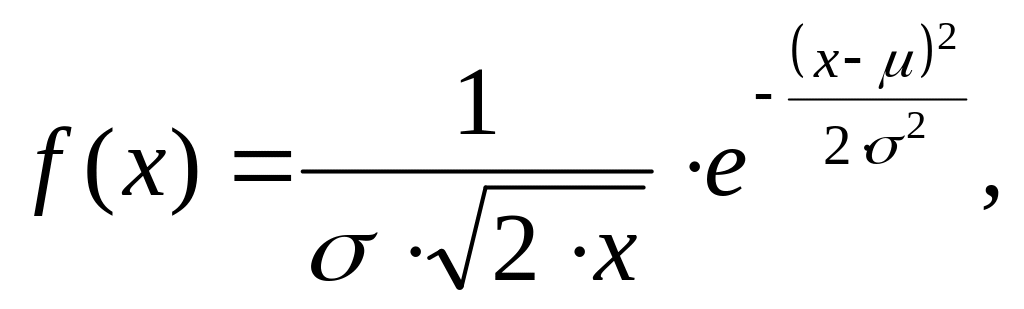(4.16)

Для удобства вычисления функций распределения используют нормированные (σ =1) и центрированные (μ=0) функции распределения

(4.17)

Очевидно, что F₀(- ) = 0, F₀( ) = 1 и F_o(-x) = 1- F₀(х).

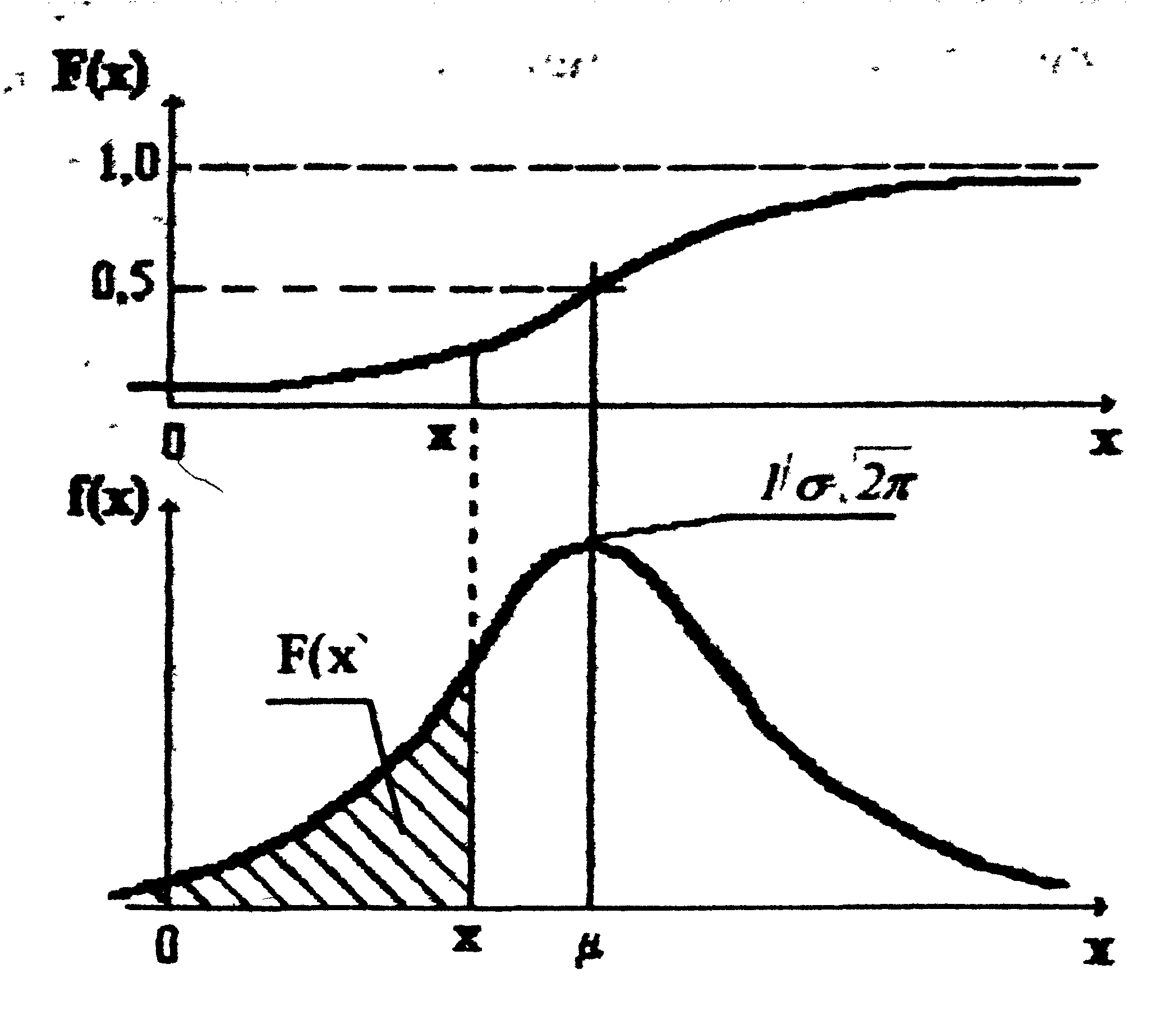
Рис. 4.6. Функция распределения вероятности и плотность функции нормального распределения непрерывной случайной величины.

Функция (4.17) затабулирована.

На основе сопоставления формул для F(x) и F₀(x) получим равенство

(4.18)

которое и позволяет легко пользоваться для вычисления F(x) указанными выше таблицами для F₀(x).

Аналогично можно получить нормированную и центрированную плотность распределения f₀(x) и использовать соотношение

. (4.19)

Так как нормальное распределение широко применяется при решении задач надёжности, то рассмотрим его особенности подробнее.

Отметим, что неопределенный интеграл вида (4.15) нельзя выразить через элементарные функции. Определенный интеграл может быть вычислен с заданной точностью численными методами.

Для вычисления функции распределения вероятности при нормальном распределении может быть использована (и используется) нормированная функция Лапласа, которая представлена определенным интегралом вида

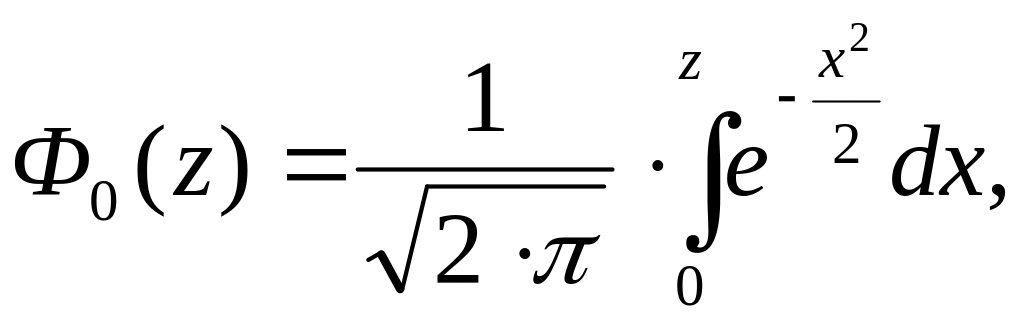(4.20)

выражающим площадь под кривой f(х)=ехр(-х²/2) в диапазоне от 0 до z (рис. 4.7).

Значения нормированной функции Лапласа даны в соответствующих таблицах.

Из (4.20) следует, что , и , а также .

Нормированную и центрированную функцию нормального распределения (4.17) можно представить как

(4.21)

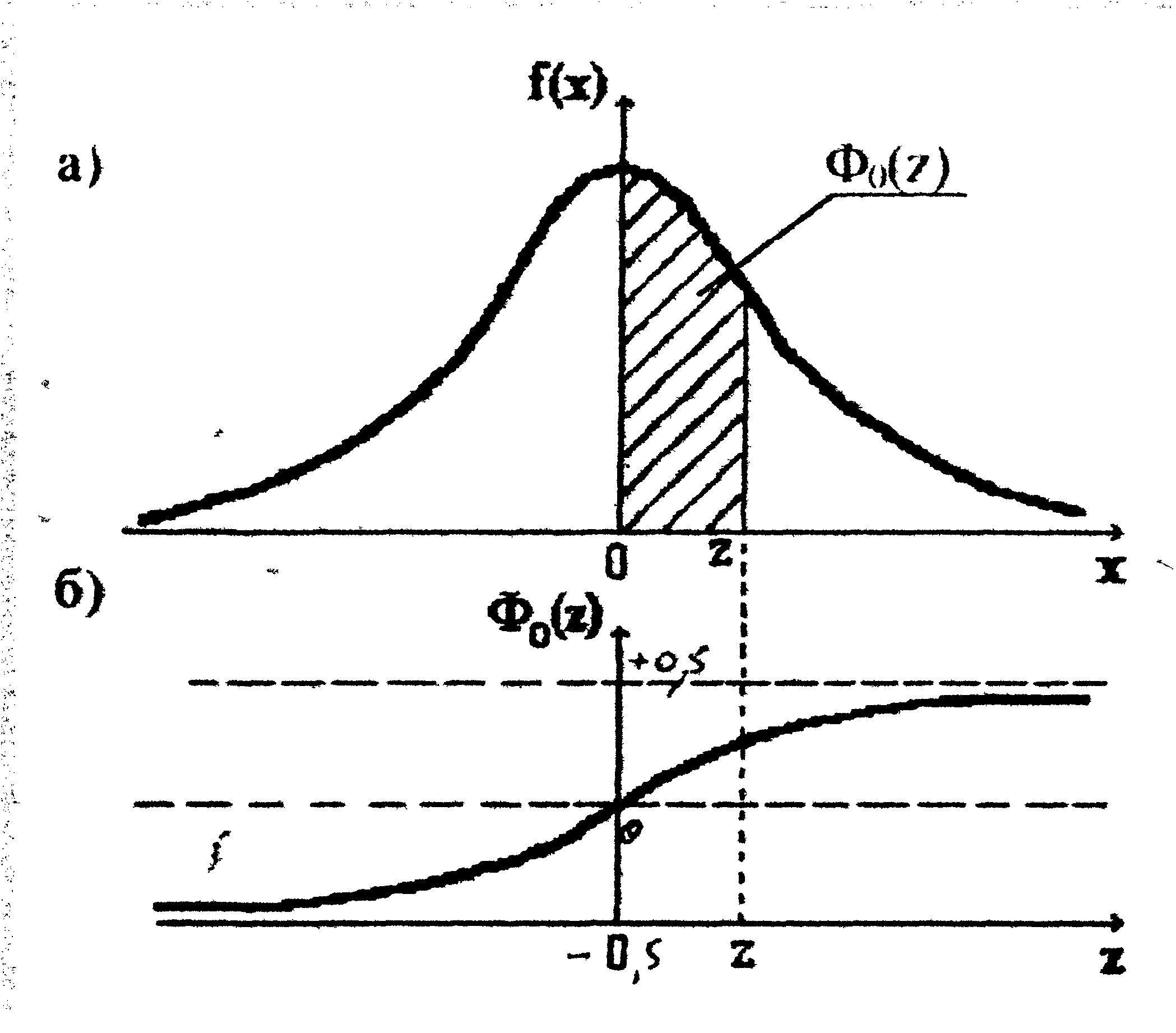
Рис. 4.7. Плотность функции нормального распределения непрерывной случайной величины (а) и нормированная функция Лапласа (б).