36.Тз с макс-ей цф

1.Нач.опор.план строится методом max тарифа

2.план перевозок – оптим-ый, кот-ым соотв-ет своб.клетки с оценками <=0

3.выбор перспект-ой клетки, кот-ый подлежит заполн-ю, должен произв-ся по полож.оценке

30. Теорема о ранге матрицы: ранг матрицы системы ограничительных уравнений ТЗ ∑nj=1 xij=ai, ∑mi=1 xij=bj , xij≥0 на единицу меньше числа уравнений (rang A= m+n-1).

Прикладное значение теоремы о ранге матрицы: кол-во занятых опорным планом клеток должно быть =m+n-1. Опорным решение ТЗ будет тогда и только тогда, когда из занятых m+n-1 клеток нельзя образовать цикл.

31. Правило «северо-западного угла»

Груз распредел. с загрузки левой верхней, условно назыв-й северо-зап., Если а₁>b₁, то х₁₁=b и первый потреб-ль будет полностью удовл. В дальн первый столбец табл в расчет не приним, в нем перем x_i1=0(i= ). Двигаясь вправо по перв строке табл, заносим в кл-ку (1;2) меньш из чисел a₁ –b₁,b₂, т.е. х₁₂=min(a₁ –b₁,b₂). Если a₁ –b₁<b₂, то х₁₂=a₁ –b₁и запасы перв пост-ка исчерп, перв строка табл в дальн в расчет не приним. Если а₁<b₁, то х₁₁=a₁и запас перв пост-ка будет исчерп. В дальн перв строка табл в расчет не приним, в нем перем x_1j=0(j= ). Двиг вниз по перв столбцу табл, заносим в кл-ку (2;1) меньш из чисел a₂,b₁–a₁, т.е. х₂₁=min(a₂,b₁–a₁). Если b₁–a_1<a₂, тох₂₁=b₁–a₁ перв потреб-ль будет полн удовл, перв столбец табл в дальн в расчет не приним. Далее аналог. В проц заполн табл могут быть одновр исключ строка и столбец. Так бывает, когда полн исчерп запас груза и полн удовл спрос (вырожд-ная задача). В этом случ в св клетке надо запис число 0 – «нуль-загр-ку», усл счит такую клетку занят.

32.Прав «миним эл-та» (наим стоим»)

Просматр тарифы в распред-ной табл и в перв очередь заполн-ся клетка с миним знач тарифа. При этом в клетку запис-ся макс возмож знач поставки. Затем из рассмотрения исключ строку, соотв пост-ку, запасы которого полностью израсходованы, или столбец, соответствующий потребителю, спрос кот полн удовл. После этого из остав-ся клеток табл снова выбирают клетку с наим тарифом. Процесс распред закан-ся, когда все запасы пост-ков исчерп, а спрос потреб-ей полн удовл. В рез-те получ опорн план, кот должен содерж m=n-1клеток.

33. Теор о потенц. Алг теор

План ТЗ Х* явл. Оптим-м, если ему соотв-т система из m+n чисел Ui и Vj, кот. удовл-т след. Усл-м: 1) Ui+Vj=Cij, X*ij≠0; 2) ∆ij=cij-(Ui+Vj)≥0, X*ij=0 Док-во: ТЗ можно рассматр-ть как двойств. задачу к некот. исх. задачи,реш-ой на max. Каждому i-му огранич-ю ТЗ в исх. задаче соотв-т перемен. Ui,i=1,m, а j-му огранич-ю x_1j+x_2j+…+x_mj=b_j перем. Vj, j=1,n. Тогда задача имеет вид: maxφ= + 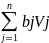, Ui+Vj≤Cij i=1,m, j=1,n Обозн. ч/з X*,Y*(Ui,Vj)-ОП двойств. исх. з-чи. На основ-ии 1-й теор. двойственности равенство: minF=maxφ. А на основании 2-й теор. двойств. выполн. усл.: 1)Ui+Vj=Cij, xij>0; 2)Ui+Vj≤Cij, xij=0, i=1,m j=1,n Из теор. след., что для ОП ТЗ необх. выполн-е усл-й: 1)кажд. занятой кл-ке в распред. табл. соотв. ∑ потенциалов, ровная тарифу этой клетки; 2)кажд. своб. кл-ке соотв-т ∑ потенц-в, не превыш-я тарифа этой кл-ке. Эк-ки оценка показ-т на сколько ден.ед. уменьш. трансп. издержки от загрузки данной кл-ки ед. груза. Алгоритм реш. ТЗ мет. потенциалов. 1)Усл.ТЗ записать в форме распред-й табл., но снач. провер. закр. или откр. модель ТЗ. 2) по 1-му из правил строим ОП. 3)Опред-м пот-лы поставщ-в и потреб-й, для этого реш-ся сист. ур-ний Ui+Vj=Cij для занятых кл-к. 4) Опред-ем оценки своб. кл-к ∆ij>0, то получим ОП единствен-й, если хотя бы 1 из оценок ∆ij=0, то имеем бесчислен. мн-во оптим. пл-в.