13.Осн теорема лп.

Если задача ЛП имеет реш, то ЦФ достигает экстрем знач хотя бы в 1 из крайн точек многогранника решений. Если же ЦФ достиг экстрем знач более, чем в 1 крайн точке, то она достиг этого же знач в люб точке, явл-ся их выпукл лин комбинацией.

Док-во: Пусть Х* - допуст реш, в кот-м ЦФ достиг своего max. Это значит, что f(X*)=maxF

Тогда f(X*)≥f(X), Xпринадлежит ОДР (1) Если Х* совпадает с 1 из крайн точек, то 1-я часть теоремы доказана. Предпол, что Х* не явл-ся крайн точкой. Следоват-но ее можно представить в виде выпукл лин комбинации крайн точек Х₁, Х₂, … ,Х_k; Х*=∑ƛ _ix_i , ƛ_i>0, i=1;k, ∑ƛ_i =1 В силу линейности ЦФ имеем: f(X*)=ƛ₁f(X₁)+ƛ₂(X₂)+ … +ƛ_kf(X_k) (2) Обозначим через М макс значение ЦФ среди всех точек М=max(f(X₁), f(X₂), … , f(X_k)) (3) Тогда из равенства (2) с условием (3) получим: f(X*) ≤ ƛ₁M+ƛ₂M+ … ƛ_kM=M→ f(X*) ≤ M (4) Из (1) и (4) можно сделать след вывод: f(X*)=М, но М – значение ЦФ в 1 из крайн точек, значит Х* совпадает с 1 из них.

12. Геом интерпр-ия задачи лп с несколькими переменными.

Перейдем к геометрической интерпретации ЗЛП с несколькими переменными.

max F = , (1)

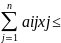b_i, (i= ), (2)

x_j 0, (j= ). (3)

Множ-во реш Х = (х₁,х₂,…,х_n), компоненты кот удовл-ют огранич-ю- равенству a_i1x₁ + a_i2x₂ +… + a_inx_in = b_i, (i=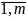 ), геом-ски пред-ют собой гиперплоскость n-мерного пространства. Это выпуклое множ-во.

Множ-во реш Х = (х₁,х₂,…,х_n), ком-ты кот удовл-ют нер-ву a_i1x₁ + a_i2x₂ +… + a_inx_in b_i, (i= ),образ полупрос-во n-мерного простр-ва, кот также явл выпуклым множ-вом.

Множ-во реш, удовл-их системе огранич задачи ЛП (2), (3) предст собой пересечение конечного числа полупространств и поэтому явл выпуклым. Теорема:Множ-во реш ЗЛП выпукло (если оно не пусто). Множ-во реш задачи ЛП в практически важных случаях чаще всего предст-ет собой либо выпуклый многогранник, либо выпуклую многогранную область. ЦФ (1) геом-ки можно рассм как семейство паралл гиперплоскостей с₁x₁ + с₂x₂ +… + с_nx_n =F, каждой из кот соот-ет опред знач параметра F. Вектор = (с₁; с₂; …;с_n), перпенд-ый к гиперплоскости F=const, указ направл наискорейшего возраст функции F. С учетом сказ задача (1)-(3) геом-ки свод. к нахождению точки Х^* = (х₁^*,х₂^*,…,х_n^*) многогранника, опред нерав-ми (2), (3), через кот проход гиперплоскость семейства (1), соот-щая наиб знач F. Граф методом можно решить ЗЛП с n>2 перем, если в ее канон-ой записи число неизв n и число линейно-независ векторов m связ соотнош-ем n-m 2.

15) Построение начальнопорн плана

Пусть з-ча ЛП представлена с мат огранич в канонич виде ∑а_ijх_j =b_i , b_i ≥0, i=1;m

Огранич-рав-во имеет предпочтит вид, если при неотриц прав части лев часть содерж перемен-ю с коэф-том=1, а в остальн ограничения эта перемен-я входит с коэф-том=0

Сис-ма огранич имеет предпочтительн вид, если кажд огранич-рав-во имеет предпочтит вид. В этом случае легко найти опорн реш( - это базисное с положит координатами)

Для этого все СП надо принять =0, а БП = свободным членам Пусть сис-ма осн огранич имеет вид: ∑а_ijх_j≤b_i , b_i ≥0, i=1;m

С пом-ю добавления клев частям дополн неотриц перемен-х дан сис-му можно привести к канонич виду: ∑а_ijх_j+ х_n+i = b_i , b_i ≥0, i=1;m

Дан сис-ма имеетпредпочтит вид и следоват-но начопорн план можно записать в виде:

Х₀=(0, 0, 0, … , 0, b₁, b₂, … , b_m)

16) Признак оптим опорн плана. Симплексн таблица Люб з-чу ЛП можно свести к виду:

maxF=∆₀ - ∑∆_jx_j

x_i+∑α_ijx_j = b_i, i=1;m

x_j≥ 0, j=1;m

Для реш з-чи запис в симплексн таблицу

Посл строку наз-ют индексн строкой или строкой ЦФ. ∆₀= С_бβ=F(X₀) – значение ЦФ для нач опорн плана Х₀; ∆_j=С_бA_j-C_j, j=m+1;n–оценки СП

Реш з-чи:1) Если з-ча на max, то план оптимальн, если ∆_j≥0, j=1;n; 2) Если з-ча на min, то план оптимальн, если ∆_j≤0, j=1;n

17. (2- альфа, В – бета, u(U) – дельта)

Сист. Осн-х огран-й имеет вид:

Х_i +Z2_ijX_j=B_i, i=1,m

Тогда нач. опорный план:

X_o=(B₁, B₂, … B_m, 0, … 0) ; U₀= F(X₀

Если u >= 0 , то Х₀ – оптим-й

Если есть j₀ , u_j<0, то Аj_{0 –} разреш-й столбец, Хj₀- перспект. Перем-я, Xi₀ – неперсп. Перем., 2i₀ j₀ – разреш-ий эл-т.

Наим-ее симпл-ое отнош-е: Q= min(B_i / 2ij₀) = Bi₀ / 2i₀ j₀ = Xj₀

Xj₀ введем в базис, Xi₀ выведем из базиса.

F(X₁) = u₀ – uj₀Q=> F(X₁) > F(X_o)

19.Теор:Если идек-й строкепосл симплек табл сод-щий опт план имеется хотя бы 1 нулевая оценка соот-я СП,то задача ЛП имеет бескон-е мн-во опт-х планов.

След-е:Если в индекс-й строке симпл-ой табл сод-я опти-й план все оценки СП полож-ны, то найд-й оптим-й план единст-й

20.Теор:Если в индеек-й строке симплек-й табл задачи ЛП на max содер-я отриц оценки,а в соот-ем столбце нет ниодного полож-о эл-та,то ЦФ на мн-ве допуст-х планов задачи неогран-на сверху.

Теор: Если в индеек-й строке симплек-й табл задачи ЛП на min содер-я полож-е оценки,а в соот-ем столбце нет ниодного полож-о эл-та,то ЦФ на мн-ве допуст-х планов задачи неогран-на снизу.