Вычисление определенного интеграла

Правда, существуют множество других численных методов для решения этой задачи, но метод Монте‑Карло, несмотря на жесткую конкуренцию, вполне заслуженно занимает свою "нишу". Эта ниша характеризуется случаем многомерных интегралов (подынтегральная функция и область интегрирования задаются многими переменными) и сравнительно невысокими требованиями к точности результатов (относительная погрешность порядка 3-10%). Это объясняется тем, что схема вычисления интеграла по методу Монте‑Карло незначительно изменяется при увеличении числа переменных, в то время как сложность традиционных численных методов возрастает комбинаторно.

Идея статистического метода вычисления определенного интеграла очень проста и основана на следующем подходе к вычислению площади геометрической фигуры. Пусть требуется определить площадь S произвольной фигуры (Рис. 5 .3). Выделим некоторую прямоугольную область с известными размерами AB, которая наверняка поглощает всю фигуру, площадь которой мы ищем. Осуществим процесс "случайного разбрасывания" N точек в пределах прямоугольной области AB (для наглядности можно представить себе "рассыпание дробинок" или чего‑нибудь в этом духе). Примем допущение, что точки располагаются хаотично, но с одинаковой вероятностью в пределах области AB. В этом случае интуитивно ясно, что число точек n, попадающих в выделенную часть области AB будет пропорционально площади этой части, то есть

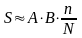
Д ля изображенного на Рис. 5 .3 примера N=26, n=9 и . Ясно, что точность такой оценки будет тем выше, чем больше число испытаний N и чем с меньшим запасом мы охватим нашу фигуру прямоугольной областью. Важной особенностью такого способа нахождения площади является его универсальность - он одинаково пригоден для фигур любой формы, в том числе и для фигур очень "замысловатой" формы.

Рис. 5.3.

Применим изложенный подход к нахождению значения определенного интеграла

значение которого, по определению, есть ни что иное, как площадь под кривой подынтегральной функции (Рис. 5 .4). Зная подынтегральную функцию f(x), зададим величину . Произведем N статистических экспериментов, каждый из которых заключается в случайном "бросании" точки в прямоугольную область, ограниченную на Рис. 5 .4 пунктирными линиями. Обозначив через n число точек, оказавшихся под кривой f(x) на интервале (a, b), можно записать формулу для оценивания величины интеграла

Для приведенного на Рис. 5 .4 примера N =50, n = 32.

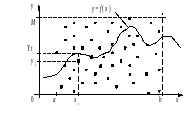
Рис. 5.4. Нахождение определенного интеграла методом Монте‑Карло

8. Генерирование псевдослучайных чисел.

8. Генерирование псевдослучайных процессов.

,

8. Построение моделей элементов сложных систем (динамическая система)

В общем случае каждый элемент модели (как динамическая система) может рассматриваться как некий "черный ящик", осуществляющий преобразование входа в выход (Рис.  6 .5). Для случая, когда и время и сама величина - непрерывны, а вход и выход являются непрерывными функциями вещественного аргумента, связь между ними может быть записана в операторной форме:

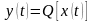. (1)

Рис. 6.5. Внешнее представление динамической системы в виде "черного ящика"

Следует подчеркнуть то, что значение выходной функции y(t) при некотором t = t₀ может зависит от всех значений функции x(t) (при ), то есть более строго следовало бы записать y(t) = Q[{x()│ _{  .}}, t].

Первое такое ограничение, которому часто удовлетворяет оператор Q –  это причинность (каузальность). Если переменная t ассоциируется с физическим временем, то условие причинности равносильно условию физической реализуемости. Смысл условия причинности состоит в том, что реакция системы в некоторый момент времени t = t₀ должна определяться только предыдущими значениями входа x(t)│_t<t0 (отклик не может начаться раньше воздействия). Для причинной системы y(t) = Q[{x()│ _{   t}}, t], что символизирует зависимость только от прошлых значений входа.

Именно это свойство лежит в основе представления причинных систем через пространство состояний.

Это представление связано с введением переменной состояния, которая ассоциируются с наличием памяти внутри системы. Модель на основе внутренних состояний (Рис.  6 .6) имеет в общем случае вид

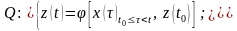(2)

где φ [,] – функция перехода состояния, η [,] – функция выхода, z(t) –  зависимость переменной состояния z от времени. Все временные функции x(t), y(t), z(t) - могут быть векторнозначными.

Представление через пространство состояний может быть выражено в дифференциальной форме через дифференциальную функцию перехода состояния ψ[,]:

Следует подчеркнуть, что дифференциальная функция перехода ψ[,], так же как и функция выходов η [,] зависят только от мгновенных значений функций‑аргументов а функция переходов φ [,] зависит от отрезка функции, то есть по первому аргументу является функционалом.

В общем случае модель на основе переменных состояния имеет структуру, показанную на Рис.  6 .6.

Рис. 6.6. Представление динамической системы в пространстве состояний

Чтобы представить систему в пространстве состояний нужно:

а) определить тип переменных состояния и их количество (размерность пространства состояний);

б) построить функции φ и η по известному оператору Q, либо по представлению через СДУ.