
- •Технология компьютерного моделирования и особенности ее применения к задачам анализа и проектирования измерительных систем (тестирование, анализ погрешности, параметрическая оптимизация)
- •Параметрическая оптимизация решается при проектировании измерительных систем сразу после определения состава необходимых блоков и связей между ними (этап структурной оптимизации).
- •Формализация понятий «модель» и «соответствие моделей»
- •Модельная трактовка задач цос и км.
- •Критерии близости моделей (погрешности соответствия )
- •Составные модели и их совокупная точность (составной оператор и композиция морфизмов).
- •Переход к конечным интервалам независимых переменных (локализация аргументов).
- •Переход к дискретным множествам для представления переменных (дискретизация по времени, квантование по уровню).
- •Реализация времени в компьютерных моделях (методы фиксированного и переменного шага).
- •Компьютерное моделирование с помощью метода статистических испытаний (метод «Монте-Карло»).
- •Вычисление определенного интеграла
- •Генерирование псевдослучайных чисел.
- •Генерирование псевдослучайных процессов.
- •Построение моделей элементов сложных систем (динамическая система)
- •Линейные динамические системы
- •Покадровый формат модели динамической системы
- •Построение моделей элементов сложных систем (конечные автоматы)
- •Построение моделей элементов сложных систем (вероятностные автоматы)
- •Построение моделей элементов сложных систем (системы массового обслуживания)
- •Модель потока заявок
- •Модель каналов обслуживания
- •Способы нахождения оценок глобальной погрешности
- •Метод «полного перебора» или «прямой» метод
- •Метод «наихудшего входного элемента»
- •Метод «статистических испытаний»
Критерии близости моделей (погрешности соответствия )
Близость двух моделей наиболее естественно определить близостью выходных результатов, которые они дают при одних и тех же входных данных. При этом нужно уточнить, что такое "при одних и тех же входных данных", а также задать способ определения расстояния между элементами множества – функцию расстояния или метрику.
Для произвольного множества A метрика ρ есть функция двух аргументов ε = ρ(x,y), x, yA, εR+, или ρ: AA R+, которая удовлетворяет двум аксиомам [Error: Reference source not found. Стр. 378]:
1) ρ(x,y) = 0 x = y, x, yA;
2) ρ(x,y)ρ(x,z)+ρ(z,y), x,y,zA (неравенство треугольника),
из которых вытекает ρ(x,y)0 и ρ(x,y) = ρ(y,x) x,yA.
В таком определении метрики для нас является важным то, что расстояние есть положительное вещественное число, определена операция сложения расстояний (аксиома 2) и сравнению подлежат только элементы одного и того же множества.
Сложность определения близости дискретно-конечной и исходной непрерывно-бесконечной модели проистекает из необходимости сравнивать между собой цифровой результат как элемент конечного множества и точный результат как элемент совершенно другого – непрерывного множества. При этом, прежде чем их сравнивать, нужно договориться, в какую одну область проецируются оба результата, а затем уже назначать правило определения расстояния между ними (метрику).
Составные модели и их совокупная точность (составной оператор и композиция морфизмов).
Рассматривается
ситуация, когда исходный оператор
проблемной области
 модельного морфизма F: M1→M2
представлен в виде композиции
модельного морфизма F: M1→M2
представлен в виде композиции

 двух операторов
двух операторов
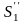 и
и
 ,
что иллюстрируется приведенной
диаграммой.
,
что иллюстрируется приведенной
диаграммой.

Такое представление часто оказывается полезным для упрощения одной сложной задачи, представляя ее в виде композиции двух, как правило, более простых. При этом важно уметь определять погрешность аппроксимации составного оператора по известным погрешностям аппроксимации частных операторов и .
С ледует
иметь в виду, что определение результирующей
погрешности всегда требует некоторой
дополнительной информации в виде знания
тех или иных компонент морфизма F.
В зависимости от того, какие из этих
компонент доступны (известны), а какие
– нет, можно рассматривать различные
варианты постановки и решения этой
задачи. Мы будем стремиться использовать
минимум информации о модели M2,
которая на момент определения погрешности
считается пока еще "не готовой",
так как мы находимся как бы "внутри"
процесса ее синтеза. После того, как
модель M2
будет построена и будет определен
морфизм F: M1→M2,
нахождение общей погрешности уже не
будет иметь принципиальных трудностей,
так для ее определения достаточно будет
воспользоваться ее формальным
определением.
ледует
иметь в виду, что определение результирующей
погрешности всегда требует некоторой
дополнительной информации в виде знания
тех или иных компонент морфизма F.
В зависимости от того, какие из этих
компонент доступны (известны), а какие
– нет, можно рассматривать различные
варианты постановки и решения этой
задачи. Мы будем стремиться использовать
минимум информации о модели M2,
которая на момент определения погрешности
считается пока еще "не готовой",
так как мы находимся как бы "внутри"
процесса ее синтеза. После того, как
модель M2
будет построена и будет определен
морфизм F: M1→M2,
нахождение общей погрешности уже не
будет иметь принципиальных трудностей,
так для ее определения достаточно будет
воспользоваться ее формальным
определением.
Отказ от использования всех необходимых исходных данных компенсируется рассмотрением множества всех возможных при этих исходных данных решений, а в качестве оценки берется величина погрешности, соответствующая "наихудшему случаю" из такого множества.
P-погрешность (локальная) R-погрешность (локальная)


Погрешности композиции
морфизмов: 
