Химические осцилляторы

1. Математическая модель и производная второй вариации энтропии

2. Изменение избытка энтропии за счёт теплообмена с окружающей средой

3. Изменение избытка энтропии за счёт массообмена с окружающей средой

4. Простая необратимая реакция

4.1. Вывод выражения для избыточного производства энтропии

4.2. Анализ устойчивости режима в реакторе

4.3. Задача о тепловой устойчивости процесса

5. Автокаталитическая реакция

5.1. Вывод выражения для избыточного производства энтропии

5.2. Анализ устойчивости режима в реакторе

6. Простая реакционная схема

6.1. Вывод выражения для избыточного производства энтропии

6.2. Анализ устойчивости режима в реакторе с помощью критерия Сильвестра

7. Реакционные схемы БелоусоваЖабо­тинского и БриггсаРаушера

7.1. Выражения для производной второй вариации энтропии

7.2. Анализ причин осцилляций

8. Осцилляторы в реакторах с рециклами

8.1. Математическое описание реактора с рециклом

8.2. Анализ влияния рецикла на устойчивость режима в реакторе

9. Классификация колебательных процессов в химии

1. Математическая модель и производная второй вариации энтропии

Рассмотрим ёмкостной проточный реактор смешения с охлаждением через рубашку, в котором могут происходить реакции типа

Математическая модель проточного реактора смешения имеет вид:

где – концентрация k-го компонента; – объёмный расход поступающего раствора; w  скорость химической реакции; Q  тепловой эффект реакции; – коэффициент теплопередачи; V  рабочий объём реактора; – поверхность реактора; – теплоёмкость, плотность и температура смеси в реакторе; – температура хладагента в рубашке; индекс (0) означает значение параметра на входе в реактор.

Поскольку реакции протекают в ёмкостном реакторе с мешалкой, в качестве необратимых процессов следует рассматривать только непосредственно химические превращения. Соотношение для производной второй вариации энтропии (5.7) при этом преобразуется к виду:

(6.1)

где – сродство химической реакции; – тепловой поток через единицу поверхности реактора; – скорость движения реакционной смеси; – химический потенциал k-го компонента; индекс n означает проекцию вектора на нормаль к поверхности реактора F_S .

Первое и второе слагаемые в правой части выражения (6.1) характеризуют изменение избытка энтропии за счёт тепло- и массообмена системы с окружающей средой, т.е. за счёт наличия протока через реактор и теплообмена через поверхность реактора с хладагентом в рубашке; таким образом, эти слагаемые определяются только конструкционными особенностями реактора. Последнее слагаемое является избыточным производством энтропии; оно зависит от типа химических превращений, протекающих в реакторе.

Напомним, что вторая вариация энтропии является термодинамической функцией Ляпунова для систем, удалённых от равновесия, и согласно второму методу Ляпунова производная этой функции должна быть положительной, чтобы стационарное состояние системы было устойчивым. Однако даже при отсутствии возможности рассчитать величину в выражении (6.1) простой анализ знаков отдельных слагаемых позволяет сделать важные выводы о том, какие процессы дестабилизируют систему (описывающие их члены в выражении (6.1) будут всегда отрицательны), а какие, наоборот, – повышают её устойчивость (описывающие их члены – всегда положительны), и как необходимо изменить условия протекания процесса, чтобы ослабить влияние первых и усилить влияние вторых.

2. Изменение избытка энтропии за счёт теплообмена с окружающей средой

Получим выражение для изменения избытка энтропии проточного реактора с мешалкой за счёт обмена энергией с окружающей средой:

Вариация от величины, обратной температуре в реакторе, определяется согласно правилам дифференцирования:

Тепловой поток из реактора в окружающую среду, отнесённый к единице поверхности реактора, определяется по формуле:

Первое слагаемое в правой части этого уравнения характеризует отвод тепла через поверхность реактора за счёт теплообмена с хладагентом в рубашке; второе слагаемое – изменение теплоты реакционной смеси за счёт наличия протока через реактор.

Допуская, что температура питательного раствора и температура хладагента в рубашке – величины постоянные, получим вариацию от теплового потока :

Подставим полученные выражения для вариаций в исходную формулу:

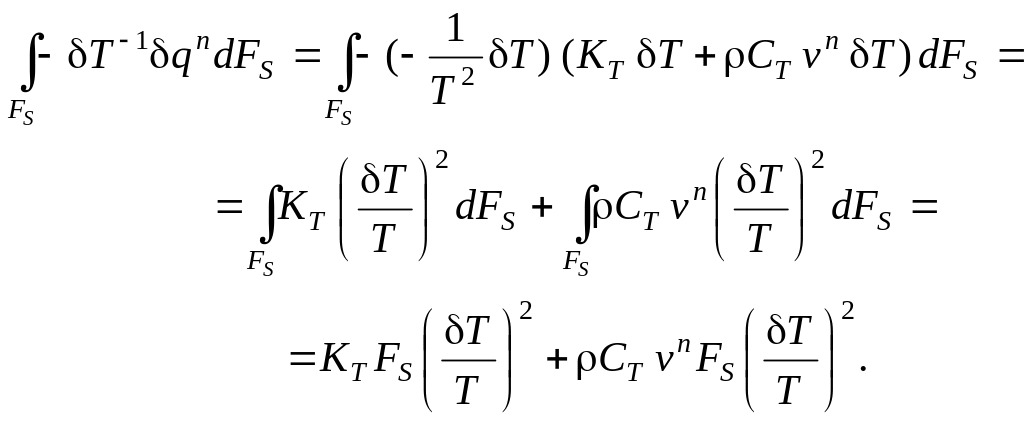
Учитывая, что

получим итоговое выражение для изменения избытка энтропии проточного реактора с мешалкой за счёт обмена энергией с окружающей средой:

(6.2)

Отметим, что выражение (6.2) определяется только типом реактора и не зависит от того, какие химические превращения в нём протекают, что позволяет его применять для любой реакционной схемы.