2 Порядок проведения работы
Схема лабораторной установки приведена на рис. 1.
2.1 Снятие статической характеристики.
Установить рукоятку ЛАТРа в положение 0 Вольт, увеличить входную величину на 10 В и каждый раз фиксировать соответствующее ей установившееся значение выходной величины.
Установившееся значение входной и выходной величин занести в таблицу 1.
Таблица 1 – Статическая характеристика
, В |
0 |
10 |
20 |
30 |
40 |
50 |
|
|
|
|
|
|
|
,
В
2.2 Снятие динамической характеристики.
Кривую разгона снять при скачкообразном изменении входной величины от 40 до 50 В (или по указанию преподавателя). Для этого следует объекту регулирования, находящемуся в состоянии динамического равновесия при = 40 В, внести скачкообразное возмущение регулирующим органом (быстро перевести его в состояние 50 В). В момент включения включить секундомер и через каждые 20 секунд фиксировать значение выходной величины до тех пор, пока она не достигнет установившегося значения. Результаты измерений занести в таблицу 2.
Таблица 2 – Динамическая характеристика
t, сек. |
20 |
40 |
60 |
80 |
…. |
…. |
Q, Cº |
|
|
|
|
|
|
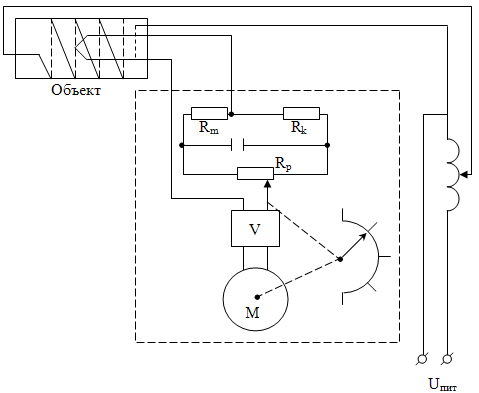
1 – регулирующий орган (ЛАТР); 2 – электрическая печь;
3 – измерительный прибор; 4 – объект регулирования
Рисунок 1 – Схема лабораторной установки
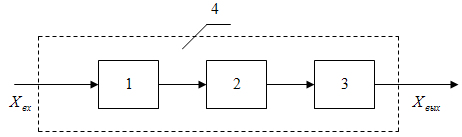
Рисунок 2 – Структурная схема регулирования
3 Обработка результатов эксперимента
3.1 Построить статическую характеристику объекта управления по данным таблицы 1.
3.2 Построить динамическую характеристику объекта управления по данным таблицы 2.
3.3. Определить статические и динамические параметры объекта.
4 Контрольные вопросы
4.1 Что представляет собой экспериментальная установка?
4.2 Устройство и принцип работы потенциометра.
4.3 Что такое кривая разгона объекта? Методика ее получения.
4.4 Что такое статическая характеристика?
4.5 В чём заключается обработка результатов эксперимента?
4.6 Какие параметры характеризуют кривую разгона? Что они характеризуют?
5 Литература
5.1. Под ред. Е.М. Душина. Основы метрологии и электрические измерения-Л.: Энергоатомиздат, 1987.
5.2. Е.К. Шевцов, М.И. Ревун. Электрические измерения в машиностроении-М.: Машиностроение, 1989.
Лабораторная работа № 4 Замена опытных данных аппроксимирующим многочленом
Цель работы: освоить замену выборки опытных данных аппроксимирующим многочленом на основе использования метода наименьших квадратов.
1 Краткие теоретические сведения
При анализе технологических измерений на практике часто возникает необходимость заменить полученные числовые выборки на функциональную зависимость.
В общем случае эта функциональная зависимость (аппроксимирующая функция) может иметь любой вид.
Предположим, что
в результате измерений получены
дискретные числовые значения величины
в зависимости от дискретных числовых
значений
,
здесь n
– число измерений.
Задача состоит в
подборе непрерывной аналитической
функции
,
наилучшим способом заменяющей дискретную
зависимость
.
Наименьшая погрешность возникает при такой замене в случае использования метода наименьших квадратов. Метод предложен Лагранжем и математически обоснован Лапласом и Гауссом.
В данной лабораторной работе в качестве аппроксимирующей функции используются многочлены вида
или
где P(0), P(i), P(2) – подлежащие определению коэффициенты аппроксимирующего многочлена.
При использовании этих многочленов возникают ошибки
.
В соответствии с методом наименьших квадратов из всех возможных значений коэффициентов Р наиболее подходящими будут те, при которых сумма квадратов ошибок будет наименьшей, т.е.
.
(1)
Рассмотрим более подробную процедуру нахождения коэффициентов.
Для разных значений из выборки измерений и при выборе в качестве аппроксимирующего многочлена Р(0)+Р(1)х имеем ошибки
(2)
Возведём в квадрат первое уравнение системы (2)
.
Выражение для
будет иметь аналогичную структуру.
Сложив эти уравнения, получим
(3)
Для нахождения
минимума
необходимо, чтобы частные производные
по коэффициентам Р этой суммы были равны
нулю
(4)
.
(5)
В соответствии с (4) дифференцируем правую часть уравнения (3) по Р(0), имеем
. (6)
Дифференцируя по Р(1), имеем
.
(7)
Упрощая уравнения (6) и (7) и объединяя их, получим так называемую нормальную систему уравнений для определения коэффициентов Р(0) и Р(1):
.
При выборе системы
в качестве аппроксимирующего многочлена
выражения
система нормальных уравнений имеет вид
2 Варианты заданий
Значения
,
одинаковые для всех вариантов. Значения
yi
взять из приложения А.
3 Содержание отчёта
Название работы.
Цель работы.
Исходные данные.
Полученные значения коэффициентов и ошибок аппроксимации.
Графическая интерпретация результатов расчёта (график полученных многочленов и опытных точек).
Выводы.
4 Контрольные вопросы
В чём заключается сущность метода наименьших квадратов?
Что представляет собой нормальная система уравнений?
Какими другими функциями можно аппроксимировать заданную выборку?
Как определить ошибки аппроксимации?
5 Литература
Пелих С. Г., Семесенко М. П. Оптимизация линейных процессов. Киев: Высшая школа, 1977. – 192с.
Вентцель Е. С. Теория вероятностей. – М.: Изд-во физ. мат. лит-ры, 2002,-564с.
ПРИЛОЖЕНИЕ А
Таблица А.1 – Варианты заданий
|
i . |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
2,05 |
1,94 |
1,92 |
1,87 |
1,77 |
1,88 |
1,71 |
1,60 |
1,56 |
1,40 |
2 |
2,09 |
2,05 |
2,19 |
2,18 |
2,17 |
2,27 |
2,58 |
2,73 |
2,82 |
3,04 |
3 |
2,02 |
1,98 |
1,67 |
1,65 |
1,57 |
1,42 |
1,37 |
1,07 |
0,85 |
0,48 |
4 |
1,99 |
2,03 |
2,20 |
2,39 |
2,19 |
2,61 |
2,35 |
2,60 |
2,55 |
2,49 |
5 |
2,23 |
2,29 |
2,27 |
2,62 |
2,72 |
2,82 |
3,13 |
3,49 |
3,82 |
3,95 |
6 |
2,07 |
2,17 |
2,21 |
2,31 |
2,10 |
2,09 |
2,12 |
1,63 |
1,78 |
1,52 |
7 |
2,18 |
2,43 |
2,40 |
2,43 |
2,65 |
2,75 |
2,67 |
2,66 |
2,63 |
2,75 |
8 |
0,10 |
0,21 |
0,01 |
0,05 |
0,13 |
0,23 |
0,21 |
0,43 |
0,57 |
0,44 |
9 |
0,16 |
0,01 |
0,01 |
0,16 |
0,05 |
0,35 |
0,19 |
0,50 |
0,74 |
1,03 |
10 |
2,09 |
2,31 |
2,72 |
2,77 |
2,78 |
2,97 |
3,00 |
3,51 |
3,43 |
3,58 |
11 |
2,15 |
2,41 |
2,58 |
2,84 |
3,28 |
3,46 |
4,02 |
4,11 |
4,61 |
5,03 |
12 |
0,10 |
0,01 |
0,19 |
0,11 |
0,31 |
0,78 |
0,64 |
0,86 |
1,18 |
1,39 |
13 |
0,17 |
0,07 |
0,17 |
0,05 |
0,12 |
0,00 |
0,01 |
0,05 |
0,21 |
0,50 |
14 |
0,80 |
0,29 |
0,52 |
0,77 |
0,93 |
1,20 |
1,20 |
1,35 |
1,39 |
1,48 |
15 |
0,04 |
0,47 |
0,78 |
1,01 |
1,19 |
1,60 |
1,93 |
2,22 |
2,50 |
3,01 |
16 |
0,08 |
0,14 |
0,37 |
0,36 |
0,44 |
0,48 |
0,27 |
0,39 |
0,50 |
0,48 |
17 |
0,02 |
0,44 |
0,51 |
0,67 |
0,69 |
1,04 |
1,14 |
1,37 |
1,77 |
2,00 |
18 |
0,014 |
0,23 |
0,44 |
0,54 |
0,72 |
0,76 |
0,37 |
0,64 |
0,57 |
0,44 |
19 |
1,86 |
1,96 |
2,12 |
2,06 |
2,15 |
2,00 |
2,12 |
3,31 |
2,29 |
2,57 |
20 |
1,65 |
2,00 |
1,87 |
1,89 |
1,75 |
1,59 |
1,44 |
1,51 |
1,00 |
1,17 |
21 |
1,89 |
2,07 |
2,30 |
2,26 |
2,34 |
2,66 |
2,88 |
2,85 |
3,16 |
3,49 |
22 |
1,84 |
1,98 |
1,72 |
1,58 |
1,59 |
1,59 |
1,58 |
1,64 |
1,55 |
1,35 |
23 |
2,92 |
1,60 |
1,57 |
1,41 |
1,36 |
0,97 |
0,59 |
0,71 |
0,15 |
0,10 |
24 |
1,90 |
1,80 |
1,82 |
1,86 |
1,83 |
2,02 |
2,01 |
2,05 |
2,46 |
2,68 |
25 |
1,80 |
1,66 |
1,36 |
1,41 |
1,13 |
0,82 |
0,74 |
0,76 |
0,64 |
0,46 |
26 |
1,65 |
1,54 |
1,41 |
0,91 |
0,63 |
0,34 |
0,12 |
0,25 |
0,64 |
96 |
27 |
1,88 |
1,69 |
1,52 |
1,55 |
1,16 |
1,27 |
1,23 |
1,36 |
1,26 |
1,47 |
28 |
4,01 |
4,06 |
3,83 |
3,98 |
4,36 |
4,18 |
4,16 |
4,51 |
4,53 |
4,38 |
Продолжение таблицы А.1
|
i . |
|||||||||
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
1 |
1,50 |
1,26 |
0,99 |
0,97 |
0,91 |
0,71 |
0,43 |
0,54 |
0,19 |
0,01 |
2 |
3,03 |
3,45 |
3,62 |
3,85 |
4,19 |
4,45 |
4,89 |
5,06 |
5,63 |
5,01 |
3 |
0,34 |
0,30 |
0,61 |
1,20 |
1,39 |
1,76 |
2,28 |
2,81 |
3,57 |
4,06 |
4 |
2,50 |
2,52 |
2,44 |
2,35 |
2,26 |
2,19 |
2,24 |
2,34 |
1,96 |
2,19 |
5 |
4,22 |
4,48 |
5,06 |
5,50 |
5,68 |
6,19 |
6,42 |
7,04 |
7,57 |
8,10 |
6 |
1,16 |
1,07 |
0,85 |
0,56 |
0,10 |
0,25 |
0,65 |
1,06 |
1,66 |
2,01 |
7 |
2,41 |
2,24 |
2,12 |
1,74 |
1,57 |
1,17 |
0,96 |
0,83 |
0,25 |
0,01 |
8 |
0,44 |
0,83 |
0,72 |
0,81 |
1,06 |
1,41 |
1,40 |
1,70 |
1,96 |
1,91 |
9 |
1,06 |
1,49 |
1,79 |
2,03 |
2,22 |
2,50 |
2,88 |
3,21 |
3,63 |
3,90 |
10 |
3,58 |
3,54 |
3,28 |
3,90 |
3,77 |
3,81 |
4,00 |
3,97 |
4,08 |
4,08 |
11 |
5,34 |
5,86 |
6,33 |
6,81 |
7,21 |
7,67 |
8,23 |
8,68 |
9,35 |
9,93 |
12 |
1,79 |
2,02 |
2,48 |
2,93 |
3,26 |
3,91 |
4,41 |
4,91 |
5,30 |
6,00 |
13 |
0,50 |
0,86 |
1,24 |
1,47 |
1,79 |
2,25 |
2,55 |
3,18 |
3,60 |
3,93 |
14 |
1,52 |
1,71 |
1,72 |
1,87 |
1,86 |
1,89 |
2,04 |
1,73 |
2,04 |
2,03 |
15 |
3,22 |
3,71 |
4,23 |
4,78 |
5,27 |
5,75 |
6,16 |
6,76 |
7,30 |
8,00 |
16 |
0,69 |
0,50 |
0,31 |
0,37 |
0,43 |
0,33 |
0,31 |
0,09 |
0,08 |
0,03 |
17 |
2,12 |
2,47 |
2,90 |
3,50 |
3,99 |
4,06 |
4,54 |
4,99 |
5,36 |
5,99 |
18 |
0,41 |
0,30 |
0,01 |
0,03 |
0,47 |
0,68 |
0,93 |
1,28 |
1,53 |
1,93 |
19 |
2,56 |
2,86 |
2,85 |
3,03 |
3,25 |
3,08 |
3,29 |
3,67 |
3,70 |
3,85 |
20 |
0,87 |
0,47 |
0,33 |
0 |
0,34 |
0,49 |
0,81 |
1,37 |
1,72 |
2,03 |
21 |
3,88 |
4,22 |
4,45 |
4,99 |
5,36 |
5,71 |
6,51 |
6,76 |
7,35 |
8,02 |
22 |
1,33 |
1,47 |
1,50 |
1,65 |
1,62 |
1,87 |
1,61 |
1,86 |
1,84 |
1,91 |
23 |
0,22 |
0,63 |
1,07 |
1,42 |
1,68 |
2,49 |
2,57 |
3,09 |
3,40 |
4,00 |
24 |
2,85 |
2,98 |
3,30 |
3,40 |
3,90 |
4,37 |
4,65 |
5,00 |
5,42 |
6,13 |
25 |
0,30 |
0,27 |
0,22 |
0,11 |
0,02 |
0,11 |
0,11 |
0,02 |
0,03 |
0,01 |
26 |
1,50 |
1,77 |
2,24 |
2,93 |
3,17 |
3,77 |
4,42 |
4,79 |
5,50 |
6,01 |
27 |
1,72 |
1,76 |
2,00 |
2,03 |
2,35 |
2,46 |
2,88 |
3,27 |
3,68 |
3,98 |
28 |
4,76 |
4,66 |
4,82 |
4,77 |
5,12 |
5,23 |
5,40 |
5,84 |
5,84 |
6,01 |