5 Статистическая проверка гипотез

При проведении статистических исследований возникает необходимость в формулировке и экспериментальной проверке некоторых предположительных утверждений (гипотез) относительно природы или величины неизвестных параметров анализируемого процесса. Если исходные данные носят случайный характер, то и ответить можно лишь с определенной степенью уверенности, если вероятность ошибки мала, то суждения можно считать практически достоверными.

Статистическая гипотеза - это предположение о случайной величине, проверяемые по выборке (результатам наблюдений). Будем обозначать высказанные предположения (гипотезу) буквой Н. Наша цель - проверить, не противоречит ли высказанная нами гипотеза Н имеющимся выборочным данным. Процедура сопоставления высказанной гипотезы с имеющимися выборочными данными (x₁,x₂,…,x_n ) и количественная оценка степени достоверности полученного вывода называется статистической проверкой гипотез. Осуществляется такая проверка с помощью статистического критерия.

Результат сопоставления может быть отрицательным или неотрицательным. Отрицательный результат означает, что данные противоречат высказанной гипотезе, следовательно, от нее надо отказаться. Неотрицательный - данные наблюдения не противоречат высказанной гипотезе, и ее можно принять в качестве одного из допустимых решений. Однако это не означает, что высказанная нами гипотеза является наилучшей, единственно подходящей. Она лишь не противоречит имеющимся выборочным данным, таким же свойством могут обладать и другие гипотезы.

Существует множество разнообразных статистических критериев, однако, они строятся по общей логической схеме, которую можно описать следующим образом:

1. Выдвигается гипотеза Н_о, которую будем называть "основной" или "нулевой".

2. Задаются величиной уровня значимости . Принятие статистического решения всегда сопровождается некоторой вероятностью ошибочного заключения как в одну, так и в другую сторону. В небольшой доле случаев  гипотеза Н_о может быть отвергнута, в то время как на самом деле она является справедливой. Это так называемая ошибка I рода, ее вероятность равна . Или, наоборот, в какой-то небольшой доле случаев  мы можем принять нашу гипотезу, в то время как на самом деле она ошибочна, а справедливым оказывается некоторое конкурирующее с ней предположение - альтернативная гипотеза Н₁. Это ошибка II рода. При фиксированном объеме выборочных данных величина вероятности одной из этих ошибок выбирается произвольно. Обычно задаются величиной  вероятности ошибочного отторжения проверяемой гипотезы Н_о. Эту вероятность называют уровнем значимости или размером критерия. Как правило, пользуются некоторыми стандартными значениями уровня значимости (= 0,1; 0,5; 0,025; 0,01; 0,005; 0,001). Наиболее распространенной =0,05. Она означает, что в среднем в пяти случаях из ста мы будем ошибочно отвергать гипотезу Н_о при многократном использовании данного статистического критерия.

3. Задаются некоторой функцией от результатов наблюдений, которую называют критической статистикой. Она сама является случайной величиной и в предположении справедливости гипотезы Н₀ подчинена некоторому хорошо изученному закону распределения.

4. Из соответствующих таблиц распределения находятся критические точки, разделяющие всю область мыслимых значений данной статистики на три части: область неправдоподобно малых, неправдоподобно больших и естественных или правдоподобных (в условиях справедливости гипотезы Н_о) значений.

5. Подсчитывают численную величину критической статистики, подставляя в функцию выборочные данные. Если вычисленное значение принадлежит области правдоподобных значений, то гипотеза Н_о считается не противоречащей выборочным данным. В противном случае, если вычисленное значение слишком мало или слишком велико, то делается вывод, что высказанное предположение Н_о ошибочно и от него следует отказаться в пользу альтернативной гипотезы.

В регрессионном анализе проверке статистической значимости подвергаются коэффициенты регрессии и корреляции. При этом соответственно используется t-статистика и F-статистика. Здесь можно использовать следующую процедуру.

1. Выдвигаем ноль-гипотезу о том, что коэффициент регрессии b статистически незначим: Н_о: b=0 или что уравнение в целом статистически незначимо Н_о: r²=0

2. Определяется фактическое значение соответствующего критерия.

3. Сравнивается полученное фактическое значение с табличным.

4. Если фактическое значение используемого критерия превышает табличное, ноль-гипотеза отклоняется и с вероятностью (1-) принимается альтернативная гипотеза о статистической значимости коэффициента регрессии или уравнения в целом. Если фактическое значение t-критерия меньше табличного, то говорят, что нет оснований отклонять ноль-гипотезу.

Статистическая значимость коэффициента регрессии проверяется с помощью t-критерия Стьюдента. Для этого сначала необходимо определить остаточную сумму квадратов

²_ост=(y_i – ŷ_i)² (24)

и ее среднее квадратическое отклонение

= (25)

Затем определяется стандартная ошибка коэффициента регрессии по формуле:

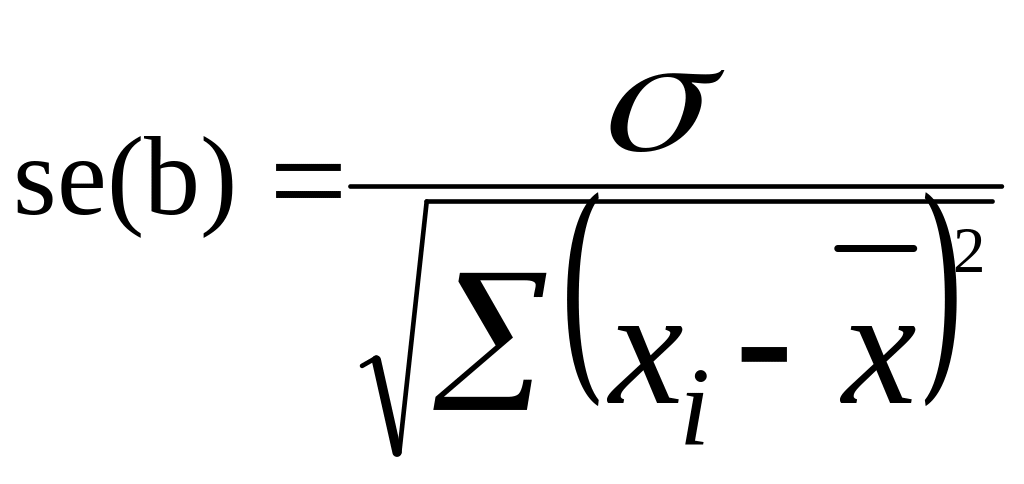(26)

Фактическое значение t-критерия Стьюдента для коэффициента регрессии рассчитывается как

. (27)

Значение |t_b|>t_кр (t_кр2 для 95% уровня значимости) позволяет сделать вывод об отличии от нуля (на соответствующем уровне значимости) коэффициента регрессии и, следовательно, о наличии влияния (связи) х и у. Малые значения t-статистики соответствуют отсутствию достоверной статистической связи между х и у.

Можно построить доверительный интервал для b. Из (27) имеем:

[b – t_кр*se(b), b + t_кр*se(b)]- 95% доверительный интервал для b.

Доверительный интервал накрывает истинное значение параметра b c заданной вероятностью (в данном случае 95%).

Оценка статистической значимости построенной модели регрессии в целом производится с помощью F-критерия Фишера. Фактическое значение F-критерия для уравнения парной регрессии, линейной по параметрам определяется как:

(28)

где ²_фактор–дисперсия для теоретических значений ŷ (объясненная вариация);

²_ост - остаточная сумма квадратов;

r²- коэффициент детерминации.

Соответственно, фактическое значение F_ф сравнивается с табличным и на основании этого сравнения принимается или отвергается ноль-гипотеза.

Вернемся к нашему примеру и сделаем соответствующие расчеты.

Выдвигаем ноль-гипотезу о том, что коэффициент регрессии статистически незначим:

H₀: b = 0. Статистическая значимость коэффициента регрессии проверяется с помощью t – критерия Стьюдента. Найдем остаточную сумму квадратов и ее среднее квадратическое отклонение:

²_ост = 2946;

 = 18,0924.

Определим стандартную ошибку коэффициента регрессии и рассчитаем фактическое значение t-критерия Стьюдента для коэффициента регрессии:

se(b) = 0,0345;

t_b = 11,3768.

Выбираем уровень значимости равным 5%. По таблице находим значение t-критерия с n-2 степенями свободы t_0,05(9) = 2,26 и сравниваем с ним фактическое значение (t_b).

Так как фактическое значение t-критерия Стьюдента превышает табличное, то ноль-гипотеза отклоняется и с вероятностью 95% принимается альтернативная гипотеза о статистической значимости коэффициента регрессии.

Далее построим 95% доверительный интервал для коэффициента регрессии b:

0,3145 < b < 0,4705.

Перейдем к расчету коэффициентов корреляции и детерминации и проверке их статистической значимости:

r = 0,9666;

d = r² = 0,9343.

Выдвигаем ноль-гипотезу о том, что уравнение регрессии в целом статистически незначимо:

H₀: r² = 0.

Оценка статистической значимости производится с помощью F- критерия Фишера. Фактическое значение F-критерия Фишера:

F_ф = 127, 9863.

По таблице находим значение F-критерия с (n-2) степенями свободы F_0,05(1,9) = 5,12 и сравниваем фактическое значение с табличным. В результате, отклоняем ноль-гипотезу и с вероятностью 95% принимаем альтернативную гипотезу о статистической значимости уравнения регрессии.