
- •080100 – «Экономика»
- •1 Общие положения
- •Основные этапы эконометрического моделирования:
- •2 Отбор факторов и показателей для построения функции потребления
- •3 Определение формы связи между результирующим (у) и объясняющим (х) факторами и расчет параметров уравнения парной регрессии
- •4 Расчет коэффициентов корреляции и детерминации, проверка правильности выбранных факторов и формы связи
- •5 Статистическая проверка гипотез
- •6 Определение и анализ эластичности потребления по доходу
- •7 Модели множественной регрессии. Построение функции потребления от двух факторов
- •Рекомендуемая литература
- •Приложение а Варианты исходных данных для выполнения лабораторной работы
3 Определение формы связи между результирующим (у) и объясняющим (х) факторами и расчет параметров уравнения парной регрессии
Задачу определения парной регрессии можно сформулировать следующим образом: по наблюденным значениям одной переменной (X) нужно оценить или предсказать ожидаемое значение другой переменной (Y).
В модели линейной регрессии теоретически предполагается существование между переменными X и Y связи следующего вида:
![]() ,
(1)
,
(1)
где y - зависимая, объясняемая переменная, результирующий признак, регрессант;
х - независимая, объясняющая переменная, регрессор, факторный признак;
U – остаточная компонента, случайный член;
, β - неизвестные параметры.
Графически модель линейной регрессии можно представить в виде, изображенном на рисунке 2.
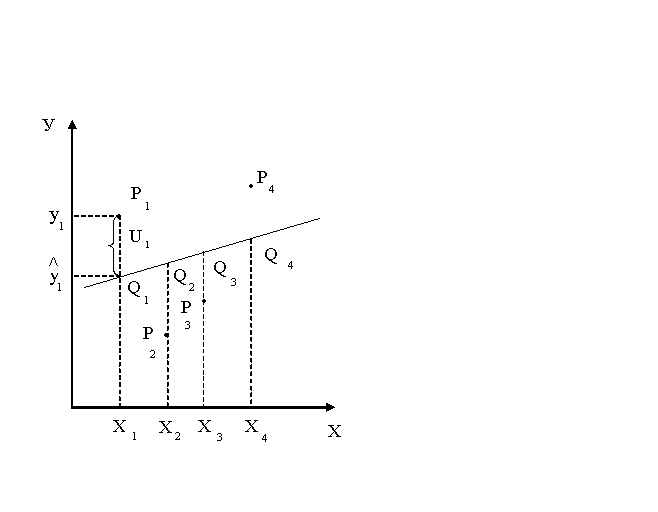
Рисунок 2 – Графическая интерпретация модели регрессии
Q1=(x1; ŷ1);
ŷ1 = a + bx1; , (2)
U1 = y1 - ŷ1. , (3)
P1, P2, P3, P4 –фактические, наблюдаемые (реальные) значения переменных X, Y;
Q1, Q2, Q3, Q4 – значения переменных в отсутствие случайного члена.
Уравнение (1) называется регрессионным уравнением. Мы имеем некоторое число пар наблюдений, характеризующих значения переменных х и у или выборку.
Задача регрессионного анализа состоит в получении оценок неизвестных параметров и β и в определении положения прямой по точкам Р (фактическим значениям). Зависимая переменная состоит из неслучайной и случайной составляющих.
Предположим, что мы нашли эти оценки и можно записать уравнение:
ŷ = a + bх, (4)
где а - регрессионная постоянная, точка пересечения линии регрессии с осью OY;
b - коэффициент регрессии, угол наклона линии регрессии, характеризующий отношение YX;
ŷ - теоретическое значение объясняемой переменной.
Используя полученное уравнение, можно рассчитать (как остатки) ei- оценки конкретных значений ошибок u в нашей выборке. Наиболее популярным методом в начальном курсе эконометрики является метод наименьших квадратов (МНК). Он позволяет получить такие оценки параметров и β, при которых сумма квадратов оценок ошибки e2 принимает минимальное значение.
Рассмотрим предполагаемую выборку, размер которой равен n, и предположим, что а и b - оценки параметров и β. В соответствии с МНК оценки а и b можно получить из условия минимизации суммы квадратов ошибок e2:
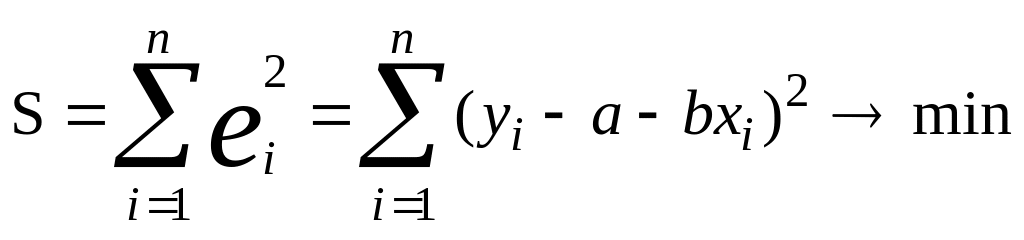 (5)
(5)
В общем случае, величину S можно рассчитать на основе выборочных наблюдений, когда уравнение регрессии описывается любой математической функцией. Для этого вычисляются алгебраические разности между наблюденными значениями Y и значениями выбранной нами функции от X, с помощью которой мы получаем оценки для Y. Это теоретические значения, обозначим их через Ŷ. Затем возводим полученные разности в квадрат и суммируем их по всем элементам выборки:
S=(yi – ŷi)2, (6)
Для выбора функции, наилучшим образом описывающей наблюденные значения, можно использовать графический метод. Исходные данные наносятся на координатную плоскость. На оси абсцисс откладывают значения факторного признака, а на оси ординат - значения результирующего признака. Расположение точек покажет примерную форму связи. Как правило, эта связь является криволинейной. Если кривизна этой линии невелика, то можно принять гипотезу о существовании прямолинейной связи.
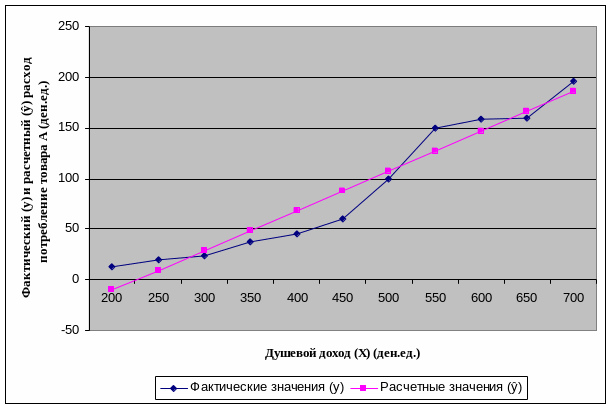
Функцию потребления можно изобразить в виде графика. Для этого в системе координат на оси абсцисс отложим значение дохода, а на оси ординат - расходы на потребление условного товара. Расположение точек, соответствующих наборам значений "доход - расход на потребление", покажет примерную форму связи (рисунок 3 а, б).
Можно рекомендовать использовать следующие функции:
y= a +bx; , (7)
y= axb, (8)
y= abx ; , (9)
![]() ,
(10)
,
(10)
МНК применяется в тех случаях, когда избранное уравнение линейно относительно своих параметров. Нелинейное уравнение следует линеаризовать.
Например:
y =abx log y= log a + xlog , (11)
y = axb log y= log a + blog x (12).
Здесь надо заметить, что графический метод определения формы связи зависимой и независимой величин часто оказывается недостаточно надёжным, поскольку визуально, по графику, почти никогда не удаётся однозначно назвать наилучшую зависимость.
а |
|
Рисунок 3 – График функции потребления
Существует более
надёжный – алгебраический – метод
определения типа кривой, особенно
удобный при расчётах на ЭВМ. Он сводится
к выявлению некоего постоянства
приращений зависимой и независимой
переменных, специфического для каждого
типа зависимости. Например, для
прямолинейной зависимости таким
постоянством является
![]() ,
для квадратической параболы – Δ2y=const,
для степенной зависимости –
,
для квадратической параболы – Δ2y=const,
для степенной зависимости –
![]() и т.д. Определив вид такого постоянства
для своего эмпирического материала (на
ЭВМ это несложно), исследователь может
быть уверен в правильности выбора формы
связи; графическая интерпретация такой
уверенности не даёт. Однако включенная
в схему логическая проверка полученных
результатов при различных формах связи
позволяет получить, как увидим далее,
вполне обоснованные результаты.
и т.д. Определив вид такого постоянства
для своего эмпирического материала (на
ЭВМ это несложно), исследователь может
быть уверен в правильности выбора формы
связи; графическая интерпретация такой
уверенности не даёт. Однако включенная
в схему логическая проверка полученных
результатов при различных формах связи
позволяет получить, как увидим далее,
вполне обоснованные результаты.
В прогнозах потребления наиболее применимы линейная и степенная формы связи. Мы исследуем обе эти формы связи.
Вначале испытываем прямолинейную зависимость вида (4). Далее следует перейти к оценке параметров выбранной функции a и b способом наименьших квадратов.
Проблема оценивания может быть сведена к "классической" задаче отыскания минимума. Переменными теперь оказываются оценки а и b неизвестных параметров предполагаемой связи у и х. Для отыскания наименьшего значения какой-либо функции сначала надо найти частные производные I порядка. Затем каждую из них приравнять нулю и разрешить полученную систему уравнений относительно переменных. В нашем случае такой функцией является сумма квадратов отклонений - S, а переменными - а и b. То есть мы должны найти = 0 и = 0 и разрешить полученную систему уравнений относительно а и b.
Выведем оценки параметров по методу наименьших квадратов, предполагая, что уравнение связи имеет вид (4). Тогда функция S имеет вид (5). Дифференцируя функцию S по а, мы получаем первое нормальное уравнение, дифференцируя по b - второе нормальное уравнение.
![]()
 ,
(13)
,
(13)
![]() ,
,
После соответствующих преобразований получим:
![]() (14)
(14)
![]()
Существуют упрощенные правила построения системы нормальных уравнений. Применим их к линейной функции:
Перемножим каждый член уравнения (4) на коэффициент при первом параметре (а), то есть на единицу.
Перед каждой переменной поставим знак суммирования.
Свободный член уравнения умножим на n.
Получим первое нормальное уравнение
Перемножим каждый член исходного уравнения на коэффициент при втором параметре (b), то есть на х.
Перед каждой переменной ставим знак суммирования.
Получаем второе нормальное уравнение
По этим правилам составляется система нормальных уравнений для любой линейной функции. Правила впервые были сформулированы английским экономистом Р. Перлом.
Параметры уравнений рассчитываются по следующим формулам:
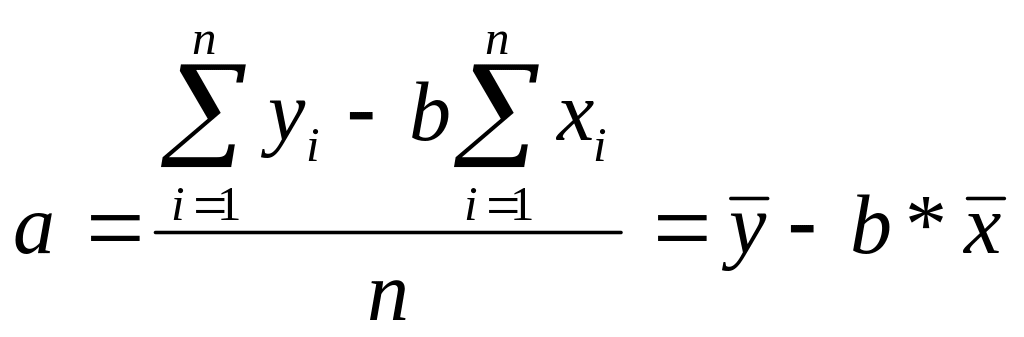 ,
(15)
,
(15)
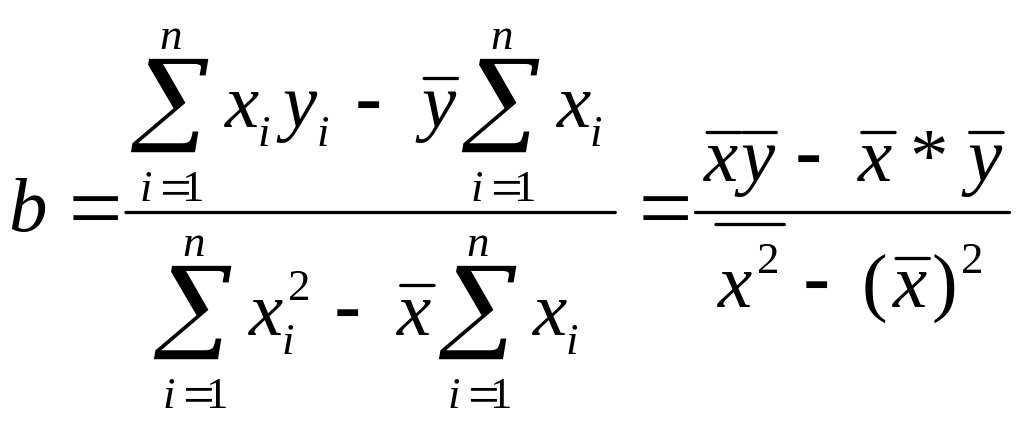 ,
(16)
,
(16)
Построим, используя исходные данные в таблице 1 , систему нормальных уравнений (14) и решим ее относительно неизвестных а и b:
9
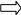 65
= 11*a
+ 4950*b a
= -88,895
65
= 11*a
+ 4950*b a
= -88,895
542200 = 4950*a + 2502500*b b = 0,3925
Уравнение регрессии имеет вид:
ŷ = -88,895 + 0,3925х, (17)
Сравним фактические и расчетные расходы на потребление товара А (таблица 2) и построим график полученной функции ŷ (рисунок 4).
 Рисунок
4- Сравнение фактических и расчетных
расходов на потребление товара А для
линейного уравнения регрессии
Рисунок
4- Сравнение фактических и расчетных
расходов на потребление товара А для
линейного уравнения регрессии
Таблица 2 - Сравнение фактических и расчетных значений расходов на потребление товара А при прямолинейной зависимости
№ группы |
Расходы на потребление товара А |
Отклонение фактических расходов от расчетных (у – ŷ) |
||
фактические (у) |
расчетные (ŷ) |
абсолютные |
относительные (в процентах) |
|
1 |
13 |
-10 |
23 |
176,92 |
2 |
20 |
9 |
11 |
55 |
3 |
24 |
29 |
-5 |
-20,83 |
4 |
38 |
48 |
-10 |
-26,32 |
5 |
45 |
68 |
-23 |
-51,11 |
6 |
60 |
88 |
-28 |
-46,67 |
7 |
100 |
107 |
-7 |
-7 |
8 |
150 |
127 |
23 |
15,333 |
9 |
159 |
147 |
12 |
7,5472 |
10 |
160 |
166 |
-6 |
-3,75 |
11 |
196 |
186 |
10 |
5,102 |
всего |
- |
- |
0 |
- |

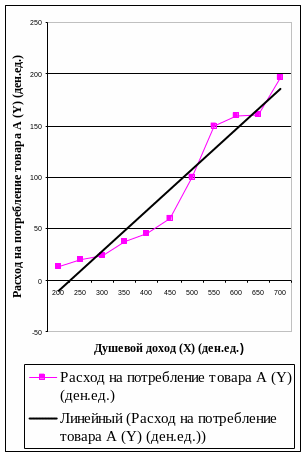
 б
б