3. Несобственный интеграл
3.1. Несобственные интегралы с бесконечными пределами
интегрирования
Пусть функция f(x)
непрерывна на промежутке a
x <+,
тогда она непрерывна на любом отрезке
[a,
b],
b
a, а
следовательно, существует определенный
интеграл EMBED Equation.3
Этот интеграл является функцией своего
верхнего предела b,
определенной на промежутке a
b <+
(рис. 3.1.1).
Рисунок 3.1.1 - Непрерывная функция на промежутке a b <+
Если при b
интеграл EMBED Equation.3
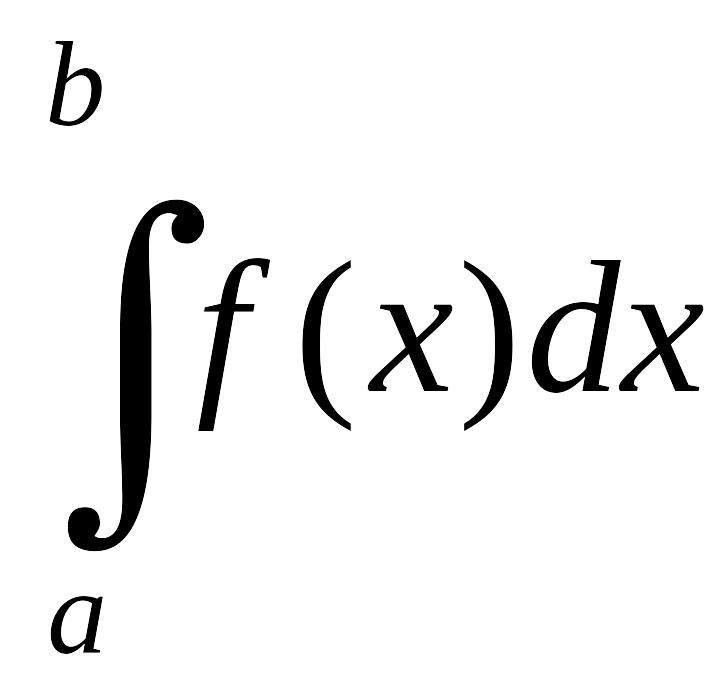стремится к конечному пределу, то этот
предел обозначают символом EMBED Equation.3
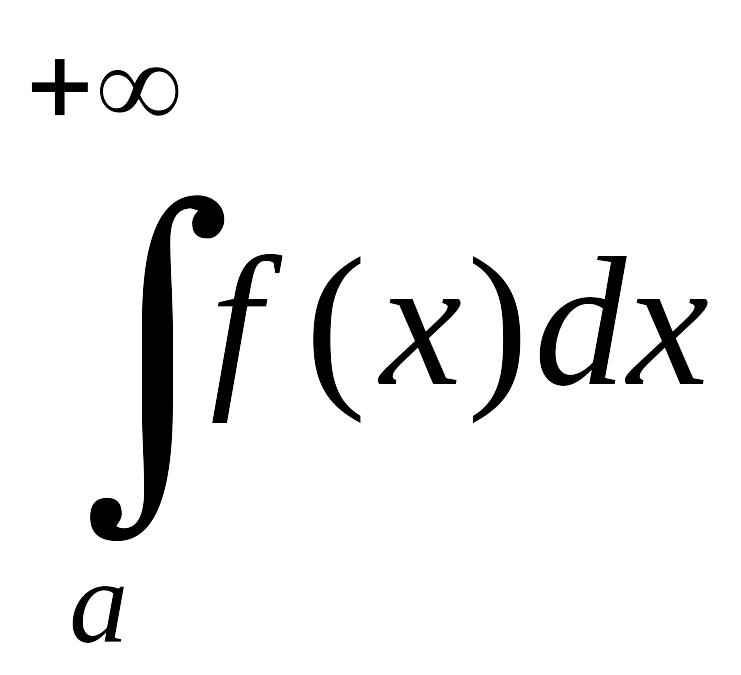и называют несобственным
интегралом с бесконечным верхним
пределом интегрирования от функции
f(x).
Таким образом, по определению несобственный интеграл с бесконечным верхним пределом интегрирования от функции f(x) вычисляется по формуле:
EMBED Equation.3
.
(3.1.1)
Если этот предел существует и конечен, то говорят, что несобственный интеграл существует или сходится.
Если же при b не существует предела интеграла EMBED Equation.3 или этот предел бесконечен, то символу EMBED Equation.3 никакого числового смысла не приписывают и говорят, что несобственный интеграл не существует или расходится.
Аналогическим
образом для функции f(x),
непрерывной на бесконечном промежутке
-
< а EMBED
Equation.3
b, определяется
несобственный интеграл EMBED Equation.3
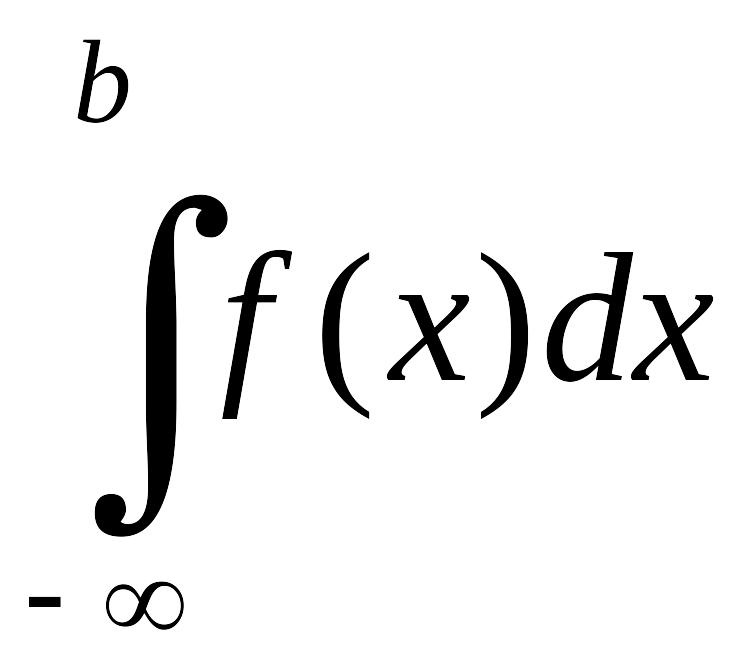(рис. 3.1.2).
SHAPE \* MERGEFORMAT
Рисунок 3.1.2 - Непрерывная функция на промежутке - < а EMBED Equation.3 b
Таким образом, по определению несобственный интеграл с бесконечным нижним пределом интегрирования от функции f(x) вычисляется по формуле:
EMBED Equation.3
.
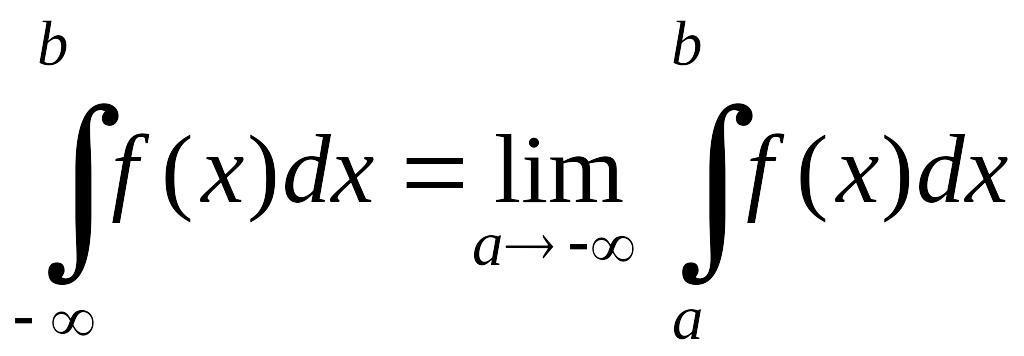(3.1.2)
Для функции f(x)
непрерывной на всей числовой оси,
несобственный интеграл EMBED Equation.3
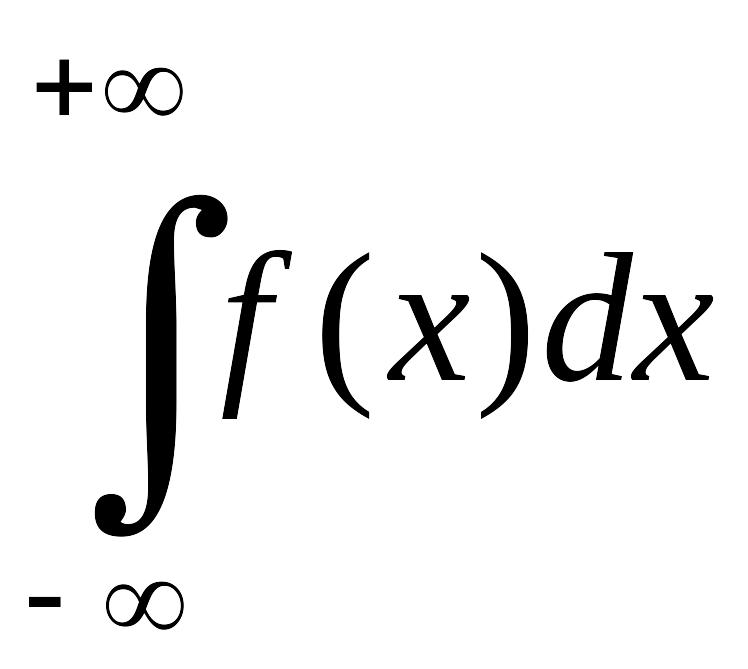называется несобственным
интегралом по бесконечному промежутку
интегрирования от функции f(x)
и вычисляется
по формуле:
EMBED Equation.3
,
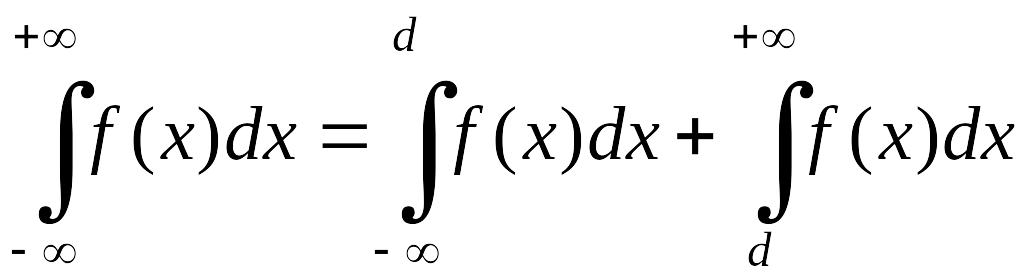(3.1.3)
где d - любое число.
Если каждый из интегралов в правой части равенства (3.1.3) сходится, то несобственный интеграл EMBED Equation.3 называется сходящимся, (причем его величина не зависит от d). Если хотя бы один из интегралов в правой части (3.1.3) расходится, то этот несобственный интеграл называется расходящимся.
Рассмотрим несколько примеров несобственных интегралов.
Пример 3.1.1.
Исследовать
сходимость
несобственного
интеграла EMBED Equation.3
.
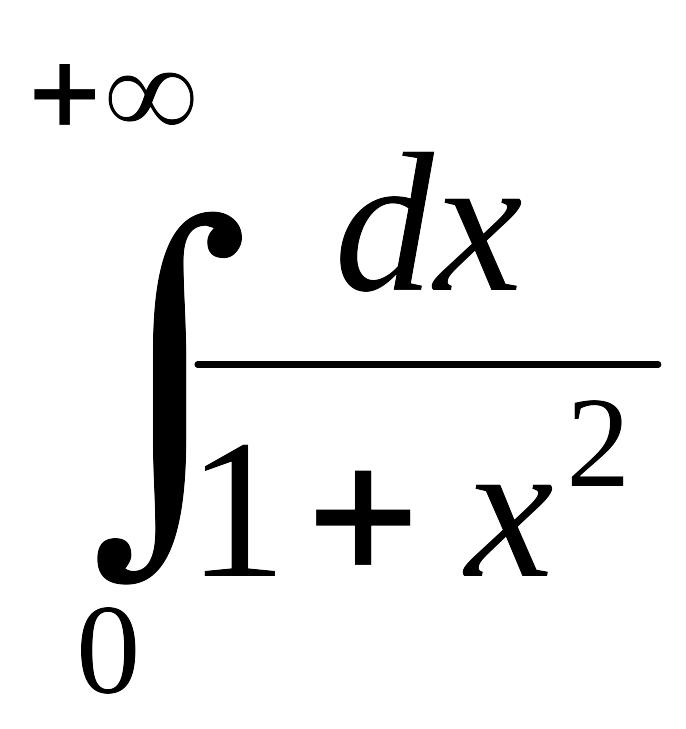Решение. По формуле (3.1.1) имеем
EMBED Equation.3
.
Поскольку этот предел существует и конечен, то данный несобственный интеграл сходится.
Пример
3.1.2. Исследовать
сходимость
несобственного
интеграла EMBED Equation.3
.
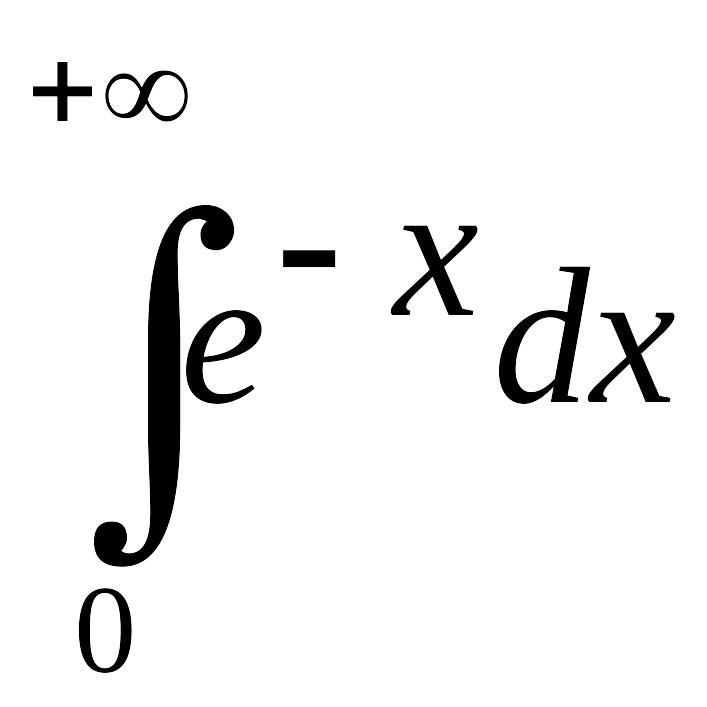Решение.
Подынтегральная
функция непрерывна в промежутке EMBED
Equation.3
,
следовательно, по формуле (3.1.1) имеем
EMBED
Equation.3
.
Поскольку этот предел существует и конечен, то данный несобственный интеграл сходится.
Замечание. Геометрический смысл несобственного интеграла тот же, что и определенного интеграла.
Так, вычислив
несобственный сходящийся интеграл
примера 3.1.2, мы получили значение площади
плоской фигуры, ограниченной графиком
функции EMBED Equation.3
,
прямой EMBED Equation.3
и осью EMBED Equation.3
(рис. 3.1.3)
SHAPE \* MERGEFORMAT
Рисунок 3.1.3 - Криволинейная трапеция
Пример 3.1.3.
Исследовать
сходимость
несобственного
интеграла EMBED Equation.3
.
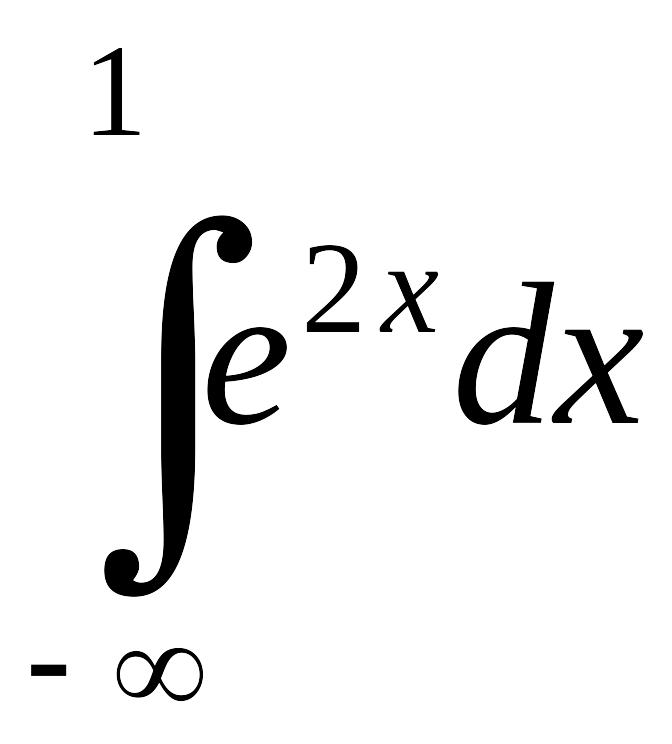Решение. По формуле (3.1.2) имеем
EMBED Equation.3
.
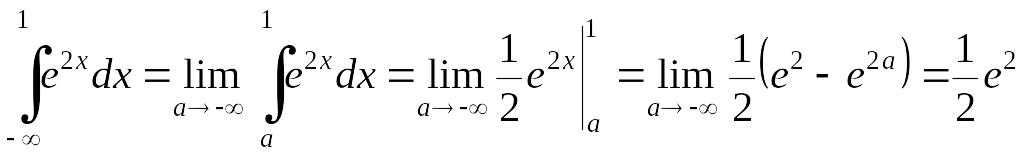Поскольку этот предел существует и конечен, то данный несобственный интеграл сходится.
Пример 3.1.4.
Исследовать
сходимость
несобственного
интеграла EMBED Equation.3
.
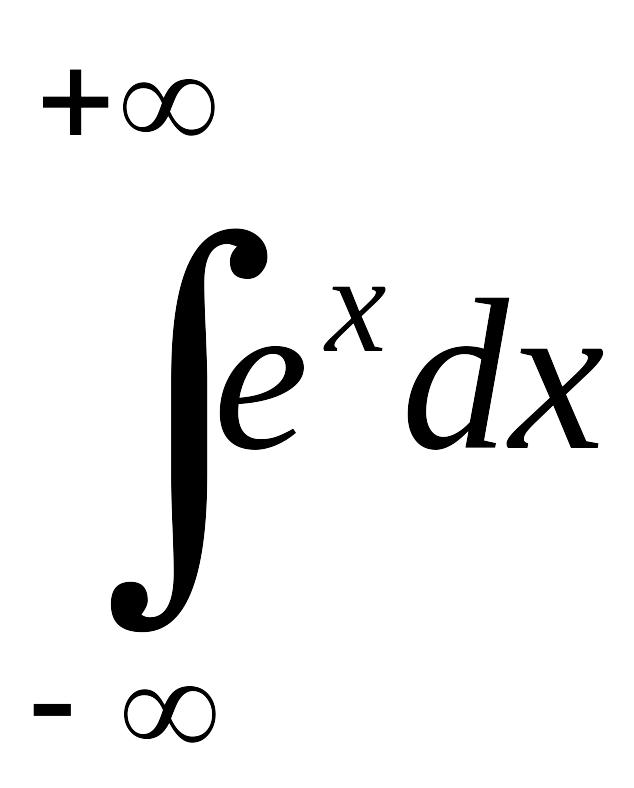Решение. В соответствии с формулой (3.1.3) имеем
EMBED Equation.3
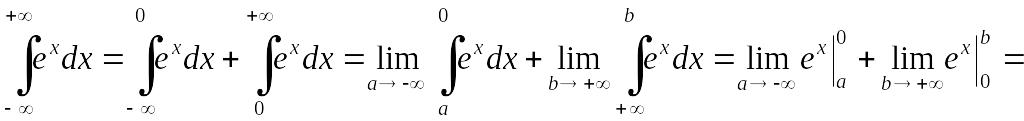
EMBED Equation.3
Поскольку этот предел равен бесконечности, то данный несобственный интеграл расходится.
Пример
3.1.5.
Исследовать сходимость
несобственного
интеграла EMBED Equation.3
.
Решение. По определению имеем:.
EMBED
Equation.3
Геометрически
данный несобственный сходящийся интеграл
выражает площадь криволинейной трапеции,
ограниченной графиком подынтегральной
функции EMBED Equation.3
и осью EMBED Equation.3
,
которая является горизонтальной
асимптотой данной функции (рис. 3.1.4).
SHAPE
\* MERGEFORMAT
Рисунок 3.1.4 - Криволинейная трапеция