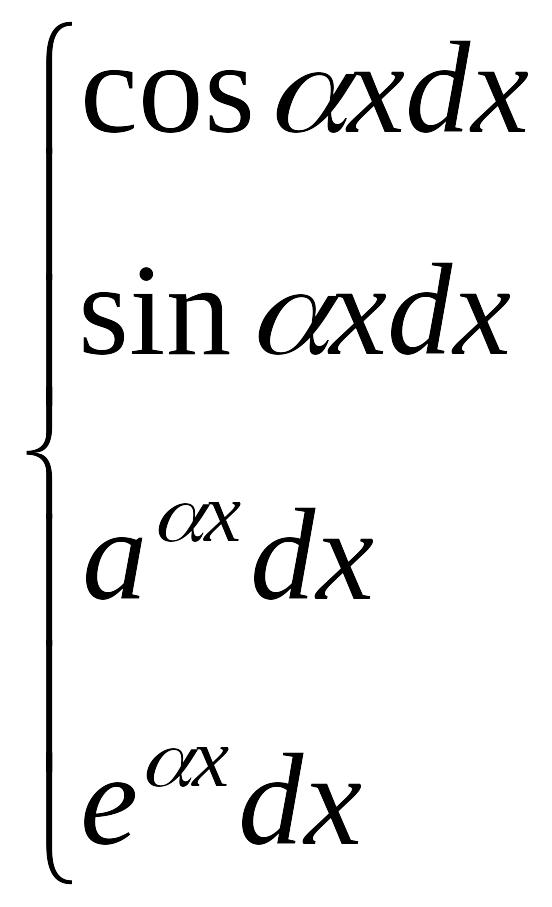1.2. Свойства определенного интеграла. Формула Ньютона–Лейбница
Рассмотрим вначале свойства, аналогичные свойствам неопределенного интеграла.
1. Постоянный множитель можно выносить за знак определенного интеграла
,
(1.2.1)
где k – некоторое число.
2. Определенный интеграл от алгебраической суммы двух функций f1(x), f2(x) равен такой же алгебраической сумме определенных интегралов от каждой из функций f1(x), f2(x)
.
(1.2.2)
Следствие: свойство 2 имеет место для любого конечного числа слагаемых.
Далее рассмотрим свойства, которые не имеют аналогов в случае неопределенного интеграла.
3. Определенный интеграл меняет знак на противоположный при перестановке пределов интегрирования:
.
(1.2.3)
4. Определенный интеграл от дифференциала равен длине интервала интегрирования:
.
(1.2.4)
5. Для любого отрезка [a, b] справедлива формула:
.
(1.2.5)
где с - некоторая точка, лежащая внутри или вне отрезка [a, b].
6. Если на отрезке [a, b] выполняется неравенство f1(x) f2(x), то
.
(1.2.6)
7. Если функция f(x) непрерывна на отрезке [a, b], то на этом отрезке найдется такая точка , что
.
(1.2.7)
8. Если m – наименьшее, а М – наибольшее значение функции f(x) на отрезке [a, b], то
.
(1.2.8)
9. Абсолютная величина интеграла не превосходит інтеграл от абсолютной величины подынтегральной функции
.
(1.2.9)
Если функция f(x)
непрерывна на отрезке [a,
b] и для нее
известен неопределенный интеграл
где F(x)
– первообразная функция для f(x)
на отрезке [a,
b],
то определенный интеграл равен приращению
первообразной F(x)
на отрезке [a,
b]:
.
(1.2.10)
Формула (1.2.10) называется формулой Ньютона – Лейбница.
Пример 1.2.1.
Вычислить
/
Решение. Почленно разделив числитель на знаменатель подынтегральной функции, представим данный определенный интеграл в виде суммы двух определенных интегралов:
Пример 1.2.2.
Вычислить
.
Решение.
.
1.3. Методы вычисления определенных интегралов
Метод замены переменной
Часто для вычисления
определенного интеграла
полезно заменить
переменную интегрирования x
новой переменной t
при помощи подстановки x
= (t)
или t = (x).
При этом необходимо перейти от старых
пределов интегрирования a
и b
к новым пределам
и ,
которые определяются из уравнений a
= (),
b = ().
Замена переменной в определенном интеграле осуществляется по формуле
.
(1.3.1)
Формула (1.3.1) называется формулой замены переменной в определенном интеграле.
Замечание. При вычислении определенного интеграла с помощью метода замены переменной возвращаться к старой переменной не следует.
Пример 1.3.1.
Вычислить
.
Решение. Переходим
к новой переменной интегрирования,
полагая x =
t2.
Найдем новые пределы интегрирования:
поскольку а
= 0,
то
;
поскольку b
= 4,
тогда
.
Найдем dx =
2tdt.
Тогда по формуле (1.3.1), получаем
=
=
.
Пример 1.3.2.
Вычислить
Решение.
Так как под знаком интеграла стоит
рациональная функция от тригонометрических
функций
и
,
то для вычисления определенного интеграла
следует использовать универсальную
тригонометрическую
подстановку
которая сведет его к интегралу рациональной
дроби.
EMBED Equation.3
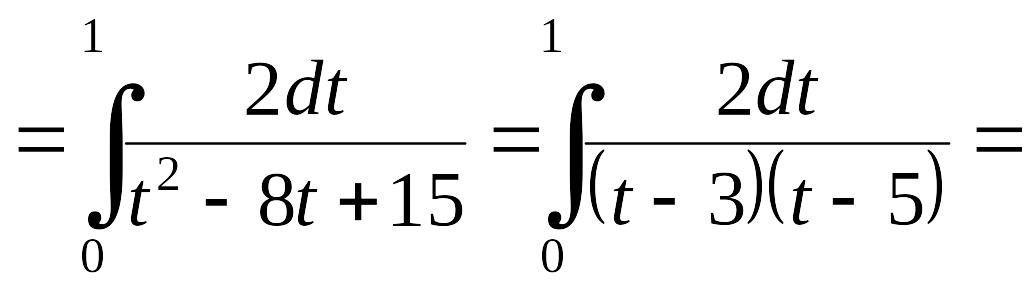EMBED Equation.3
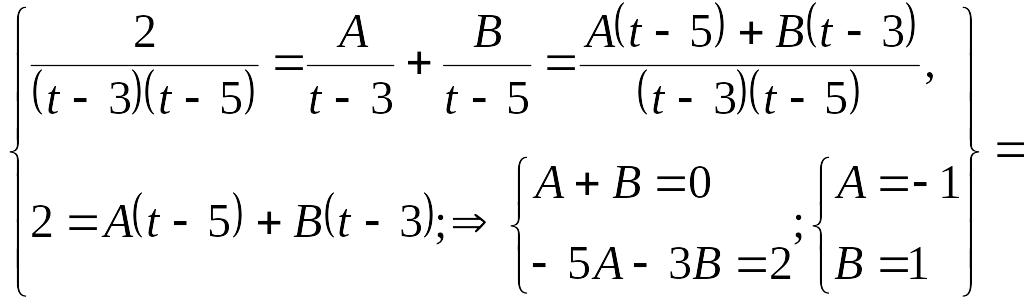
EMBED
Equation.3
.
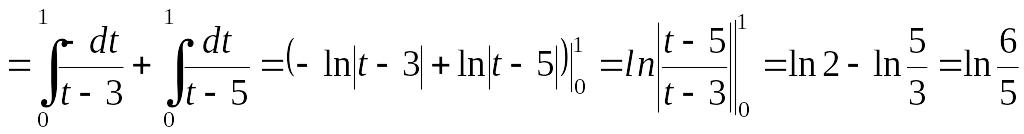Пример
1.3.3. Вычислить
EMBED
Equation.3
.
Решение.
Для вычисления данного определенного
интеграла целесообразно воспользоваться
подстановкой EMBED Equation.3
.
Такая подстановка возможна (так как при
любом значении EMBED Equation.3
под корнем получается неотрицательная
величина) и приводит к тому, что корень
под знаком интеграла исчезает.
EMBED Equation.3
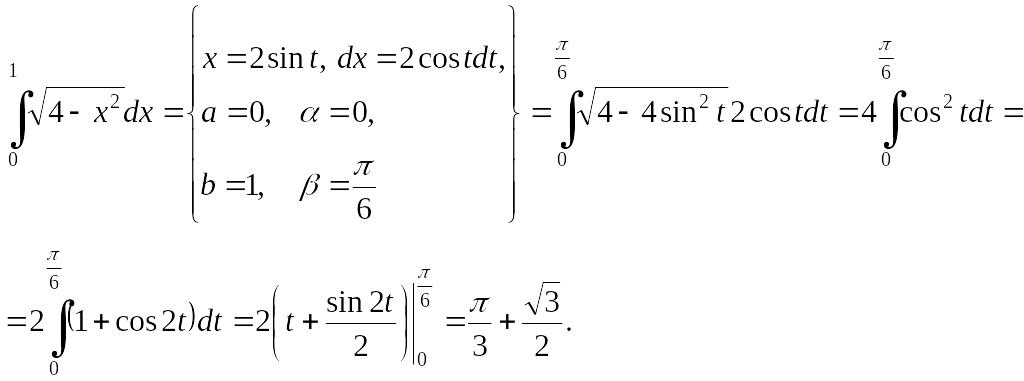
Интегрирование по частям
Если функция u(x) и v(x) обладают непрерывными производными на отрезке [a, b], то справедлива формула интегрирования по частям для определенного интеграла:
EMBED Equation.3
.
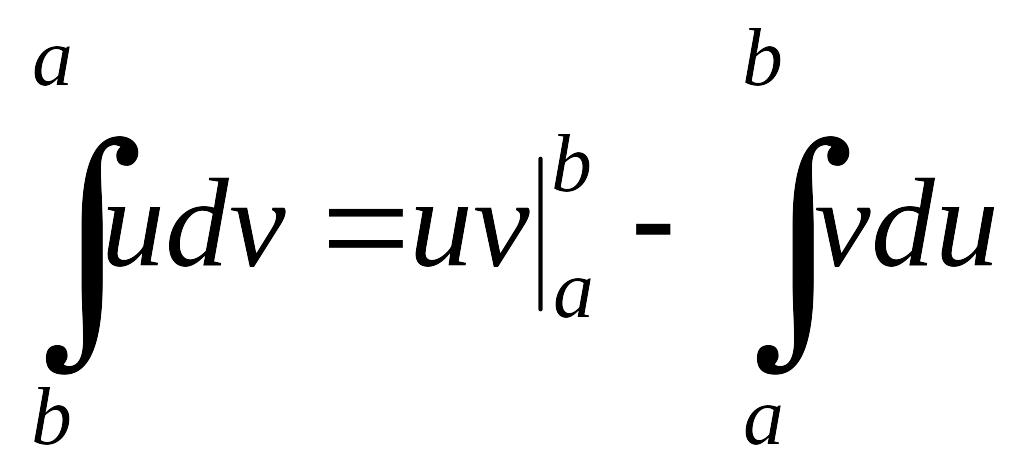(1.3.2)
Иногда формулу (1.3.2) приходится применять несколько раз.
Подынтегральное
выражение, которое составляет произведение
EMBED Equation.3
,
можно разбить на множители EMBED Equation.3
и EMBED Equation.3
несколькими способами, но следует
принять такие обозначения, чтобы интеграл
в правой части формулы (1.3.2) был более
простым, чем интеграл в левой части
этой формулы.
Замечание.
При нахождении функции EMBED Equation.3
по известному дифференциалу EMBED
Equation.3
принимается произвольная постоянная
равная нулю: С
= 0, так как
она не влияет на окончательный результат.
Можно указать некоторые типы интегралов, которые удобно вычислять, используя метод интегрирования по частям.
I. EMBED Equation.3 |
рекомендуется
обозначать: EMBED Equation.3 |
=EMBED
Equation.3
II.EMBED Equation.3 |
рекомендуется
обозначать EMBED Equation.3 |
= EMBED Equation.3
Пример 1.3.2.
Вычислить
EMBED Equation.3
.
Решение. Так как под знаком интеграла стоит произведение степенной функции на трибометрическую (первый тип), то можно использовать формулу (1.3.2.)
EMBED Equation.3
EMBED Equation.3
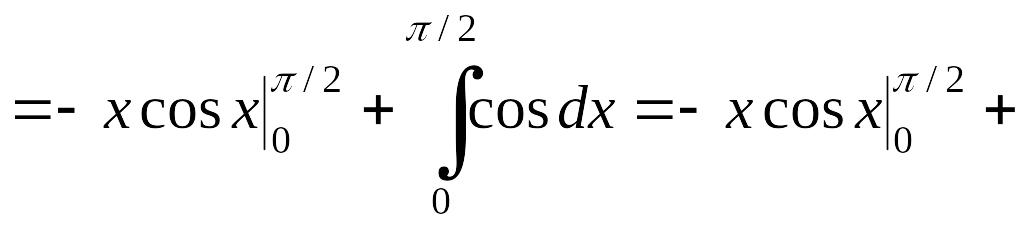
EMBED Equation.3
.
Пример 1.3.3.
Вычислить
EMBED Equation.3
.
Решение. Под знаком интеграла стоит произведение степенной функции на обратную тригонометрическую функцию (второй тип). По формуле (1.4.2.) получаем:
EMBED Equation.3
EMBED Equation.3
Пример 1.3.4.
Вычислить EMBED Equation.3
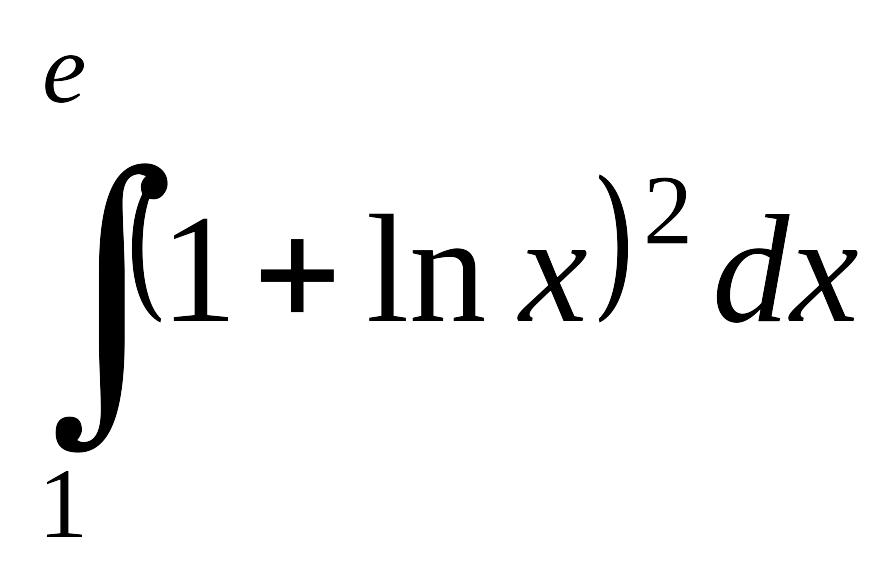
Решение. По формуле (1.4.2) получаем:
EMBED Equation.3
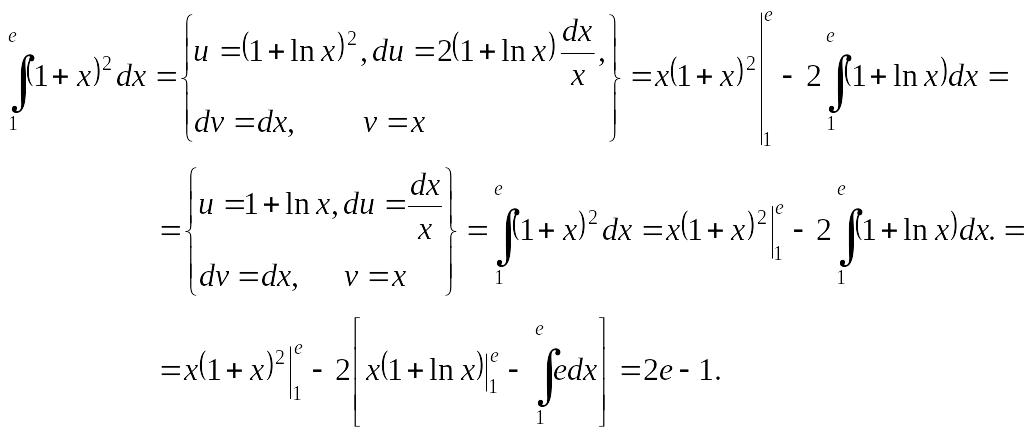
Таким образом в этом примере формула интегрирования по частям (1.4.2) была применена два раза.