Решение:

1. По значениям линейных коэффициентов парной и частной корреляции выберем неколлинеарные факторы: Х₁ и Х₃.

Рассчитаем для данных факторов коэффициенты частной корреляции:

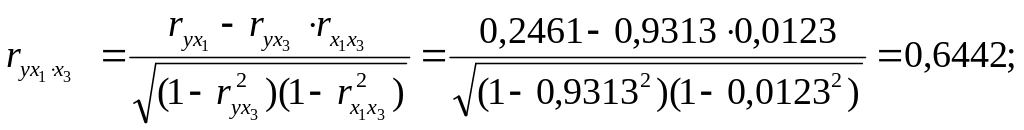
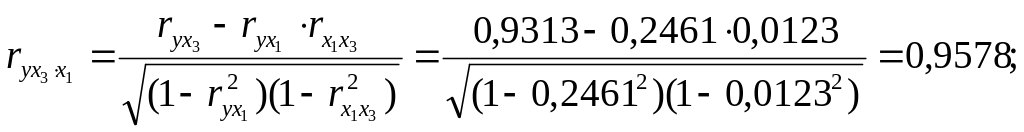
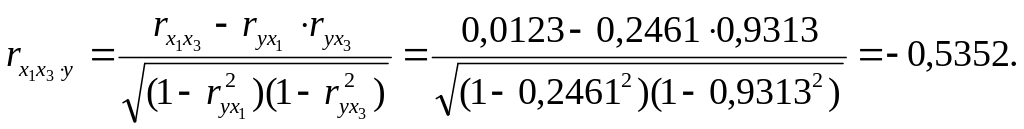
Если сравнить значения парной и частной корреляции, то приходим к выводу, что из-за слабой межфакторной связи ( ) коэффициенты парной и частной корреляции отличаются незначительно: выводы о тесноте и направлении связи на основе коэффициентов парной и частной корреляции будут совпадать:

; ; ;

; ; .

Таким образом, окончательно отбираем следующие информативные факторы во множественную регрессионную модель: Х₁ и Х₃.

2. Линейное уравнение множественной регрессии у от х₁ и х₂ имеет вид:

.

Для расчета его параметров применим метод стандартизации переменных и построим искомое уравнение в стандартизированном масштабе:

Расчет -коэффициентов выполним по формулам:

;

;

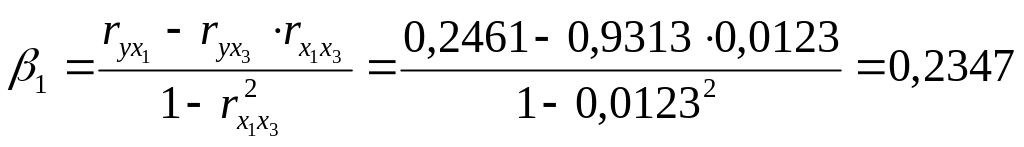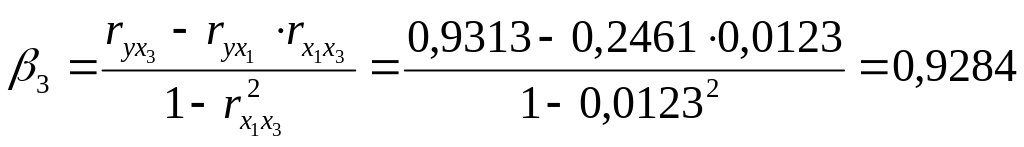Получим уравнение:

.

Очевидно, что сила влияния, х₃ на у оказалась большей, чем сила влияния х₁, к данному выводу о силе связи приходим при сравнении модулей значений и :

.

Таким образом, Х₁ – слабо влияющий фактор, а Х₃ – сильно влияющий фактор.

3. Для построения уравнения в естественной форме рассчитаем и , используя формулы для перехода от к :

; ;

.

Значение а определим из соотношения:

.

На основе полученного уравнения можно сделать вывод. Что при увеличении только суммы кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам на 1 млрд. руб., оборот розничной торговли в среднем увеличивается на 6,25 млрд. руб., а при увеличении только годового дохода всего населения на 1 млрд. руб., оборот розничной торговли в среднем увеличивается на 0,41 млрд. руб.

Для характеристики относительной силы влияния х₁ и х₂ на у рассчитаем средние коэффициенты эластичности: ;

; .

С увеличением х₁ на 1% от ее среднего уровня у возрастает на 0,098% от своего среднего уровня; при повышении х₃ на 1% у возрастает на 0,742% от своего среднего уровня. Очевидно, что сила влияния, х₃ на у оказалась большей, чем сила влияния х₁. К аналогичным выводом о силе связи приходим при сравнении модулей значений и .

4. Расчет линейного коэффициента множественной корреляции выполним с использованием коэффициентов и :

.

Коэффициент детерминации: .

Зависимость у от х₁ и х₃ характеризуются как очень тесная, в которой 92,2% вариации результативного признака у определяется вариацией учтенных в модели факторов: х₁ и х₃. Прочие факторы, не включенные в модель, составляют соответственно 7,8% от общей вариации у.

Общий F-критерий проверяет гипотезу Н₀ о статистической значимости уравнения регрессии и показателя тесноты связи (R²=0):

;

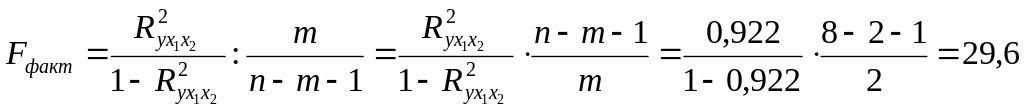F_табл = 3,4; .

Сравнивая F_табл и F_факт, приходим к выводу о необходимости отклонить гипотезу Н₀, т.к. F_табл=3,4 < F_фактл = 29,6. С вероятностью 1- делаем заключение о статистической значимости уравнения в целом и показателя тесноты связи , которые сформировались под неслучайным воздействием факторов х₁ и х₃.

5. Рассчитаем прогнозное значение результата, предполагая, что прогнозные значения факторов составят 108,5 процента от их среднего уровня, т.е. прогнозные значения факторных признаков:

(млрд. руб.)

(млрд. руб.)

тогда прогнозное значение у составит:

(млрд. руб.)