26 Ряды Лорана. Разложение аналитических функций в ряд Лорана

Рядом Лорана называется обобщённый степенной ряд, в котором наряду с положительными фигурируют и целые отрицательные степени :

Записанное выражение мы понимаем как сумму двух рядов: правильной части (обычный степенной ряд) и главной части (содержащий отрицательные степени). Пусть круг сходимости правильной части . Сделав в главной части замену , получим относительно обычный степенной ряд, у которого есть круг сходимости , т.е. . Если при этом окажется, что , то получается, что весь ряд Лорана сходится в кольце . При этом из теоремы Абеля следует, что в этом кольце ряд Лорана сходится абсолютно, а на любом замкнутом множестве, содержащемся в кольце, – ещё и равномерно. Можно доказать, что сумма ряда Лорана является в его кольце сходимости аналитической.

Имеет решение и обратная задача:

Теорема Если функция аналитическая в кольце с центром в точке , то она в этом кольце разлагается в ряд Лорана по степени .

Доказательство Пусть – любая точка этого кольца. Можно увеличить внутренний радиус кольца и уменьшить внешний радиус так, чтобы точка оставалась в новом замкнутом кольце . Границы его обозначим соответственно через и (Рисунок 40). Для замкнутого кольца верна интегральная формула Коши для многосвязных областей (параграф 18, теорема 2). Для выбранной точки

Повторяя рассуждения параграфа 22, получим разложение первого слагаемого в правильную часть ряда Лорана (ряд Тейлора):

, где

Аналогично разложим в ряд второй интеграл. Для его подынтегральной функции имеем

Мы вынесли за скобки , чтобы знаменатель геометрической прогрессии оказался по модулю меньшим единицы: (т.к. ).

Для возможности почленного интегрирования ряда по , докажем, что он на сходится равномерно. Равномерная сходимость следует из теоремы Вейерштрасса параграф 19, так как данный ряд при мажорируется числовой (т.е. не зависящей от ) положительной прогрессией , где . Интегрируя равенство, получаем

где

Складывая два полученных ряда, мы получаем разложение функции в исходном кольце в ряд Лорана.

В заключение заметим, что формулы для и отличаются только контурами интегрирования. Но ведь функция аналитична в кольце, и поэтому интегралы по этим контурам одинаковы (параграф 15). Оба они могут быть заменены интегралом по любой окружности с центром , лежащей в данном кольце. Итак, окончательно получаем:

Полученная интегральная формула для коэффициентов ряда на практике не очень удобна. Чаще всего для разложения в ряд Лорана используют известные разложения в ряд Тейлора.

Примеры

1 Функцию разложить в ряд Лорана а) в окружности точки , т.Е. По степеням ; б) в кольце в) в кольце

Так как особыми точками функции являются и 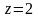, то все три указанные разложения возможны (Рисунок 41). Во всех трёх случаях используем формулу суммы геометрической прогрессии, предварительно вынося за скобки то из слагаемых в знаменателе, которое по модулю меньше другого.

а

Получился ряд Тейлора, чего и следовало ожидать, так как функция в круге аналитична.

б .

Для 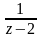можно воспользоваться предыдущим разложением, так как 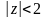. Складывая полученные разложения, получим ряд Лорана, содержащий и правильную и главную части.

в

Разложение в случае б верно и в случае в , так как

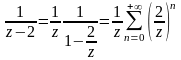
Складывая, получаем, что ряд Лорана состоит только из главной части.

2 Наибольший интерес, как мы увидим в следующих параграфах, представляет разложение функции в ряд Лорана в проколотой окрестности её изолированной особой точки. Такой точкой для функции, рассмотренной в примере 1, является, например, , а проколотая окрестность, в которой она аналитическая, имеет вид (рисунок 42) разложение же будет по степеням :

З десь главная масть ряда состоит из одного слагаемого.

27 Классификация изолированных особых точек. Теорема Сохоцкого

В примере параграфа 26 обе особые точки и являются изолированными. Однако встречаются и неизолированные особые точки. Например, для функции особыми точками являются , из которых точка не является изолированной.

Если изолированная особая точка, то существует ее проколотая окрестность, в которой функция аналитическая и, следовательно, в ней она может быть разложена в ряд Лорана но степеням . Возможны три случая:

1 в ряде Лорана отсутствует главная часть;

2 главная часть содержит конечное число членов

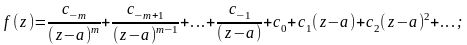
3 главная часть содержит бесконечное число членов.

В первом случае точка называется правильной (или устранимой), а функция, точнее ее аналитическое продолжение, является аналитической в точке . Во втором случае называется полюсом - го порядка (при — простой полюс). В третьем случае называется существенно особой точкой.

Примеры

1 Для функции (см. пример 3 параграф 15) точка является правильной точкой. Мы условились в параграфе 25 функцию и ее аналитическое продолжение считать одной функцией. Поэтому .

2 Для (пример 2, параграф 26) точка (и ) является простым полюсом.

3 Для функции точка существенно особая.

Исследуем, как выглядит предел функции в изолированных особых точках разного типа.

I Пусть — правильная точка, т.е. тогда в силу аналитичности, а, следовательно, непрерывности функции в точке , имеем:

II Если полюс, то

III Для случая, когда существенно особая точка, имеется следующая теорема, впервые доказанная профессором Петербургского университета Ю.В. Сохоцким (1842-1927):

Теорема 1 Если существенно особая точка функции , то для любого числа (включая ) существует такая последовательность , стремящаяся к а, что. Короче: существенно особая точка функции

Очевидно, что в существенно особой точке функция не имеет ни конечного, ни бесконечного пределов.

Пример. Мы знаем, что существенно особая точка для функции .

не существует, ибо даже на действительной оси

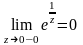
Проверьте самостоятельно, что какое бы число мы ни взяли, в любой окрестности точки найдутся точки , что .

Отвлечемся теперь ненадолго от нашей темы и выясним логический метод, называемый «обращением по разделению». Допустим, что относительно некоторого объекта возможны высказывания , причем они охватывают все возможные случая и взаимоисключают друг друга (например, ). Пусть высказывания обладают такими же свойствами, и . Тогда, как легко доказать от противного, верна серия обратных импликаций: . Например, египетский треугольник со сторонами является прямоугольным не по теореме Пифагора, а по теореме обратной к ней. Обратная же теорема легко может быть доказана методом обращения по разделению: действительно, по теореме косинусов:

треугольник прямоугольный ,

треугольник остроугольный ,

треугольник тупоугольный .

Применяя метод обращения по разделению, убеждаемся, что верны все три обратных утверждения. На этом же методе основывается доказательство следующего утверждения:

Теорема 2 Если функция в изолированной особой точке имеет конечный предел, то эта точка правильная; если бесконечный, то полюс; если нет никакого предела, то это существенно особая точка.

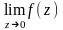Пример Рассмотрим функцию с единственной особой точ­кой . Для имеем , а для имеем . Поэтому не существует. Следовательно, точка существенно особая.