23 Оценка коэффициентов ряда Тейлора. Теорема Лиувилля. Основная теорема алгебры многочленов. Понятие кратности корня любой аналитической функции

Пусть функция аналитическая в точке . Тогда в окрестности точки она разложима в ряд Тейлора, коэффициенты которого можно задать и интегральными формулами: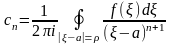 , где любое положительное число, меньшее радиуса сходности ряда. Обозначив , воспользуемся оценкой интеграла: 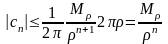. Итак

На этой оценке основывается следующая нетривиальная теорема Лиувилля:

Теорема Если функция аналитическая на всей плоскости и ограничена на ней, то она тождественно постоянная.

Например, функции и , аналитические на всей плоскости, не ограничены на ней, так как не являются постоянными (сравните с действительной областью).

Попытайтесь также ответить на вопрос: существует ли аналитическая на всей плоскости функция, отображающая плоскость на круг?

Доказательство теоремы. Пусть аналитическая на и для Тогда, разложив её в ряд 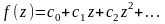в круге 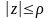, будем иметь ,гд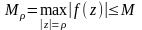е ,т.е. . Устремим к . не зависит от, и правая часть неравенства при 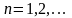стремится к нулю.

Теорема Лиувилля позволяет гораздо проще, чем в курсе алгебры, доказать основную теорему алгебры многочленов.

Теорема Гаусса Любой алгебраический многочлен положительной степени комплексными коэффициентами имеет хотя бы один комплексный корень.

Доказательство Допустим противное: (многочлен -ной степени, где 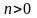) 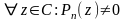. Тогда 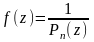аналитическая на . Докажем, что она ограничена. Очевидно 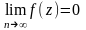а это по определению Коши означает: .Это означает, что ограничена вне круга 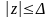.В самом круге(компакте) она тоже ограничена. Итак, ограничена и аналитична на . По теореме Лиувилля она должна быть постоянна. Тогда и 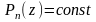, что противоречит условию .

Рассмотрим ещё одну важную связь алгебраических уравнений с рядами Тейлора. Говорят, что число является корнем многочлена 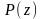кратности , если представим в ви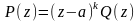де где многочлен, для которого .

Введём понятие кратности корня для любой аналитической функции . Пусть в окрестности точки разлагается в ряд Тейлора

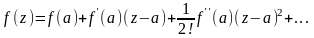
Пусть теперь 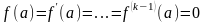, но тогда

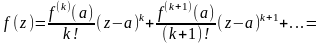
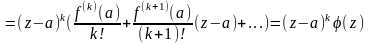
где

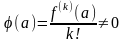
Естественно по аналогии считать, что называется корнем кратности для аналитической функции, если сама функция и все её производные до 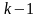- го порядка имеют в точке значения, равные нулю, a

Например, является корнем кратности 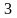для уравнения , т.к.

т .е. , но

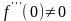
О пределите самостоятельно по графику, являются ли точки простыми корнями аналитических функций и 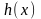соответственно.

2 4 Теорема единственности аналитической функции

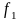Ф ункции действительной переменной, дифференцируемые в окрестности точки , допускают бесконечно много дифференцируемых продолжений за пределы этой окрестности (Рисунок 37 ). Однако, если две действительные функции и 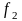разлагаются в степенной ряд в интервале и при этом совпадают в малом интервале , то они обязательно будут совпадать и на .

Действительно, обе функции в разлагаются в ряды Тейлора, но коэффициенты Тейлора, определённые лишь значениями функций в как угодно малой окрестности будут у функций одинаковы. Значит, и сами функции будут одинаковы в .

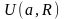Таким образом, графики двух разлагаемых в степенной ряд функций (например, цепная линия парабола) не могут сливаться между собой ни на одном даже очень малом интервале. Или, например, любая сумма степенного ряда, являющаяся линейной на части его интервала сходимости, будет линейной и на всём интервале.

Поскольку аналитические функции комплексной переменной разлагаются в степенной ряд, то для них верна более общая теорема единственности аналитической функции.

Теорема Если две функции и _,, аналитические в области , совпадают на некоторой последовательности попарно различных точек этой области, имеющей предел в , то функции совпадают во всей области.

Доказательство Обозначим, , , 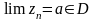тогда 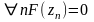Достаточно доказать:

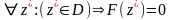
1 Так как открыто, то (Рисунок 38)

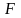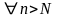
Б удучи аналитической в , функция разлагается в ней в ряд Поэтому для 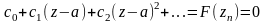Перейдём в этом равенстве к пределу. Тогда, в силу непрерывности суммы ряда, получим 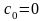.Учитывая, что все (за исключением, может быть, одного члена), мы можем разделить равенство на . Получим .Перейдя опять к пределу, получим . Продолжив этот процесс, выясним, что все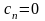 , те есть 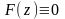в круге .

2 Так как для открытых множеств в 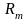связность совпадает с линейной связностью, то существует непрерывная кривая , соединяющая точки и содержащаяся в . Пусть положительное число меньшее расстояния от этой кривой до границы области . Тогда в круге .Обозначим точку пересечения границы круга с дугой через . Тогда существует последовательность 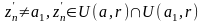такая, что . Очевидно, что 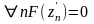. Тогда, согласно доказанному в пункте 1, имеем во всем круге

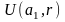
Продолжая дальше процесс покрытия дуги кругами радиуса , через конечное число шагов дойдем да такого круга, который будет содержать в себе А так как во всех кругах и .

Следствие Если две функции, аналитические в области , совпадают на любой кривой, содержащейся в , то они совпадают в .

Примеры

1 Теорема единственности позволяет многие формулы тригонометрии, доказанные в школе, например, для интервала 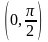действительной оси, обобщить на всю комплексную плоскость . Докажем, например, что для любого 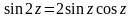.Функции 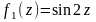и аналитические на и совпадают на интервале Согласно следствию, они должны совпадать на всем .

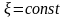2 Интересно доказательство формул, в которых фигурируют две переменные. Например, . Пусть сначала и .Тогда Формула легко доказывается по теореме единственности, как примере 1 Итак, формула доказанная для и . Пусть теперь . Тогда формула верна для .Рассматривая обе части равенства как аналитические функции от 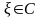и совпадающие при , мы получим их равенство при 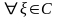вторично применяя теорему единственности.

3 Существует много разных аналитических на С функций, имеющих равные значения в точках последовательности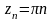 , Например, 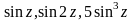и т.д. Это объясняется тем, что не имеет предела.

4 Существует ли аналитическая на функция , удовлетворяющая условию ? Поскольку последовательность сходится, то существует единственная аналитическая функция, удовлетворяющая условию. 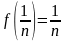Очевидно, это . Но эта функция не удовлетворяет второму условию 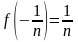. Следовательно требуемая функция не существует.

25 Понятие об аналитическом продолжении функции

Пусть область, содержащая некоторое множество 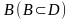, и в имеется последовательность попарно различных точек, сходящихся в Тогда, если на задана некоторая функция 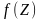, и существует в функция, совпадающая с на и аналитическая в , то эта функция называется аналитическим продолжением функции с множества на область . Из теоремы единственности следует, что если аналитическое продолжение существует, то оно единственно. Обычно его обозначают тоже буквой .

Примеры

1 Функции 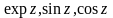аналитические на всей плоскости, можно построить разными способами (чаще всего их строят с помощью рядов). Если при этом в области действительных чисел они совпадают с одноимёнными функциями 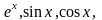то они являются единственными аналитическими продолжениями упомянутых действительных функций с на .В параграфе 9, параграфе 11 доказывается, что такое продолжение существует. Теперь мы видим, что оно единственно.

2 Функция 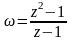аналитическая в плоскости с выколотой точкой , а функция является её аналитическим продолжением на всю плоскость.

3 Функция аналитическая везде, кроме , а соответствующий ей ряд (его сумма) 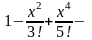… является её аналитическим продолжением на всю плоскость.

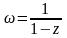4 Сумма геометрической прогрессии существует только в её круге сходимости , но функция аналитическая на всей плоскости, кроме точки . Поэтому функция . Является аналитическим продолжением суммы ряда с единичного круга на проколотую плоскость.

В примерах 2 – 4 найти аналитическое продолжение не составляло труда, так как либо сама функция, либо её продолжение были элементарными. Хуже, если функция задана рядом и не является элементарной. В этом случае существует метод Вейерштрасса аналитического продолжения (скорее умозрительный, чем практический).

Пусть функция 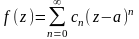с кругом сходимости ряда и пусть не все точки граничной окружности являются особыми (иначе продолжение невозможно). Причём, особые точки нам не известны.

Б ерём любую точку круга, не равную , пользуясь заданным рядом находим в ней коэффициенты Тейлора и пишем ряд Тейлора для 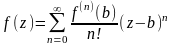. Этот ряд сходится в круге (Рисунок 39 ), радиус которого равен расстоянию от точки b до ближайшей к ней особой точки. Если этот круг выйдет за пределы предыдущего, то мы получим аналитическое продолжение функции с исходного круга на объединение кругов. Двигаясь таким образом, мы дойдём до максимально широкой естественной области аналитического продолжения, граница которой сплошь состоит из особых точек. Обычно принято считать, что аналитическое продолжение функции на максимальную область – это и есть сама функция в её естественной области определения. Такое продолжение называют полной аналитической функцией. Например, для суммы ряда соответствующей полной аналитической функцией является с областью определения \ .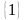