
- •1 Комплексные числа и их геометрическое представление. Предел последовательности, сумма числового ряда
- •5 Геометрический смысл модуля и аргумента производной. Конформные отображения
- •1 3 Определение интеграла и его свойств
- •16 Первообразная аналитической функции. Формула Ньютона – Лейбница
- •17 Интегральное представление логарифма
- •18 Основная формула таф (интегральная формула Коши)
- •23 Оценка коэффициентов ряда Тейлора. Теорема Лиувилля. Основная теорема алгебры многочленов. Понятие кратности корня любой аналитической функции
- •2 4 Теорема единственности аналитической функции
- •26 Ряды Лорана. Разложение аналитических функций в ряд Лорана
- •1 Функцию разложить в ряд Лорана а) в окружности точки , т.Е. По степеням ; б) в кольце в) в кольце
- •28 Вычеты. Основная теорема о вычетах
- •29 Вычисление вычетов
- •30 Примеры вычисления интегралов с помощью вычетов
- •1 Следует усвоить не готовые формулы, а метод их получения.
Введение
Ещё
в середине XVI
века математики, решая квадратные
уравнения в случае, когда дискриминант
меньше нуля, говорили, что уравнение
корней не имеет. И это было для того
времени верным утверждением, ибо мнимые
числа ещё не были известны. Но в XVI
веке итальянский математик Кардано,
один из открывателей формулы корней
кубического уравнения, обнаружил
следующий интересный факт. Опубликованная
им формула содержит квадратные корни,
и в том случае, когда под корнем оказывалось
отрицательное число, казалось бы, надо
делать вывод, что уравнение не имеет
корня. Однако Кардано взял заведомо
действительные числа
 ,
,
 ,
,
 ,
составил уравнение
,
составил уравнение
 ,
для которого эти числа являются корнями,
раскрыл в уравнении скобки, решил его
по своей формуле и опять наткнулся на
квадратный корень из отрицательного
числа. Ему ничего не оставалось делать,
как признать «законными» мнимые числа
и ввести операции над ними. С помощью
этих операций его формула и приводила,
в конце концов, к заранее известным
действительным корням.
,
для которого эти числа являются корнями,
раскрыл в уравнении скобки, решил его
по своей формуле и опять наткнулся на
квадратный корень из отрицательного
числа. Ему ничего не оставалось делать,
как признать «законными» мнимые числа
и ввести операции над ними. С помощью
этих операций его формула и приводила,
в конце концов, к заранее известным
действительным корням.
Так в математике появились мнимые числа. Однако ещё три столетия существовало недоверие к мнимым (то есть «нереальным» числам), пока Гаусс в XIX веке не привел их геометрическую интерпретацию. В настоящее время с помощью функций комплексной переменной не только получены важные результаты и для функций действительной переменной, но эти результаты приобрели определенную законченность. Функции комплексной переменной находят важные применения в аэро- и гидромеханике, в атомной физике, теории упругости, картографии, неевклидовой геометрии и так далее.
В предлагаемом курсе очень кратко, но достаточно строго излагаются основные идеи теории функций комплексной переменной. В основном они базируются вокруг теоремы и интегральной формулы Коши. Если попытаться сравнить данный курс с разработкой месторождений полезных ископаемых, то мы остановились на верхних пластах, которые дают много полезных вещей с наименьшей затратой сил.
1 Комплексные числа и их геометрическое представление. Предел последовательности, сумма числового ряда
Комплексные
числа имеют вид
 ,
где
,
где
 ,
, ,а
,а
 .
При этом
.
При этом
 называется действительной частью числа
называется действительной частью числа
 ,
а
,
а
 –
мнимой частью.
–
мнимой частью.
В алгебре определяются арифметические операции над комплексными числами так, как если бы они были двучленами, состоящими из действительных чисел. Комплексные числа равны между собой тогда и только тогда, когда равны соответственно их действительные и мнимые части.
Отношение
 между комплексными числами не определено.
между комплексными числами не определено.
Множество
всех комплексных чисел обозначается
 .
Между множествами
и
.
Между множествами
и
 существует взаимно однозначное
соответствие (Рисунок 1). Выражения
«число
»,
«точка
»
и «вектор
»
можно рассматривать как равнозначные.
существует взаимно однозначное
соответствие (Рисунок 1). Выражения
«число
»,
«точка
»
и «вектор
»
можно рассматривать как равнозначные.
В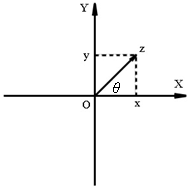
![]()

![]()
![]() ведя
полярные координаты точки
,
то есть ее модуль
ведя
полярные координаты точки
,
то есть ее модуль
 и аргумент
и аргумент
 ,
мы получим кроме алгебраической формы
записи числа
,
еще и тригонометрическую
,
мы получим кроме алгебраической формы
записи числа
,
еще и тригонометрическую
 (1)
(1)
которая
более удобна при операциях умножения,
деления и возведения в степень. Следует
отметить, что аргумент не определен для
точки
 ,
а для других точек имеет бесконечно
много (счетное число) значений. Поэтому
в случае
,
а для других точек имеет бесконечно
много (счетное число) значений. Поэтому
в случае
 мы будем называть это значение аргумента
главным и обозначать
мы будем называть это значение аргумента
главным и обозначать
 .
Для
.
Для

 ,
, (2)
(2)
Если
точка
находится
в правой полуплоскости, то, очевидно,
 .
В остальных случаях эта формула неверна,
так как множество значений арктангенса
.
В остальных случаях эта формула неверна,
так как множество значений арктангенса
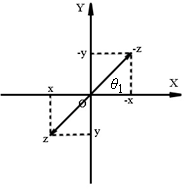
 ,
а
,
а
 .
Поэтому, если
находится во второй четверти (Рисунок
2а), то
.
Поэтому, если
находится во второй четверти (Рисунок
2а), то
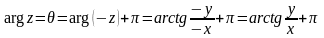 .
Если
в третьей четверти (Рисунок 2б), то
.
Если
в третьей четверти (Рисунок 2б), то

 .
Итак1:
.
Итак1:
 (3)
(3)
Из алгебры известно, что
 ,
,
 (4)
(4)
Если
 – натуральное число, то
– натуральное число, то
 ,
(5)
,
(5)
где
 – любое целое число.
– любое целое число.
Заметим,
что
 ,
где
,
где
 – любое целое число, кратное
.
Поэтому множество чисел
– любое целое число, кратное
.
Поэтому множество чисел
 не совпадает с множеством
не совпадает с множеством
 ,
а лишь является его правильной частью.
,
а лишь является его правильной частью.
Очевидно,
что
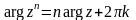 ,
где
,
где
 – некоторое (не любое) целое число,
подобранное так, что
– некоторое (не любое) целое число,
подобранное так, что
 .
.
Для модуля легко доказываются свойства:
1
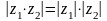 ,
,
2
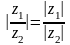 ,
,
3
 .
.
Если
 ,
,
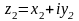 ,
то можно получить следующие формулы
для расстояния:
,
то можно получить следующие формулы
для расстояния:

Это последнее равенство весьма важно, так как оно в сочетании с алгебраическими свойствами позволяет сделать вывод:
Теорема. Множество есть линейное нормированное пространство, изоморфное евклидову пространству .
Эта теорема позволяет нам использовать все известные топологические понятия и теоремы, касающиеся , также и в , например:
1

2
 ,
так как сходимость в
равносильна сходимости по координатам.
,
так как сходимость в
равносильна сходимости по координатам.
Расширим
теперь комплексную плоскость, добавив
к ней так называемую бесконечно удаленную
точку

 ,
определив
,
определив
 -
окрестность этой точки как внешнюю
часть замкнутого круга с центром в точке
и радиусом
-
окрестность этой точки как внешнюю
часть замкнутого круга с центром в точке
и радиусом
 (Рисунок 3):
(Рисунок 3):
 ,
.
,
.
Определение
Последовательность
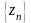 называется бесконечно большой (пишется:
называется бесконечно большой (пишется:
 или
или
 ),
если
),
если
 .
.
Это
определение, очевидно, равносильно
следующему:
 (какой бы ни была окрестность бесконечно
удалённой точки), вне ее остается лишь
конечное число членов последовательности.
(какой бы ни была окрестность бесконечно
удалённой точки), вне ее остается лишь
конечное число членов последовательности.
Примеры
1.
 ;
;
2.
 – неограниченная последовательность,
хотя и не стремится к
(т.е. не является бесконечно большой).
– неограниченная последовательность,
хотя и не стремится к
(т.е. не является бесконечно большой).
Д ля
изображения расширенного множества
комплексных чисел на ограниченном
пространстве Риман использовал
стереографическую проекцию сферы на
расширенную плоскость (Рисунок 4).
ля
изображения расширенного множества
комплексных чисел на ограниченном
пространстве Риман использовал
стереографическую проекцию сферы на
расширенную плоскость (Рисунок 4).
П
![]()
![]() усть
сфера
усть
сфера
 своим «южным полюсом» касается плоскости
своим «южным полюсом» касается плоскости
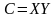 в точке
в точке
 .
Соединив каждую точку
плоскости прямолинейным отрезком с
«северным полюсом»
.
Соединив каждую точку
плоскости прямолинейным отрезком с
«северным полюсом»
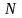 сферы, отметим на сфере точку
сферы, отметим на сфере точку
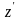 ее пересечения с отрезком. Этим
устанавливается биективное отображение
плоскости на сферу с выколотой точкой
.
Если
неограниченно
удаляется по плоскости
от начала координат
,
то
будет неограниченно приближаться к
точке
.
Поэтому естественно считать, что точке
на сфере
соответствует бесконечно удаленная
точка
на плоскости
,
а окрестности
(на сфере) – окрестность
.
ее пересечения с отрезком. Этим
устанавливается биективное отображение
плоскости на сферу с выколотой точкой
.
Если
неограниченно
удаляется по плоскости
от начала координат
,
то
будет неограниченно приближаться к
точке
.
Поэтому естественно считать, что точке
на сфере
соответствует бесконечно удаленная
точка
на плоскости
,
а окрестности
(на сфере) – окрестность
.
Сфера
Римана – компакт, а взаимно однозначное
и непрерывное отображение компакта
есть гомеоморфизм. Поэтому расширенная
плоскость
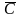 есть также компакт, гомеоморфный сфере
(хотя обычная плоскость не является
компактом).
есть также компакт, гомеоморфный сфере
(хотя обычная плоскость не является
компактом).
Напомним,
что под областью
 мы понимаем открытое связное множество,
а замкнутая область
мы понимаем открытое связное множество,
а замкнутая область
 есть область с добавленной к ней границей.
Линии и области в
можно
задавать уравнениями и неравенствами
с переменной
.
есть область с добавленной к ней границей.
Линии и области в
можно
задавать уравнениями и неравенствами
с переменной
.
Примеры
1
 – определяет окружность с центром в
точке
– определяет окружность с центром в
точке
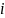 и радиусом 2;
и радиусом 2;
2
 – открытый круг;
– открытый круг;
3
 – серединный перпендикуляр к отрезку
с концами в точках
– серединный перпендикуляр к отрезку
с концами в точках
 и
и
 .
.
В комплексной плоскости сохраняются определения сходящегося числового ряда и его суммы, критерий сходимости геометрической прогрессии и формула ее суммы:
 ,
при
,
при
 .
.
Верна также теорема.
Теорема. Если сходится ряд, составленный из модулей членов данного ряда, то сходится и данный ряд.
В этом случае ряд называется абсолютно сходящимся. Для таких рядов верен, например, переместительный закон сложения, возможно также перемножение рядов.
2
![]() Функция, ее геометрический смысл. Предел
и непрерывность функции
Функция, ее геометрический смысл. Предел
и непрерывность функции
Пусть
 ,
а
,
а
 – комплексная функция комплексной
переменной с областью определения
– комплексная функция комплексной
переменной с областью определения
 и множеством значений
и множеством значений
 .
Геометрическая функция означает
отображение множества
.
Геометрическая функция означает
отображение множества
 на множество
на множество
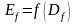 (Рисунок 5).
(Рисунок 5).
Примерами
функций являются
 ,
,
 ,
,
 ,
,
 ,
(но
,
(но
 не функция в силу многозначности
соответствия). Рассмотрим функцию
не функция в силу многозначности
соответствия). Рассмотрим функцию
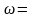
 .
Здесь
.
Здесь ,
, .
.
Для
всякой функции
 ,
записав
,
записав
 в алгебраической форме, можно выделить
ее действительную и мнимую части, т.е.
представить ее в виде
в алгебраической форме, можно выделить
ее действительную и мнимую части, т.е.
представить ее в виде
 ,
однако технически такое представление
не всегда является легкой задачей.
Интерес представляет и обратная задача.
Всякие действительные функции
,
однако технически такое представление
не всегда является легкой задачей.
Интерес представляет и обратная задача.
Всякие действительные функции
 и
и
 двух
действительных переменных можно
рассматривать и как функции от
,
а следовательно
двух
действительных переменных можно
рассматривать и как функции от
,
а следовательно
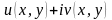 – представляет из себя комплексную
функцию переменной
.
Но даже если
– представляет из себя комплексную
функцию переменной
.
Но даже если
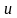 и
и
 – элементарные функции, то не всегда
– элементарные функции, то не всегда
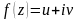 является элементарной функцией от
.
Например,
является элементарной функцией от
.
Например,
 .
Тем не менее, иногда изучение функции
.
Тем не менее, иногда изучение функции
 (даже без имеющегося ее явного выражения)
облегчает выяснение свойств ее
действительной и мнимой частей и обратно.
(даже без имеющегося ее явного выражения)
облегчает выяснение свойств ее
действительной и мнимой частей и обратно.
Сохраняются обычные определения предела и непрерывности функции в точке:
 (где
(где
 )
)
 .
.
Сформулируйте
самостоятельно, как выглядит это
определение «на языке »
(по Коши) в случаях, когда
»
(по Коши) в случаях, когда
 ,
,
 – числа или бесконечно удаленные точки,
а также определение «на языке
последовательностей» (по Гейне).
– числа или бесконечно удаленные точки,
а также определение «на языке
последовательностей» (по Гейне).
Определение.
 непрерывна в точке
непрерывна в точке
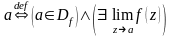
Можно
доказать, что если функция
непрерывна в точке
,
то
Для функций комплексной переменной сохраняются теоремы о пределе суммы, разности, произведения и частного, о пределе сложной функции, а также соответствующие теоремы о непрерывных функциях.
Если
функция
 непрерывна в точке
непрерывна в точке
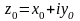 ,
то это равносильно непрерывности
и
в
точке
,
то это равносильно непрерывности
и
в
точке
 .
Действительно,
и
являются координатами точки
в плоскости
,
а сходимость в
равносильна сходимости по координатам.
.
Действительно,
и
являются координатами точки
в плоскости
,
а сходимость в
равносильна сходимости по координатам.
Примеры
1
Функция
 непрерывна на всей комплексной плоскости,
так как на ней непрерывны
непрерывна на всей комплексной плоскости,
так как на ней непрерывны
 и
и
 .
.
2
Функция
 непрерывна на
по той же причине.
непрерывна на
по той же причине.
3 Производная. Условия КРЭД
Допустим,
что функция
определена в окрестности точки
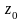 .
.
Определение. Если существует предел

то функция называется дифференцируемой в точке , а сам предел называется производной от функции в точке .
Сохраняются вместе с их доказательствами правила дифференцирования суммы, произведения и частного, степени с натуральным показателем, сложной функции, знакомые нам для функций действительной переменной. Верна также теорема.
Теорема. Всякая дифференцируемая в точке функция является в ней непрерывной.
На примере функции можно показать, что функция может быть непрерывной, но не дифференцируемой.
Рассмотрим вспомогательную функцию
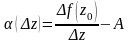 ,
,
где
 ,
т.е.
,
т.е.
 (1)
(1)
Очевидно,
что если
дифференцируема в точке
и
 ,
то
,
то
 .
И обратно, если
.
И обратно, если то функция дифференцируема в точке
и
то функция дифференцируема в точке
и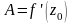 .
Этот критерий дифференцируемости
функции, аналогичный такому же для
функций действительной переменной, мы
применим для доказательства принципиально
нового критерия, присущего именно
функциям комплексной переменной
(критерий Коши-Римана-Эйлера-Даламбера).
.
Этот критерий дифференцируемости
функции, аналогичный такому же для
функций действительной переменной, мы
применим для доказательства принципиально
нового критерия, присущего именно
функциям комплексной переменной
(критерий Коши-Римана-Эйлера-Даламбера).
Теорема (критерий КРЭД). Для того, чтобы функция была дифференцируема в точке , необходимо и достаточно, чтобы функции и были дифференцируемы в точке и чтобы в этой точке выполнялись следующие условия КРЭД:

Доказательство
1 Необходимость Пусть дифференцируема в точке . Тогда из (1):
 где
где

Пусть
 ,
, ,
, .
Подставляя эти выражения в правую часть
и приравнивая действительные и мнимые
части, получим:
.
Подставляя эти выражения в правую часть
и приравнивая действительные и мнимые
части, получим:
 (2)
(2)
Обозначим
расстояние между точками
и
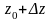 через
через
 ,
т.е.
,
т.е.
 .
Тогда
.
Тогда
 .
.
Это, в сочетании с (2), и означает, что функции и дифференцируемы в точке . Тогда, в силу единственности дифференциала, имеем для коэффициентов равенства:



Кроме того, получаем формулу:
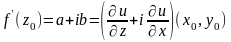
2 Достаточность Пусть функции и дифференцируемы в точке и удовлетворяют условиям КРЭД. Тогда


где,


где
 ,
Обозначим
,
Обозначим
 ,
т.е.
,
т.е.
 .
Тогда
.
Тогда

Таким образом, мы доказали, что
 ,
где
,
,
где
,
что, согласно (1), означает дифференцируемость в точке .
Примеры
1
Для функции
имеем:
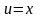 ,
,
 ;
;
 ,
,
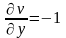 .
т.е. условия КРЭД не выполняются ни в
одной точке. Следовательно, на всей
плоскости функция не дифференцируема.
.
т.е. условия КРЭД не выполняются ни в
одной точке. Следовательно, на всей
плоскости функция не дифференцируема.
2 . Убедитесь самостоятельно, что она нигде не дифференцируема.
3
 .
Функция дифференцируема на
и
.
Функция дифференцируема на
и

4 Аналитические и гармонические функции
Определение Функция называется аналитической в точке , если она дифференцируема в некоторой окрестности этой точки.
Очевидно, что понятия аналитичности и дифференцируемости функции в области равносильны.
Примеры
1 Функция является аналитической на всей плоскости.
2
Для функции
 имеем:
имеем:

Таким
образом, условия КРЭД выполняются при
 или
или
 ,
т.е. только на координатных осях.
Следовательно, на этих осях функция
дифференцируема, но не является
аналитической.
,
т.е. только на координатных осях.
Следовательно, на этих осях функция
дифференцируема, но не является
аналитической.
Рассмотрим связь аналитических функций с так называемыми гармоническими функциями.
Пусть
 – функция распределения температур в
каждой точке замкнутой области
(пластинке).
Если теплообмен происходит только в
пределах плоскости этой пластинки, и
на её границе функция
– функция распределения температур в
каждой точке замкнутой области
(пластинке).
Если теплообмен происходит только в
пределах плоскости этой пластинки, и
на её границе функция
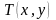 задана и не меняется во времени, то
интуитивно ясно, что и внутри области
будет в каждой точке вполне определенная
температура. В конце XVIII
в. Лаплас доказал, что температура
удовлетворяет следующему уравнению:
задана и не меняется во времени, то
интуитивно ясно, что и внутри области
будет в каждой точке вполне определенная
температура. В конце XVIII
в. Лаплас доказал, что температура
удовлетворяет следующему уравнению:

а его решение назвал гармоническими функциями, если они имеют непрерывные производные до второго порядка.
Теорема. Если аналитическая в области функция, то , – гармонические в функции.
Доказательство
Продифференцируем
первое условие КРЭД по
,
а второе – по
 и сложим результаты;
и сложим результаты;

Замечание. Можно доказать, что всякая функция, аналитическая в области, имеет в ней непрерывную производную. Поэтому в дальнейшем для облегчения некоторых доказательств (в частности, теоремы Коши параграф 15) будем под аналитической функцией понимать функцию, имеющую непрерывную производную в области. Отсюда, в частности, и из формулы (3) параграф 3 и из условий КРЭД следует непрерывность частных производных первого порядка от функций и . В дальнейшем (параграф 22) будет доказано, что всякая аналитическая в области функция имеет в ней производные любого порядка, откуда и вытекает существование и непрерывность частных производных любого порядка от , . Поэтому смешанные производные в (1) не зависят от порядка дифференцирования (теорема Шварца). Аналогично доказывается, что – функция гармоническая.
Интересно
отметить, что зная какую-нибудь
гармоническую функцию
или
,
можно почти однозначно (с точностью до
произвольной постоянной) найти парную
с ней функцию так, чтобы
 была функцией аналитической.
была функцией аналитической.
Пример. Восстановить аналитическую функцию по её мнимой части
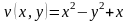
Решение Сначала убедимся, что – гармоническая функция (в противном случае задача не имеет решения):

Поскольку должна быть аналитической, то для неё должны выполнятся условия КРЭД, т.е.
 (2)
(2)
Поскольку
искомая функция
дифференцируема, то задача свелась к
восстановлению функции по известному
её полному дифференциалу
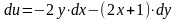 .С
такой задачей мы встречались в теории
криволинейных интегралов и теории
дифференциальных уравнений (уравнения
в полных дифференциалах).
.С
такой задачей мы встречались в теории
криволинейных интегралов и теории
дифференциальных уравнений (уравнения
в полных дифференциалах).
Проинтегрируем первое равенство (2) по :

Таким образом, искомая аналитическая функция имеет вид
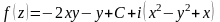 ,
,
где
 – произвольная действительная постоянная.
– произвольная действительная постоянная.
