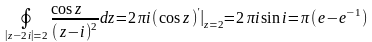18 Основная формула таф (интегральная формула Коши)

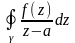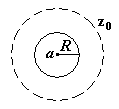
П усть аналитическая в замкнутой односвязной области , – её граница, а точка – любая внутренняя точка области . Тогда функция будет также аналитической в с выколотой точкой . Для вычисления интеграла заменим его равным по второй теореме Коши интегралом по окружности 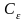являющейся границей круга , целиком лежащего внутри (рисунок 28).

(см. пример 3 параграф 14). Докажем, что интеграл в правой части равен нулю. Для этого воспользуемся оценкой интеграла (параграф 14):

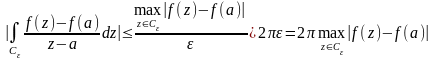
П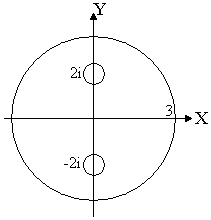 ереходя к пределу при 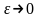(тогда для 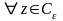), в силу непрерывности в точке получим 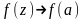. Следовательно, правая, а значит и левая части неравенства будут стремиться к нулю. Но интеграл не зависит от , поэтому он равен нулю. Итак, мы доказали формулу . Заменяя в этой формуле обозначения на , а переменную интегрирования на , мы получим следующий вывод:

Теорема 1 Если функция аналитическая в замкнутой односвязной области , ограниченной контуром , a - любая внутренняя точка этой области, то

Эта формула называется интегральной формулой Коши для случая односвязной области. Её по праву называют основной формулой ТАФ, так как практически все дальнейшие результаты данного курса будут получены как следствия из неё. Формула вскрывает любопытный факт, не имеющий аналога для дифференцируемых функций действительной переменной: если функция аналитическая в замкнутой области, то её значения внутри области полностью определяются значениями на границе. Аналогичный факт имеет место для гармоничных функций, которые являются решениями уравнения теплопроводности (Лапласа).

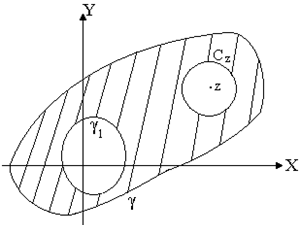
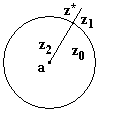
Если аналитична в многосвязной области с внешней границей и внутренними а – внутренняя точка (рисунок 29), то, окружая точку малой окружностью 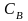, получим, например, в случае двусвязной области (по первой теореме Коши)

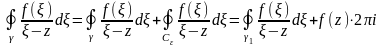
т.е. 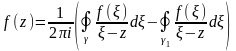. Обобщая доказанное на общий случай внутренних контуров, получим:

Теорема 2 Если функция аналитична в замкнутой области и внутренняя точка области, то равняется 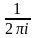, умноженному на сумму интегралов от 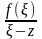по всем граничным контурам области, причем интеграл по внешнему контуру берется в направлении против часовой стрелки, а по внутренним контурам – по часовой стрелке.

Примеры

1 – не существует.

2 вычислим двумя способами (рисунок. 30)

Способ первый:

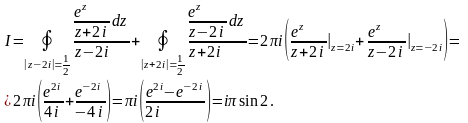
Способ второй: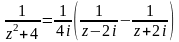 , поэтому

19 Функциональные ряды. Свойства равномерно сходящихся рядов

Рассмотрим функциональный ряд , членами которого являются функции комплексной переменной .В конкретной точке он превращается в числовой ряд, который может как сходиться, так и расходиться. Множество , в каждой точки которого сходится ряд, называется его областью сходимости. Обозначив в области частичную сумму ряда , а сумму – Получим следующее определение сходимости ряда в :

Определение 1 – сумма ряда в

Если при этом окажется, что номер зависит только от и не зависит от ,То такая сходимость называется равномерной на множестве .

Определение 2 Ряд сходится равномерно к на <=> ∀ >0 =>

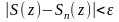
Замечание Формальная запись этих определений отличается только перестановкой мест выражений и , но это различие существенно.

В частности, для равномерно сходящихся функциональных рядов имеют место некоторые теоремы, аналогичные теоремам о конечных суммах функций. Причем, эти теоремы неверны для рядов, сходящихся неравномерно.

Как и для рядов в действительном области в комплексной области сохраняются (вместе с аналогичными доказательствами) следующие две теоремы:

Теорема 1 Если ряд, составленный из функций, непрерывных на множестве , равномерно сходится на этом множестве, то сумма ряда также непрерывна на . Кроме того, ряд можно почленно интегрировать по любой кусочно-гладкой кривой, содержащейся в .

Теорема 2 (признак Вейерштрасса равномерной сходимости). Если на множестве члены данного функционального ряда не превосходят по модулю соответствующих членов сходящегося положительного числового ряда (мажорантного ряда), то данный ряд сходится на абсолютно и равномерно.

Теорема 3 Пусть в области (любого вида)

1 функции 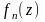являются аналитическими;

2

3 Ряд 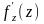равномерно сходится

4 не зависит от пути интегрирования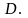

Тогда является аналитической в и = , т.е. ряд можно почленно дифференцировать.

Доказательство Обозначим .Тогда непрерывна в по теореме 1. Пусть и - любые точки из , фиксированная и переменная. Проинтегрируем это равенство по любому пути, соединяющему точки и :

= = = =

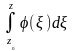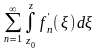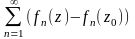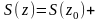
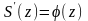
(параграф 16, теорема 4). Полученная формула показывает, что и интеграл не зависит от пути и, следовательно, является функцией от . Отсюда Поскольку производная правой части существует и равна (параграф 16, теорема 2), то существует и непрерывная в .

20 Степенные ряды. Теорема Абеля. Круг сходимости степенного ряда

Из всех функциональных рядов наибольший интерес представляют степенные ряды, т.е. ряды вида

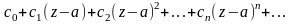
Теорема 1 (Абеля) Если ряд (1) сводится в точке , то он абсолютно сходится о любой точке , более близкой к , чем и равномерно сходится в любом замкнутом круг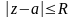е , где (cм. рисунок 31).

Доказательство Поскольку любую точку круга можно за счет выбора поместить в круг (где ), то достаточно доказать одновременно абсолютную (и равномерную) сходимость ряда в замкнутом круге. Для этого достаточно (параграф 19, теорема 2), подобрать в этом круге мажорантный числовой сходящийся ряд.

Т ак как по условию ряд сходится то (необходимое условие сходимости ряда). А всякая сходящаяся последовательность ограничена, т.е. 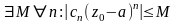.Далее,

Таким образом, в круге данный ряд мажорируется числовой геометрической прогрессией, которая сходится, так как её знаменатель по условию.

Следствие Если ряд (1) расходится в некоторой точке , то он подавно расходится в точках вне круга

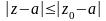
Следствие легко доказывается от противного. Теперь уже легко доказать теорему об области сходимости степенного ряда.

Теорема 2 Для всякого ряда 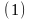существeт круг в котором он абсолютно сходится, а в любом круге наименьшего радиуса равномерно сходится. Вне круга ряд расходится. (В случае и 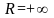круг сходимости соответственно вырождается в точку или охватывает всю плоскость).

Доказательство В точке любой ряд сходится. Проведём из неё любой луч (Рисунок 32). Логически возможны три случая: 1 На всём луче, кроме точки , ряд расходится. Тогда он будет расходится на всей плоскости, кроме точки (следствие теоремы 1), т.е. . 2 На всем луче ряд сходится. Тогда он будет абсолютно сходиться на всей плоскости и равномерно сходиться в любом замкнутом круге, т.е. . 3 Существует на луче точка , где ряд сходится, и точка 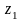, где ряд расходится. Разобьём отрезок 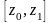пополам точкой 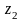и выберем тот из отрезков 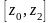или на одном конце которого ряд сходится, а на другом расходится. Его снова разобьём пополам и т.д. до бесконечности. По принципу Кантора существует точка , которая принадлежит всем отрезкам, которые мы делили пополам. В точках, лежащих на луче ближе к , чем , ряд абсолютно сходится, а в лежащих дальше расходится. Проведем теперь через точку окружность с центром в точке 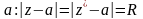. Тогда круг , и будет кругом сходимости, упомянутым в теореме. На границе круга поведение ряда может быть различным. называется радиусом сходимости ряда.

Пример Найдём круг сходимости ряда . Поскольку в круге сходимости степенной ряд абсолютно сходится, то достаточно исследовать ряд . К этому положительному ряду применим признак Даламбера 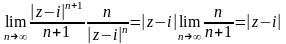. При ряд из модулей будет сходиться. Итак, кругом сходимости будет

21 Интегрирование и дифференцирование степенных рядов. Аналитичность суммы степенного ряда

Теорема 1 Пусть ряд

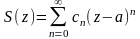
имеет радиус сходимости . Тогда:

1 степенные ряды, получающиеся из него почленным интегрированием или дифференцированием, имеют тот же радиус сходимости;

2 ряд можно почленно интегрировать по любой кусочно-гладкой кривой, содержащейся в круге сходимости;

S) сумма ряда имеет в круге сходимости производные любого порядка (следовательно, она аналитическая) и ряд можно почленно дифференцировать сколько угодно раз.

Доказательство 1 Пусть и соответственно радиусы сходимости рядов

и

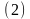
тогда для любых и

Отсюда следует, что если в некоторой точке абсолютно сходится ряд , то в ней абсолютно сходится ряд , а из последнего следует абсолютам сходимость ряда . Поэтому . Остается доказать, что 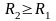, откуда и будет следовать . Иначе говоря, надо доказать, что из сходимости ряда в любой точке (т.е. 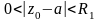) следует сходимость в ней ряда

Возьмём, 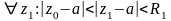а модуль общего члена ряда в точке умножим и разделим на

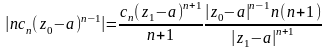
Тaк как ряд сходится в точке _, первый сомножитель справа стремится к нулю и, следовательно, ограничен, например, числом .Тогда для любого имеем:

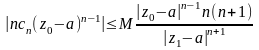
Таким образом, для ряда подобран мажорантный ряд, сходимость которого легко проверить по признаку Даламбера: .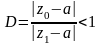

2 Если – любая кусочно-гладкая кривая в круге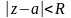 , то ее всегда можно поместить в круг меньшего радиуса , в котором ряд сходится равномерно. Поэтому по теореме параграфа 19 его можно почленно интегрировать по .

3 Достаточно воспользоваться теоремой 3 параграфа 19. Взяв любую точку из круга сходимости, можно затем так выбрать , чтобы и за область взять круг . Первые два условия теоремы 3 очевидны, третье условие следует из того, что круг сходимости ряда из производных совпадает с кругом сходимости данного ряда, а поэтому ряд равномерно сходится в круге .Наконец, четвертое условие следует из теоремы Коши параграфа.15

Поскольку полученный дифференцированием ряд снова является степенным, то многократно повторяя приведенное рассуждение, получим существование 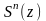для и возможность почленного дифференцирования ряда сколько угодно раз.

22 Разложение любой аналитической функции в ряд Тейлора. Бесконечная дифференцируемость аналитической функции

В предыдущем параграфе мы доказали, что сумма степенного рода является аналитической в круге его сходимости. Поставим обратную задачу: всякая ли аналитическая функция разлагается в степенной ряд?

Допустим сначала, что функция разлагается в ряд по степеням . Каковы его коэффициенты?

Пусть 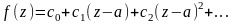для . Положив, получим Затем дифференцируя ряд параграфа 21 и снова положив , получим 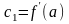. Повторяя этот процесс раз, будем иметь . Эти коэффициенты называются коэффициентами ряда Тейлора для функции , а соответствующий ряд – рядом Тейлора для этой функции. Итак, мы доказали теорему:

Теорема 1 Если функция является суммой степенного ряда в окрестности точки , то этот ряд единствен и является рядом Тейлора для данной функции.

Теорема 2 Если функция аналитическая в точке , то ее можно разложить вряд по степеням в круге , где - расстояние от точки до ближайшей к ней особой точки , т.е. точки, в которой нарушается аналитичность функции.

Доказательство Из условия очевидно, что в круге функция является аналитической. Любую точку этого круга можно поместить внутрь замкнутого круга 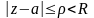(Рисунок 33), границу которого обозначим .

Тогда по формуле Коши 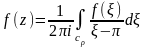Попытаемся подынтегральную функцию разложить по степеням:

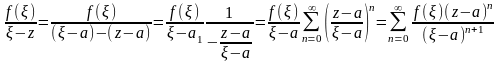
мы воспользовались формулой суммы геометрической прогрессии с учетом того, что ибо Для возможности почленного интегрирования полученного ряда воспользуемся теоремой 1 параграфа 19, для чего докажем равномерную сходимость ряда на окружности . Для 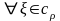имеем:

Правая часть неравенства – общий член числовой (не зависящей от переменной ) геометрической прогрессии, которая сходится, так как ее знаменатель, но модулю меньше 1. По теореме 2 параграфа 19 данный ряд равномерно сходится на и его можно почленно интегрировать:

где

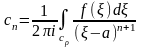
З амечание Если аналитическая в точке и имеет конечные особые точки вне окрестности , то ближайшая к особая точка всегда найдётся. Действительно, для достаточно большого в кольце 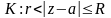особые точки, по условию, имеются. Из определения аналитичности функции в точке следует, что множество точек, в которых функция аналитическая, открыто, а множество особых точек всегда замкнуто. Тогда 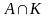— замкнуто и ограничено, т.е. является компактом. Функция непрерывна на , с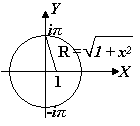 ледовательно и на . Поэтому на компакте она принимает н аим еньшее значение.

Теорема 2 представляет огромный практический интерес не только для ТАФ, но и для функций действительной переменной. Действительно, напомним, что задача разложения действительной функции в ряд Тейлора представляет значительную трудность. Даже бесконечная дифференцируемость функции в окрестности точки еще не обеспечивает ее разложимость в ряд Тейлора. Например, функция

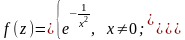
бесконечно дифференцируема на всей числовой прямой и 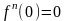для , т.е. сумма ее ряда Тейлора по степеням тождественно равна нулю, но не совпадает с .

Для аналитических же функций не только доказано их равенство сумме соответствующего ряда Тейлора, но и приведен простой способ отыскания области такого равенства.

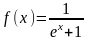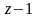Пример Пусть требуется функцию действительной переменной разложить в ряд по степеням . Для того, чтобы решить эту задачу на , решим ее сначала на множестве комплексных чисел. Для этого рассмотрим функцию на и найдем ее особые точки. Они будут корнями уравнения . Решим его: . Ближайшей к особой точкой будет (или ). Следовательно, функция разложима в ряд по степеням в круге (Рисунок 34). Значит, действительная функция разлагается в ряд по степеням . На интервале 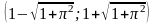. Найдя коэффициенты Тейлора получим:

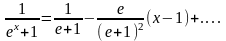
Интересно отметить, что не зная ТАФ, трудно было предполагать, что у данной функции радиус сходимости соответствующего ряда Тейлора выражается через число 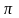,которое мы привыкли связывать с тригонометрическими функциями, а не с показательной.

Теорема 3 Если функция аналитически в точке , то она в некоторой окрестности этой точки имеет производные любого порядка (и все они, естественно, непрерывны).

Доказательство Согласно теореме 2, функция в некоторой окрестности точки разложима в ряд Тейлора. А по теореме 1 параграфа 21 сумма степенного ряда имеет в круге сходимости производные любого порядка.

Замечание Для функций действительной переменной существование непрерывной производной в окрестности точки еще не обеспечивает существование производных высших порядков. Например, функция 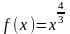имеет непрерывную производную на , но 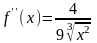не существует в точке .

Для соответствующей функции 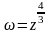точка является точкой ветвления, и, стало быть, в ней нарушается аналитичность.

Теорема 4 Если функция аналитическая в замкнутой односвязной области , ограниченной контуром , и — внутренняя точка области, то верна следующая интегральная формула Коши для производных:

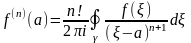
Доказательство Так как внутренняя точка , то она входит в вместе с некоторой своей окрестностью, границу которой обозначим (рисунок 35). В этой окрестности, по теореме 2, функция разлагается в ряд , где 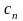определяются по формуле . С другой стороны, в силу единственности разложения (теорема 1), 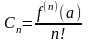, приравнивая эти значения , получим (с учетом того, что ).

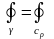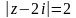Пример Вычислить интеграл .Поскольку аналитическая в круге , а точка лежит внутри него, то можно применить формулу Коши для :
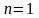