16 Первообразная аналитической функции. Формула Ньютона – Лейбница

Если функция аналитическая в односвязной области и фиксированная, а переменная точка этой области то интеграл 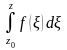по теореме 1 параграфа 15 не зависит от кривой интегрирования и, следовательно, является функцией от . Обозначим

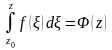
_{Теорема 1 При названных выше условиях} .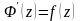

Доказательство Для любого 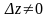найдем соответствующее приращение функции:

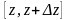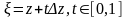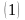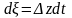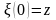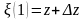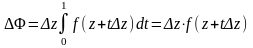В связи с независимостью интеграла от кривой можно считать его взятым по отрезку прямой . Формула параграф 11 позволяет свести его к определенному интегралу. Так как , , , то где 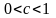. В последнем равенстве мы применим интегральную теорему о среднем. Деля полученное равенство на и переходя к пределу при 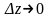, получим, в силу непрерывности в точке ,

Заметим, что аналитичность функции и неодносвязность в процессе доказательства понадобилась лишь дважды: 1 для установления независимости интеграла от пути интегрирования и 2 для непрерывности функции . Поэтому, не меняя основы приведенного доказательства, мы по сути дела получим более общую теорему, которая пригодится нам в будущем:

Теорема 2 Если функция непрерывна в произвольной области и если в этой области интеграл от функции не зависит от пути интегрирования, то функция

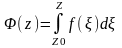является аналитической в и

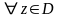
Определение Пусть – область. Если , то называется первообразной функции в .

Теорема 3 Все первообразные для данной непрерывной функции отличаются друг от друга на постоянную.

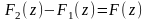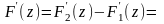
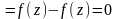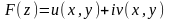Доказательство Пусть в области функция имеет две первообразные и . Обозначим . Очевидно, что и – функция аналитическая в . Кроме того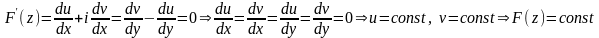 Теорема 4 (Формула Ньютона-Лейбница) Если 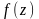непрерывна в и интеграл от нее не зависит от пути интегрирования (например, если аналитическая в односвязной области ), и – любая ее первообразная в области , то

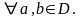
Доказательство Рассмотрим . Тогда:

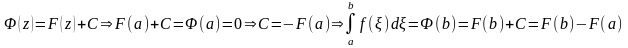
Пример

17 Интегральное представление логарифма

Рассмотрим интеграл , где любая точка, отличная от нуля. Аналитичность подынтегральной функции нарушается только в точке . Подсчитаем этот интеграл по любому пути, соединяющему точки и , но не пересекающему отрицательную полуось (Рисунок.25). Очевидно, что все пути можно поместить в односвязную область, не содержащую точку и, следовательно, интегралы по ним будут равны. В качестве наиболее удобного пути для подсчета интеграла выберем путь, изображенный на рисунок 26, где 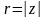, а путь из отрезка оси и дуги окружности. Если 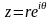, то уравнение дуги окружности имеет вид:

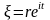
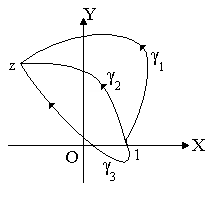
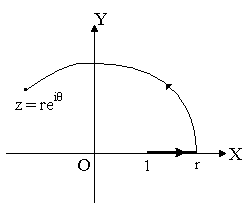
, где

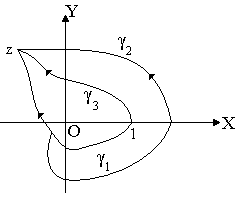
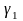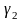Допустим теперь, что путь интегрирования пересекает отрицательную действительную полуось один раз (Рисунок 27), например или . Проведем , не пересекающую полуось . Тогда (см. пример 3 параграф 14)

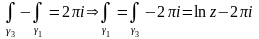
Если кривая пересекает отрицательную полуось раз, то очевидно, что

где означает количество пересечений отрицательной полуоси, понимаемое в алгебраическом смысле, т.е. с соответствующим знаком. Итак, рассматривая данный интеграл по всевозможным путям, мы получим все возможные значения многозначного логарифма .