34.)Основные постулаты квантовой механики

Квантовая механика – теория, устанавливающая описание, законы движения частиц и их систем, а также связь величин, характеризующих частицы и их системы, с физическими величинами.

1. Все физические величины могут изменяться непрерывно.

2. Все уравнения однозначно решаемы;

3. Аналитический метод исследования;

Соотношение неопределённостей: импульс-координата, энергия-время, фаза волны - число квантов.

Частица не может иметь одновременно и определенную координату (х, у, z), и определенную соответствующую проекцию импульса (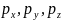 ), причем неопределенности этих величин удовлетворяют условиям:

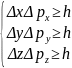
т. е. произведение неопределенностей координаты и соответствующей ей проекции импульса не может быть меньше величины порядка h.

 Нельзя со сколь угодной точностью одновременно измерить координату и импульс микрообъекта:

 

xph      (II.1)

Постулат №1.

 

Состояние частицы (или системы частиц) задано, если известна волновая функция (q)

Постулат №2.

 

Волновые функции подчиняются принципу суперпозиции: если в состоянии с волновой функцией ₁(q) некоторое измерение приводит к результату Х₁, а в состоянии ₂(q) - к результату Х₂, то всякая функция вида =с₁₁(q)+с₂₂(q)

описывает такое состояние, в котором измерение дает либо результат Х₁, либо Х₂.

 

Постулат №3.

 

Всякой физической величине L в квантовой механике сопоставлен линейный самосопряженный оператор. Единственно возможными величинами, которые может иметь эта физическая величина, являются собственные значения l операторного уравнения L=l

 

Постулат №4.

 

Возможная волновая функция состояния системы  получается при решении дифференциального уравнения ihd/dt=H, где H - оператор Гамильтона, а уравнение называется уравнением Шредингера.

 

Постулат №5.

 

Если произвести многократные измерения какой-либо динамической переменной l системы, находящейся в состоянии , то на основании результатов этих измерений можно определить ее среднюю величину. Эта средняя величина вычисляется по формуле:

l=^*Ldq/^*dq

35.)Волновая функция и уравнение Шредингера

Чтобы устранить трудности неодинакового распределением потоков микрочастиц, рассеянных или отраженных по различным направлениям,— в одних направлениях наблюдается большее число частиц, чем в других. , немецкий физик М. Борн (1882—1970) в 1926 г. предположил, что по волновому закону меняется не сама вероятность, а величина, названная амплитудой вероятности и обозначаемая ψ (х, у, z, t). Эту величину называют также волновой функцией (или ψ-функцией).

Физический смысл волновой функции заключается в том, что согласно копенгагенской интерпретации квантовой механики плотность вероятности нахождения частицы в данной точке пространства в данный момент времени считается равной квадрату абсолютного значения волновой функции этого состояния в координатном представлении.

Амплитуда вероятности может быть комплексной, и вероятность W пропорциональна квадрату ее модуля:W~| ψ (х, y, z, t)|² .(|ψ |²= ψ ψ *) ψ * —функция, комплексно сопряженная с ψ). Таким образом, описание состояния микрообъекта с помощью волновой функции имеет статистический, вероятностный характер: квадрат модуля волновой функции (квадрат модуля амплитуды волн де Бройля) определяет вероятность нахождения частицы в момент времени t в области с координатами х и х+dх, у и y+dy, z и z+dz.

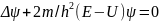(5)

Ур-е (5) называется ур-ем Шредингера для стационарных состояний. В это уравнение в качестве параметра входит полная энергия Е частицы. В теории дифференциальных уравнений доказывается, что подобные уравнения имеют бесчисленное множество решений, из которых посредством наложения граничных условий отбирают решения, имеющие физический смысл. Для уравнения Шредингера такими условиями являются условия регулярности волновых функций: волновые функции должны быть конечными, однозначными и непрерывными вместе со своими первыми производными. Таким образом, реальный физический смысл имеют только такие решения, которые выражаются регулярными функциями  Но регулярные решения имеют место не при любых значениях параметра Е, а лишь при определенном их наборе, характерном для данной задачи. Эти значения энергии называются собственными. Решения же, которые соответствуют собственным значениям энергии, называются собственными функциями. Собственные значения Е могут образовывать как непрерывный, так и дискретный ряд. В первом случае говорят о непрерывном, или сплошном, спектре, во втором — о дискретном спектре. Уравнение Шредингера — основное уравнение нерелятивистской квантовой механики, описывающее динамику частиц. Предложено Э. Шредингером в 1926 г. Состояние классической частицы в любой момент времени описывается заданием ее координат и импульсов (x,y,z,p_x,p_y,p_z). Зная эти величины в момент времени t, можно определить эволюцию системы под действием известных сил во все последующие моменты времени. Координаты и импульсы частиц сами являются величинами, непосредственно измеряемыми на опыте. В кван­то­вой физике состояние системы описывается волновой функцией ψ(x,y,z,t). Т. к. для квантовой частицы нельзя одновременно точно определить значения ее координат и импульса, то не имеет смысла говорить о движении частицы по определенной траектории, можно определить только вероятность нахождения частицы в данной точке в данный момент времени, которая определяется квадратом модуля волновой функции

W ~ |ψ(x,y,z,t)|².

    Эволюция квантовой системы в нерелятивистском случае описывается волновой функцией, удовлетворяющей уравнению Шредингера

где ψ(x,y,z,t) - волновая функция,   - оператор Гамильтона (оператор полной энергии системы).      В нерелятивистском случае

где m - масса частицы,   - оператор импульса,  (x,y,z,t) - оператор потенциальной энергии частицы. Задать закон движения частицы в квантовой механике это значит определить значение волновой функции в каждый момент времени в каждой точке пространства. Уравнение Шредингера играет в квантовой механике такую же роль, как и второй закон Ньютона в классической механике.     В стационарном состоянии

Ψ (x, y, z, t) = ψ(x, y, z)e^-iEt/ћ.

Так как вероятность найти частицу в момент t в точке x, y, z пропорциональна |Ψ(x, y, z, t )|² , то в данном случае она ~ |ψ (x, y, z)|², т.е. не зависит от времени. Аналогично, вероятность обнаружить значение физической величины, характеризующей систему, также не изменяется со временем, т.к. выражается через квадраты модулей волновых функций.     Уравнение Шредингера для стационарного состояния, когда потенцииальная энергия частицы явным образом не зависит от времени, имеет вид

ψ(x, y, z) = Eψ(x, y, z).

Это уравнение называют стационарным уравнением Шредингера.     Одна из специфических особенностей квантовых систем состоит в том, что энергетические спектры частиц, находящихся в ограниченном объеме пространства дискретны.