Диференціальні рівняння першого порядку з подільними змінними.

Розглянемо рівняння вигляду

, (8.5)

яке називається рівнянням з розділеними змінними. Дане рівняння є рівністю двох диференціалів деяких функцій, з чого випливає, що функції або рівні, або розрізняються на довільну сталу. Розв'язок рівняння одержимо, проінтегрувавши рівність

.

Рівняння з подільними змінними має вигляд

. (8.6)

Розділимо змінні, тобто перетворимо рівняння так, щоб біля диференціала стояла множником функція аргументу , а біля диференціала відповідно функція аргументу . Для цього поділимо рівняння на добуток функцій, що стоять біля “чужих” диференціалів , одержимо рівняння з розділеними змінними

.

Проінтегрувавши, прийдемо до розв'язку у вигляді

.

Рівняння є рівнянням з подільними змінними, тільки якщо , тоді замінивши на і, помноживши рівняння на , одержимо рівняння з розділеними змінними:

, , , , .

Рівнянням такого типу є рівняння . Знайдемо його загальний розв'язок, розділяючи змінні. Будемо мати

, , .

Запишемо довільну сталу у вигляді , що не змінить її змісту, тоді

.

Звідки – загальний розв'язок рівняння.

Розв’яжемо диференціальне рівняння

де шукана функція визначає чисельність населення. Нехай .

Розділимо змінні, одержимо . Проінтегрувавши, знайдемо, що , і, остаточно, – загальний розв'язок диференціального рівняння.

Обчислимо значення довільної сталої, виходячи з початкових умов.

Отже формула для визначення чисельності населення має такий вигляд:

де – численність населення в початковий момент часу; – коефіцієнт природного приросту; – число років.

Наприклад, якщо в деякий державі чисельність населення на даний момент часу 100 млн осіб, коефіцієнт природного приросту , то через 5 років чисельність населення цієї держави буде дорівнювати: млн осіб.

Приклад 8.1. Знайти частинний розв'язок диференціального рівняння , що задовольняє початковій умові .

Розв’язання. Дане рівняння є рівнянням з подільними змінними. Поділимо ліву і праву частину рівності на , одержимо:

, , , або . Звідки – інтеграл диференціального рівняння. Графіком інтеграла даного диференціального рівняння є сім’я кіл з центром у точці на вісі абсцис і радіусом . Надаючи різні значення, одержимо різні інтегральні криві сім’ї. Щоб знайти частинний розв'язок рівняння, підставимо значення у загальний розв'язок і обчислимо відповідне значення : Звідки , або . Отже, частинним розв'язком рівняння є функція .

Однорідні диференціальні рівняння першого порядку.

Будемо називати функцію однорідною -го порядку, якщо для неї справедлива тотожність

.

Наприклад, функція є однорідною другого порядку, тому що .

Диференціальне рівняння називається однорідним, якщо функція є однорідною нульового порядку.

Можна показати, що однорідна функція нульового порядку може бути зведена до функції вигляду .

Наприклад, ,

У такому випадку диференціальне рівняння набуває вигляду

(8.7)

Підстановкою рівняння можна звести до рівняння з подільними змінними. Дійсно, замість заданого рівняння (8.7) після підстановки одержимо рівняння або

Оскільки , то розділяємо змінні, і, інтегруючи, прийдемо до розв'язку .

Замінюючи в цьому розв'язку допоміжну функцію на приходимо до відповіді.

Приклад 8.2. Знайти загальний розв'язок диференціального рівняння

.

Розв’язання. Функція правої частини рівняння є однорідною нульового порядку, тому що

.

Розв’яжемо рівняння , ввівши заміну , Після підстановки в рівняння нової змінної, одержимо або – диференціальне рівняння з подільними змінними , де – шукана функція.

Після розділу змінних прийдемо до виразу .

Оскільки 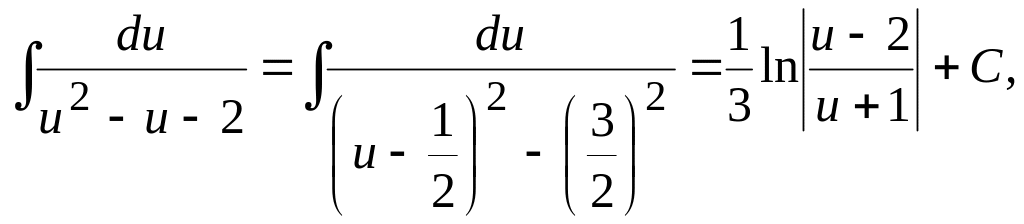то одержимо розв'язок у вигляді чи .

Оскільки , остаточний розв'язок приймає вигляд 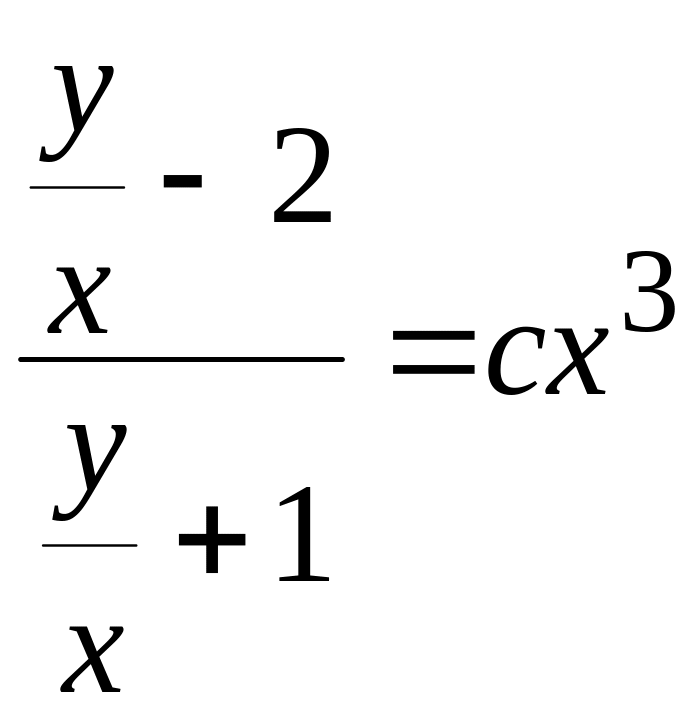або .

Диференціальне рівняння вигляду

(8.8)

буде однорідним, якщо і однорідні функції одного порядку.

Дійсно, розв’язуючи рівняння (8.8) відносно , одержимо

,

де – однорідна функція нульового порядку.

Приклад 8.3. Знайти частинний розв'язок диференціального рівняння , якщо .

Розв’язання. У даному рівнянні однорідні функції другого порядку. Розділимо рівняння на і розв'яжемо його відносно , одержимо

.

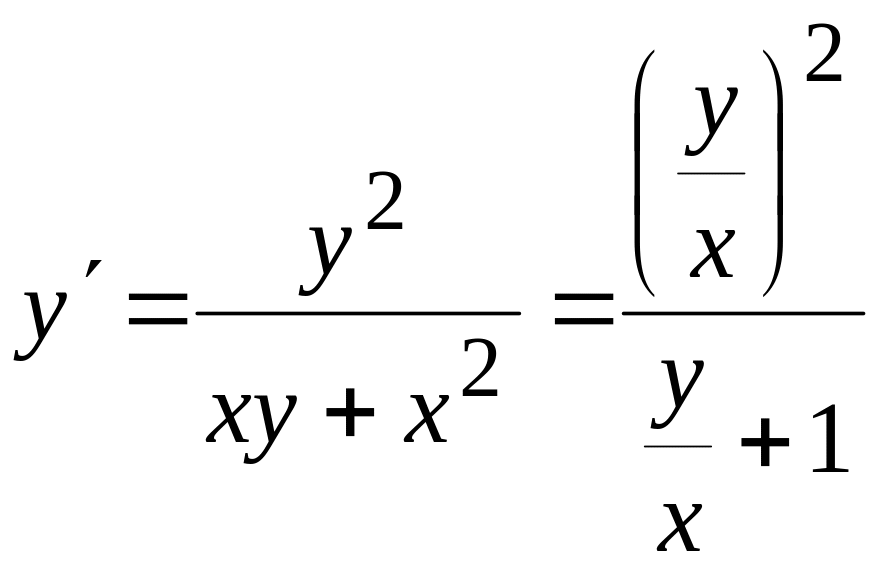Замінимо , отримаємо або .

Після поділу змінних прийдемо до рівняння . Звідки або .

Замінюючи , одержимо або – загальний інтеграл рівняння. Підставимо в загальний розв'язок початкові умови і знайдемо значення . Отже, частинний розв'язок заданого рівняння, що задовольняє початковій умові, має вигляд .