6. 6. Частинні похідні і диференціали вищих порядків

Якщо функція визначена в деякій області , то її частинні похідні у свою чергу будуть функціями багатьох змінних, визначеними в тій же області . Будемо називати їх частинними похідними першого порядку. Частинні похідні від частинних похідних першого порядку якщо вони існують, називають частинними похідними другого порядку від функції в цій точці і позначають, наприклад, у випадку функції двох змінних так:

; ;

; .

Так для функції ; , ; , , , .

Частинні похідні третього, четвертого і т.п. порядків вводяться аналогічно.

Частинна похідна будь-якого порядку, узята по різним змінним, наприклад, , , , і т.п. називається змішаною.

Очевидно, що для функції двох змінних можна визначити дві частинні похідні першого порядку, чотири частинні похідні другого порядку, вісім – третього і взагалі частинних похідних -го порядку.

Для функції одержуємо:

, , , , , , , і т.п.

Порівнюючи між собою значення змішаних похідних функції, бачимо, що ; ; , тобто змішані частинні похідні даної функції, що відрізняються лише послідовністю зроблених диференціювань, рівні між собою.

Означення 4.13. Значення диференціалу від першого диференціалу називається другим диференціалом і позначається .

Аналогічно можна ввести поняття диференціалу -го порядку як диференціалу від диференціалу -го порядку. Якщо змінні – незалежні, то:

;

.

Якщо аргументи є диференційованими функціями змінних , то

.

7. 7. Локальний екстремум функції багатьох змінних

Будемо говорити, що функція має в точці локальний максимум (мінімум), якщо знайдеться такий –окіл точки , в межах якого є найбільшим (найменшим) серед усіх значень цієї функції. Максимум і мінімум функції називають екстремумами функції.

Сформулюємо необхідну умову екстремуму.

Якщо функція має екстремум у точці , то частинні похідні першого порядку цієї функції обертаються в точці екстремуму в нуль, чи не існують.

Точки, в яких перші частинні похідні функції дорівнюють нулю чи не існують, називають критичними точками цієї функції.

Екстремум функції може бути лише в критичних точках, тобто якщо функція не має критичних точок, то вона не має екстремуму. З існування критичних точок ще не випливає існування екстремумів, тобто необхідна умова екстремуму не є достатньою.

Сформулюємо достатню умову екстремуму.

Якщо другий диференціал в критичній точці являє собою додатньо визначену квадратичну форму, то в критичній точці локальний мінімум. Якщо квадратична форма від’ємно визначена, то в критичній точці локальний максимум. Якщо квадратична форма знакозмінна, то в критичній точці локального екстремуму немає.

Зауважимо, що визначати вигляд квадратичної форми можна безпосередньо, а можна використовувати критерій Сильвестра.

Нехай ми маємо квадратичну форму відносно змінних , тобто многочлен другого степеня відносно змінних : , яка визначена своєю матрицею:

.

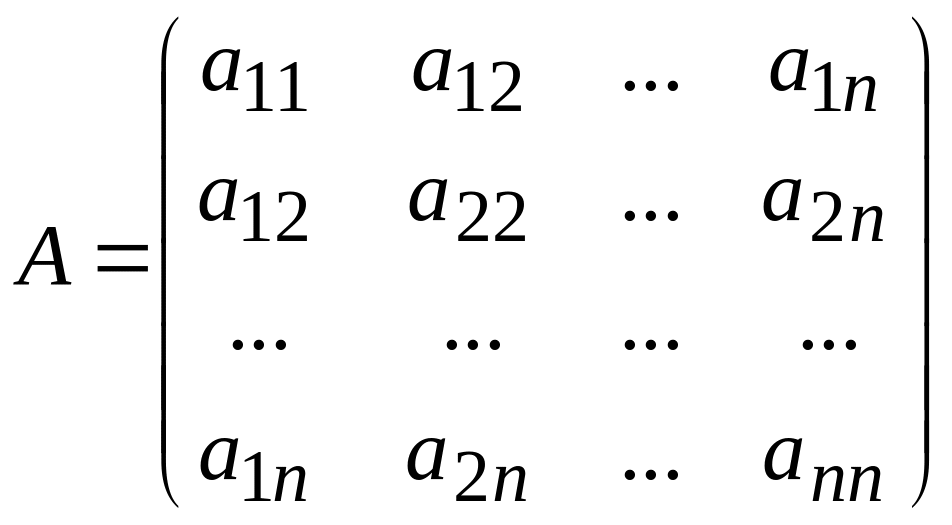Тоді в відповідності до критерію Сильвестра квадратичну форму вважають додатньо визначеною, якщо усі головні мінори матриці додатні.

Розглянемо випадок функції двох змінних. Обчислимо значення змішаних похідних другого порядку функції в критичній точці і позначимо , , .

Складемо вираз . Якщо в критичній точці , , то функція має екстремум у точці : мінімум при і максимум при . Якщо в критичній точці , то в точці екстремуму немає.

Якщо ж у критичній точці , то екстремум може бути, а може і не бути, потрібні додаткові дослідження.

Приклад 4.6. Дослідити на екстремум функцію .

Розв’язання. Для даної функції , . Знайдемо критичні точки функції, розв’язавши систему рівнянь

Одержимо три критичні точки: , , .

Обчислимо другі частинні похідні функції: , , .

Для точки , , . Тоді .

Достатня умова не дає відповіді на питання про існування екстремуму в точці . Дослідимо поведінку функції навколо точки. Наприклад, в околі точки на прямій функція набуває вигляду і є від'ємною. На прямій функція набуває вигляду і також є від'ємною. На прямій функція набуває вигляду і є додатною. Отже, в околі точки не виконується визначення ні мінімуму, ні максимуму, отже, в точці екстремуму немає.

Для точки , , , отже, екстремум є. Оскільки , то це мінімум: .

Аналогічно переконуємося в тому, що в точці функція також має мінімум: .