Невласні інтеграли від необмежених функцій.

Нехай функція неперервна на проміжку і необмежена поблизу .

Тоді для будь-якого 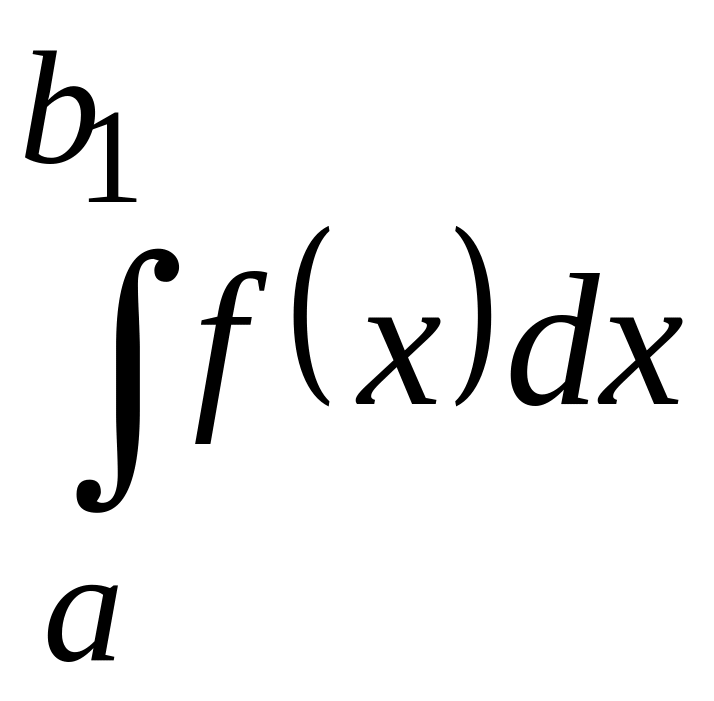існує і

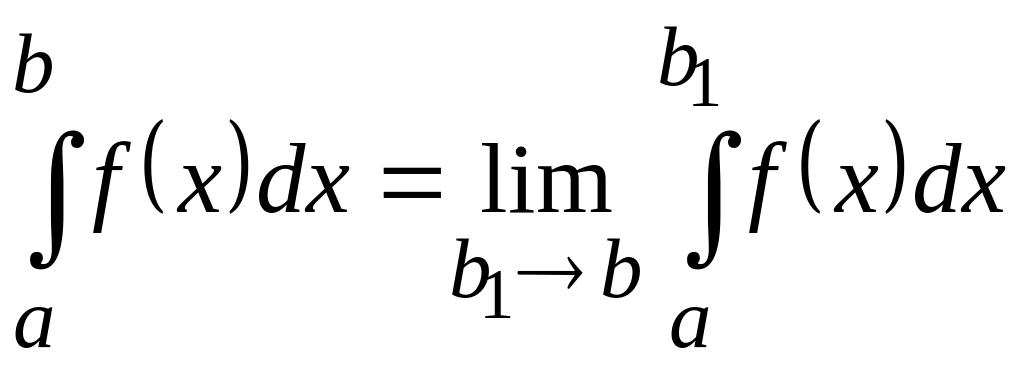. (5.37)

Цей інтеграл може бути як збіжним, так і розбіжним, усе залежить від поведінки первісної при .

Приклад 5.35. Обчислити інтеграл .

Розв’язання. Підінтегральна функція визначена для всіх , у точці функція розривна і є необмеженою. Застосовуючи формулу (5.37), одержимо

Даний інтеграл збіжний.

Рис. 5.5.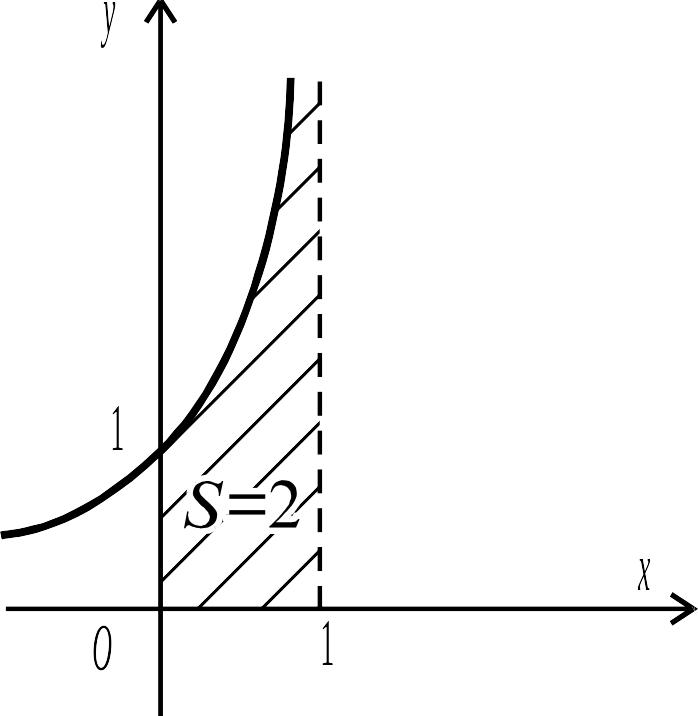

Геометричний зміст такого інтеграла для невід’ємної : площа нескінченної смуги, обмеженої знизу відрізком вісі , ліворуч і праворуч прямими , , зверху – кривою .

На рис. 5.5 показано геометричний зміст інтеграла

.

Аналогічно, можна ввести інтеграл

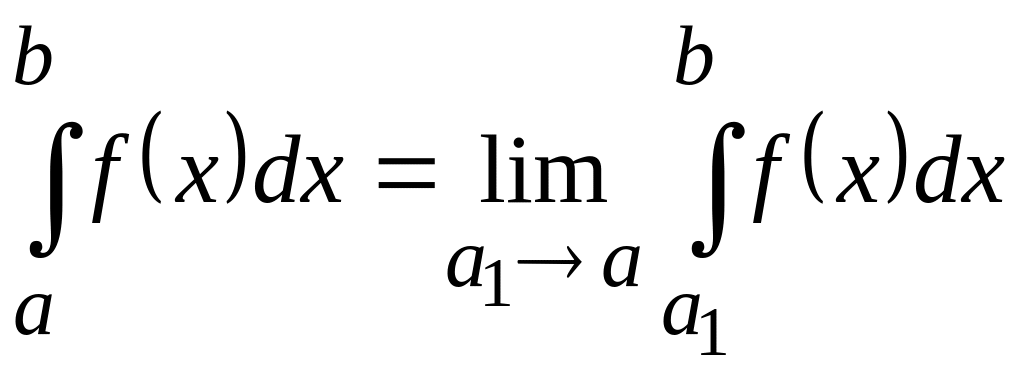, де . (5.38)

Якщо підінтегральна функція всередині відрізка має розрив у деякій точці , то

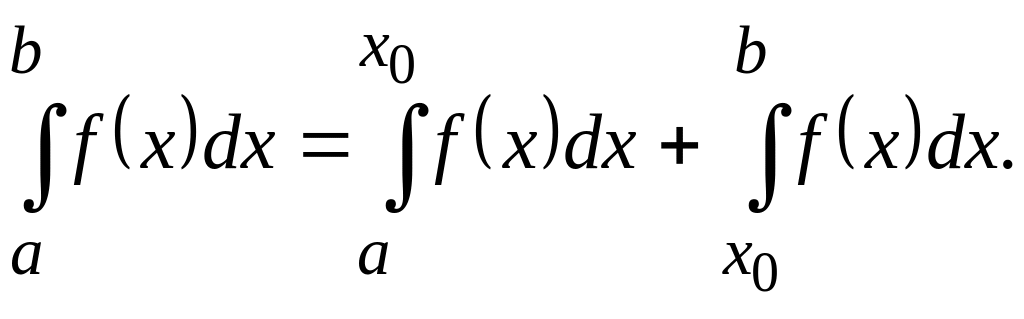
Приклад 5.36. Обчислити інтеграл .

Розв’язання. Підінтегральна функція розривна у точці . Тому .

Внаслідок парності підінтегральної функції , одержимо .

Отже, даний інтеграл розбіжний. Як і для невласних інтегралів з нескінченними межами, для кожного з невласних інтегралів від необмежених функцій є справедливою узагальнена формула Ньютона–Лейбніца.

25. 13. Наближене обчислення визначених інтегралів

Відомо, що не для всякої неперервної функції її первісна виражається через елементарні функції. У цих випадках обчислення визначених інтегралів за формулою Ньютона–Лейбніца неможливе, незважаючи на те, що визначений інтеграл функцій існує, і застосовуються наближені методи, які ґрунтуються на геометричному змісті інтеграла.

Спосіб прямокутників.

Як відомо, визначений інтеграл для невід’ємної функції є площею криволінійної трапеції (рис. 5.6).

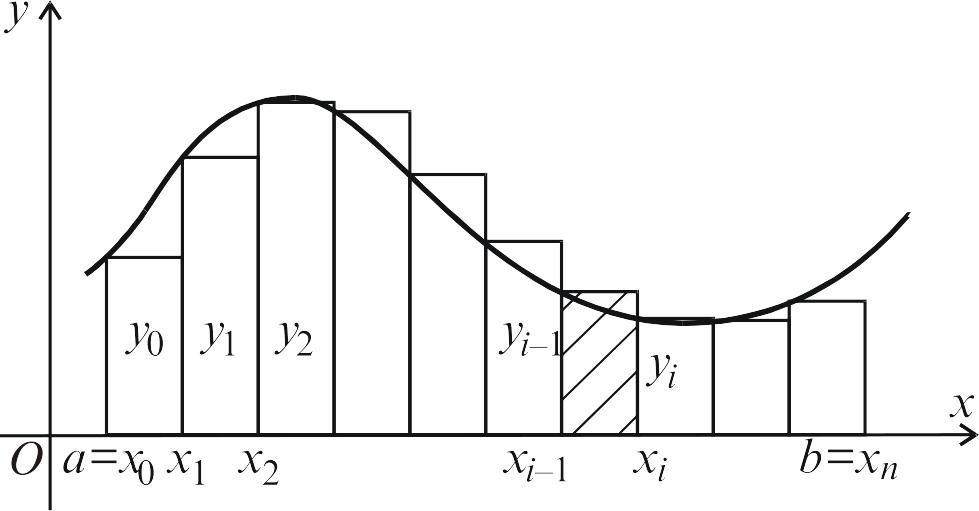
Рис. 5.6

Розіб'ємо відрізок на рівних частин, довжини одержаних відрізків будуть рівні .

Внаслідок побудови криволінійна трапеція розбилася на вертикальних смуг однакової ширини , площу кожної з яких обчислимо наближено як площу прямокутника з основою і висотою, що дорівнює значенню функції в лівому кінці основи

.

Тоді або

. (5.39)

Якщо прийняти за висоту кожного прямокутника значення функції в правому кінці основи, одержимо

. (5.40)

Формули (5.39) і (5.40) називають формулами прямокутників. У випадку, якщо формули (5.39) і (5.40) геометрично означають заміну площі криволінійної трапеції площею східчастої фігури, складеної з прямокутників. Очевидно, що похибка, отримана при обчисленні інтеграла за формулами прямокутників буде тим меншою, чим більше число .

Доведено, якщо похідна підінтегральної функції існує й обмежена на відрізку , то оцінка результату може бути виконана за формулою

, (5.41)

де – найбільше значення модуля першої похідної на відрізку .

Спосіб трапецій.

Спосіб трапеції відрізняється від способу прямокутників тим, що площа кожної смуги обчислюється приблизно як площа трапеції з основами і та висотою :

.

Тоді або

. (5.42)

Геометрично обчислення інтеграла від невід’ємної функції за формулою трапецій зводиться до заміни площі відповідної криволінійної трапеції площею, складеної з прямокутних трапецій (рис. 5.7).

Очевидно, що обчислення інтеграла за формулою трапецій дає більш точний результат, ніж за формулою прямокутників.

Якщо існує й обмежена на відрізку друга похідна підінтегральної функції , то оцінка результату може бути отримана за формулою

, (5.43)

де – найбільше значення модуля на відрізку .

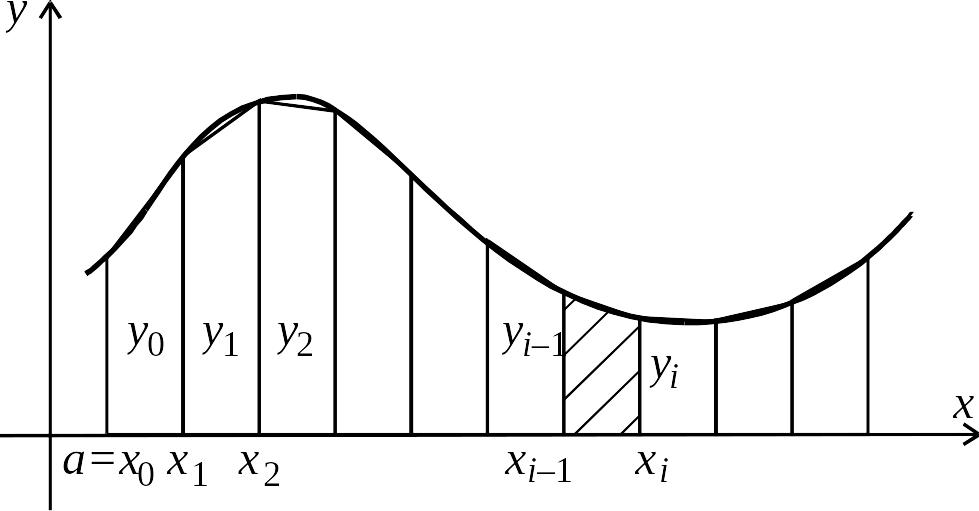
Рис. 5.7.