3. 3. Частинні похідні функції

Нехай у деякій області задана функція . У деякій точці , що належить області , її значення . Дамо аргументу приріст , не змінюючи інші змінні. Функція одержить приріст

,

який називається частинним приростом функції по змінній .

Означення 4.9. Частинною похідною по від функції в точці називається границя відношення частинного приросту функції за аргументом до приросту аргументу за умови, що приріст аргументу прямує до нуля, тобто

.

Позначається частинна похідна по так: , , , .

З означення частинних похідних випливає, що частинна похідна по будь-якій змінній є звичайною похідною цієї функції по обраній змінній, за умови, що інші змінні є сталими.

Тому обчислення частинних похідних не вимагає нових формул і правил диференціювання, крім тих, які відомі з диференціального числення функції однієї змінної.

Наприклад, для функції частинні похідні мають вигляд:

; .

4. 4. Повний диференціал

Розглянемо неперервну функцію . Дамо аргументам приріст. При цьому функція також одержить приріст, який назвемо повним приростом функції:

, або

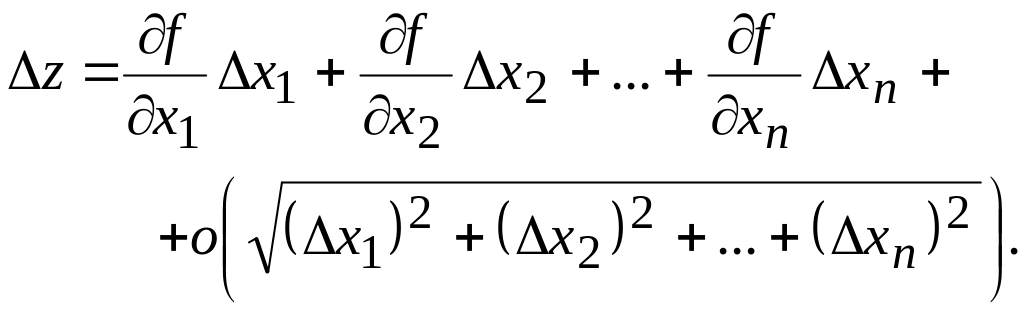
Означення 4.10. Повним диференціалом функції двох змінних називається головна частина її приросту і позначається

. (4.4)

Диференціал незалежної змінної дорівнює її приросту, тобто . Тоді

. (4.5)

Можна стверджувати, що

. (4.6)

Цю формулу застосовують у наближених обчисленнях, заміняючи приріст функції її диференціалом.

Приклад 4.2. Обчислити наближено .

Розв’язання. Для функції , , ; ; ; ; . Тоді:

.

Підставляючи значення, одержуємо

.

На підставі формули (4.6) у наближених обчисленнях оцінюють похибки обчислень.

Приклад 4.3. При вимірі циліндра були отримані результати: , . З якою абсолютною і відносною похибками може бути обчислений об'єм?

Розв’язання. Об'єм циліндра обчислюється за формулою . За умовою задачі , . Отже, похибки змінних: , . Знайдемо частинні похідні й і їхні значення при , :

.

Обчислюємо максимальну абсолютну похибку:

.

Відносну похибку результату, :

.

5. 5. Похідна функції за даним напрямком. Градієнт

Нехай – функція, визначена в області . Нехай точка належить області . Розглянемо деякий напрямок , заданий напрямними косинусами кутів, утворених цим напрямком з осями координат. При переміщенні в напрямку точки в точку функція одержить приріст, що називається приростом функції в даному напрямку.

Означення 4.11. Похідною функції за напрямком називається границя відношення приросту функції в цьому напрямку до величини переміщення за умови, що останнє прямує до нуля:

.

В двовимірному випадку маємо:

. (4.7)

Похідна є швидкість зміни функції в заданому напрямку.

Приклад 4.4 Знайти похідну функції в точці за напрямком, що йде від цієї точки до точки .

Розв’язання. Пряма , за напрямком якої потрібно знайти похідну, має напрямний вектор . Знайдемо напрямні косинуси: ; .

Знайдемо частинні похідні заданої функції й обчислимо їх у точці : , , , . Скориставшись формулою (4.7), одержимо: .

Нехай функція диференційована в деякій області і точка належить цій області.

Означення 4.12. Градієнтом функції в точці називається вектор, координатами якого є частинні похідні функції, обчислені в точці .

Градієнт функції позначають символом . Таким чином,

. (4.8)

Використовуючи градієнт функції, похідну за напрямком можна записати у вигляді

, (4.9)

де – одиничний вектор заданого напрямку, координати якого дорівнюють відповідно напрямним косинусам.

Оскільки , де – кут між векторами і , то з формули (4.9) випливає, що похідна за напрямком набуває найбільше значення, якщо вектор має той же напрямок, що і .

Оскільки є швидкістю зміни функції в напрямку , то градієнт цієї функції спрямований в бік найбільшої зміни функції, а довжина цього вектора дорівнює найбільшій швидкості зміни функції.

Можна показати, що спрямовано по нормалі до лінії рівня , що проходить через точку .

Приклад 4.5. Знайти градієнт функції і показати, що він спрямований по нормалі до ліній рівня даної функції.

Розв’язання. Знаходячи частинні похідні, одержимо

.

Кутовий коефіцієнт градієнта . Лінії рівня даної функції задаються рівнянням . Обчислимо кутовий коефіцієнт дотичної до лінії рівня як , для цього знайдемо похідну функції . Продиференціюємо останню рівність, за умови, що – аргумент, а – функція, одержимо , звідки , тобто кутовий коефіцієнт дотичної до лінії рівня дорівнює . Таким чином, , тобто градієнт функції спрямований по нормалі до лінії рівня.