22. 10. Заміна змінної у визначеному інтегралі

Нехай потрібно обчислити визначений інтеграл , де функція неперервна на відрізку . При цьому диференційована функція на відрізку , причому , . Покажемо, що

. (5.33)

Дійсно, за формулою Ньютона–Лейбніца

,

де – деяка первісна для функції на відрізку . Оскільки при цьому функція є первісною для функції на відрізку , то

.

Враховуючи, що , , одержуємо , тобто формула (5.33) вірна.

Приклад 5.30. Обчислити інтеграл .

Розв’язання. Замінимо , . Якщо змінюється від 0 до 1, то змінна змінюється від 0 до . Застосовуючи формулу (5.33) одержуємо

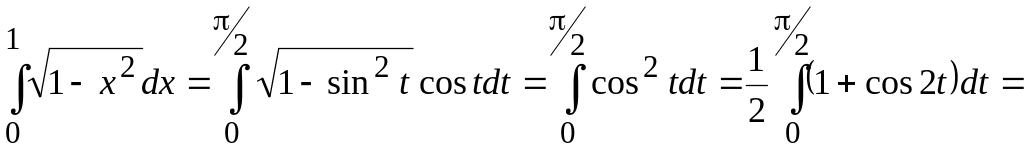
Зауваження. Варто звернути увагу на те, що при обчисленні визначеного інтеграла за допомогою заміни змінної немає необхідності повертатися до колишньої змінної.

23. 11. Інтегрування частинами у визначеному інтегралі

Нехай функції і неперервні на відрізку і мають на цьому відрізку неперервні похідні. Тоді диференціал їхнього добутку дорівнює: .

Проінтегрувавши рівність на відрізку , одержимо

.

Оскільки , то формула набуває вигляду , звідки

. (5.34)

Приклад 5.31. Обчислити інтеграл .

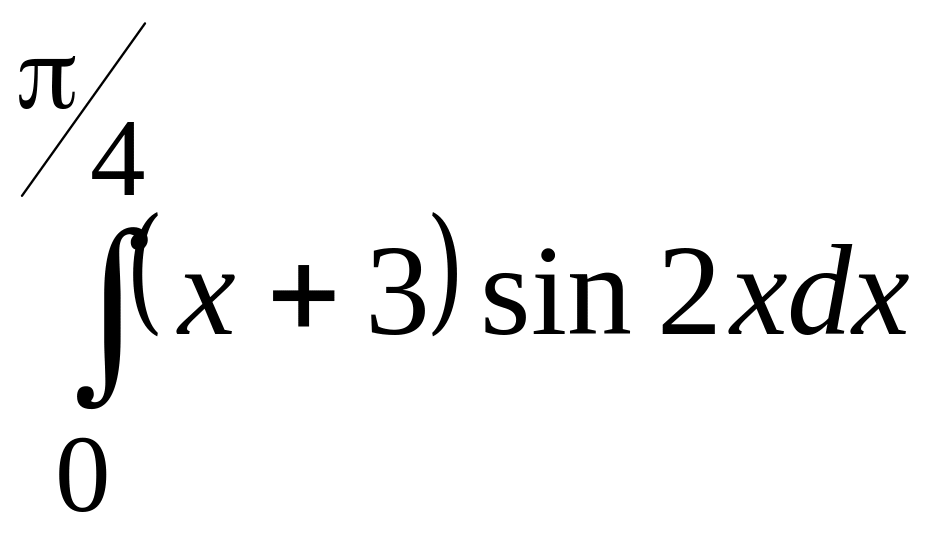Розв’язання. Нехай , . Тоді , . Застосовуючи формулу (5.34), одержимо

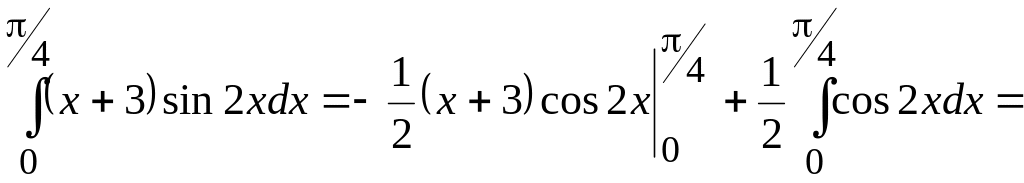
24. 12. Невласні інтеграли

Вводячи визначений інтеграл як границю інтегральної суми, припускали, що відрізок інтегрування скінченний, а підінтегральна функція на ньому неперервна.

Якщо хоча б одна з цих умов не виконується, дане визначення втрачає зміст, а визначений інтеграл називається невласним.

Невласні інтеграли з нескінченними границями інтегрування.

Нехай функція неперервна на проміжку . Тоді вона є неперервною на будь-якому відрізку , що належить проміжку й існує її визначений інтеграл

.

При цей інтеграл є функцією своєї верхньої границі і тоді

. (5.35)

Якщо така границя існує і скінченна, інтеграл називається збіжним; якщо ж границя нескінченна чи не існує, то він розбіжний.

Приклад 5.32. Обчислити інтеграл .

Розв’язання. Згідно (5.35) маємо

Рис. 5.4.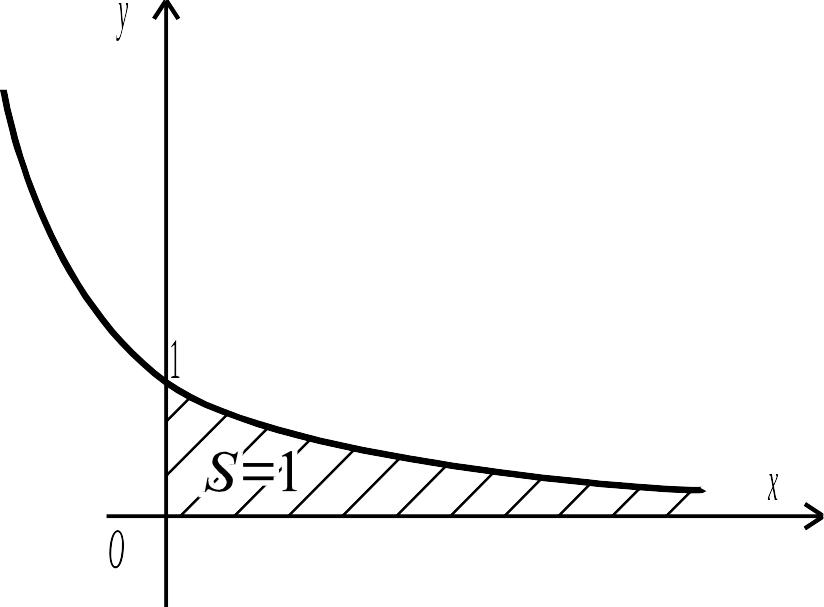

тобто інтеграл збігається. Як бачимо, результат залежить від поведінки первісної функції при . Геометричний зміст такого інтеграла – для невід’ємної дорівнює площі смуги, що необмежена праворуч. На рис. 5.4 показано геометричний зміст інтеграла .

Приклад 5.33. Обчислити інтеграл .

Розв’язання. Застосовуючи формулу (4.14), одержуємо

тобто інтеграл розбіжний.

Аналогічно, якщо функція неперервна на , то

, (5.36)

може бути як збіжним, так і розбіжним.

Приклад 5.34. Обчислити інтеграл .

Розв’язання. За означенням

інтеграл збіжний.

Очевидно, що результат залежить від поведінки первісної при .

Для функції , неперервної на всій числовій осі, невласний інтеграл визначається рівністю де – будь-яке число. Якщо хоча б один з інтегралів правої частини рівності розбіжний, інтеграл теж розбіжний.

Невласні інтеграли мають властивості, аналогічні властивостям визначених інтегралів.

Зокрема, якщо ввести умовні позначки то одержимо для розглянутих інтегралів узагальнення формули Ньютона–Лейбніца:

;

;

.