Розділ 4. Диференціальне числення функції багатьох змінних

1. 1. Основні поняття

У багатьох практичних задачах доводиться користатися величинами, що залежать не від однієї незалежної змінної, а від декількох змінних.

Означення 4.1. – вимірним координатним простором називається множина усіляких впорядкованих сукупностей , де . Кожну таку сукупність будемо називати точкою – вимірного координатного простору, тобто , де – координати точки .

Означення 4.2. Координатний простір називається – вимірним евклідовим простором , якщо між двома будь-якими точками та визначена відстань:

.

Означення 4.3. Нехай кожному числу ставиться в відповідність точка , тоді ряд точок , , ..., , ..., називається послідовністю точок . Послідовність точок позначають .

Означення 4.4. Якщо кожній точці з множини точок ставиться в відповідність за певним законом деяке число , то кажуть, що на множині задано функцію або . При цьому множину називають областю задання функції.

Той факт, що змінна є функцією змінних записують у вигляді

(4.1)

для явного завдання функції, і

(4.2)

для неявного завдання функції.

Приклад 4.1. Знайти область визначення функцій:

а) ; б) .

Розв’язання. Для випадку а) функція визначена для всіх значень , , при яких дріб існує. Очевидно, що це ті і , при яких . Отже, область визначення даної функції зображується точками площини , що не належать прямій (рис.4.1).

Для випадку б) функція визначена при або . Графічно область визначення даної функції зображується точками круга (рис.4.2).

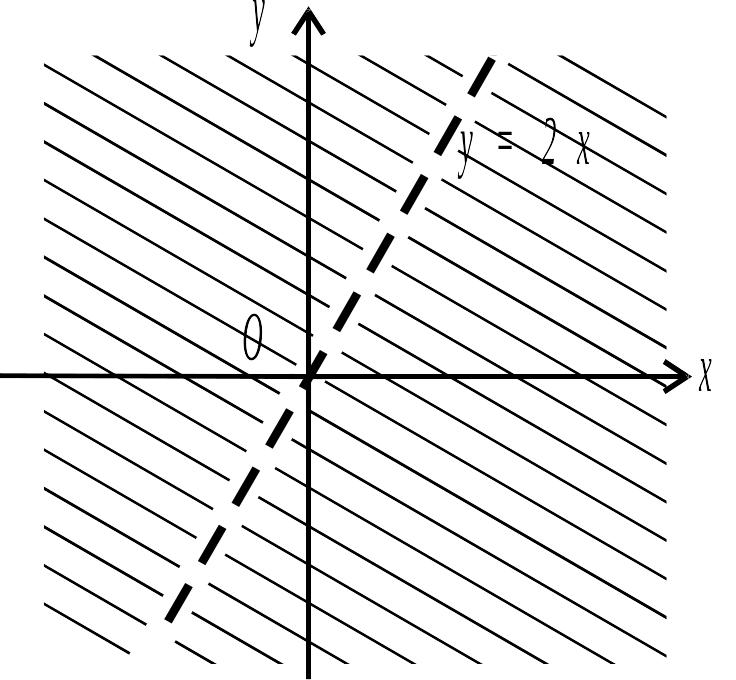
Рис. 4.1.	Рис. 4.2.

Означення 4.5. Лінією рівня функції називається множина усіх точок, в яких функція набуває стале значення.

Рівняння лінії рівня має вигляд

, . (4.3)

Надаючи в цьому рівнянні різні значення сталої , будемо одержувати різні лінії рівня.

Для функції лініями рівня є концентричні кола , (рис.4.3). При коло вироджується в точку.

Для функції лініями рівня будуть прямі , (рис.4.4).

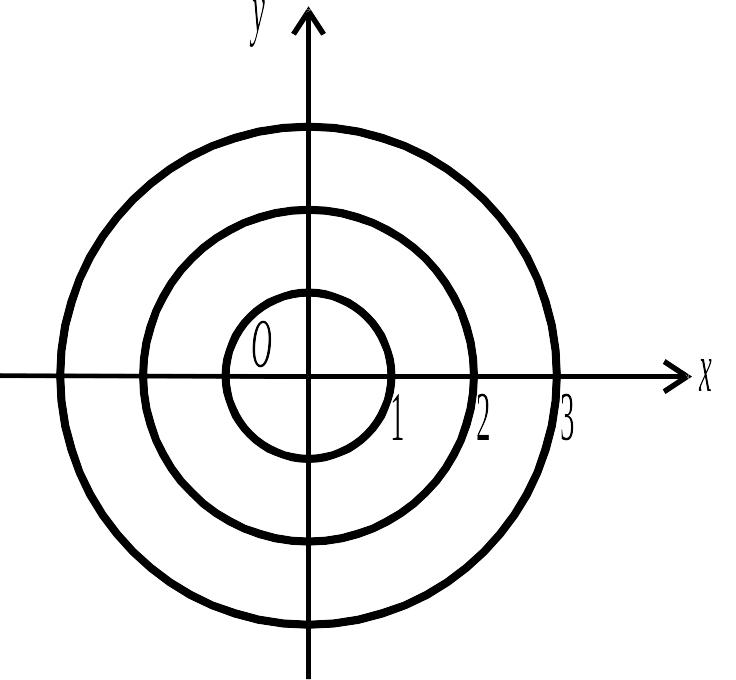
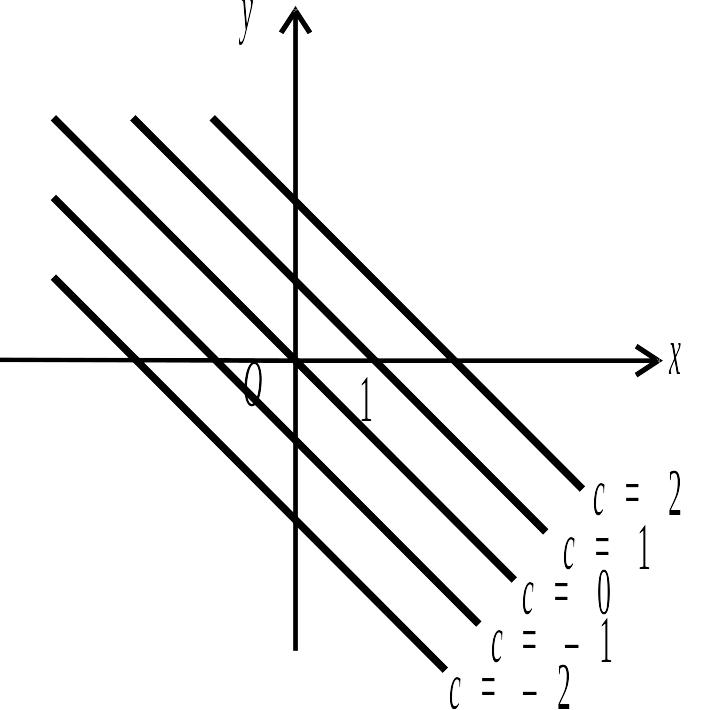
Рис. 4.3.	Рис. 4.4.

Лінії рівня використовуються при складанні географічних карт (лінії рівня – лінії, в яких висота точок земної поверхні над рівнем моря однакова), при складанні метеорологічних карт (лінії рівня – ізобари, ізотерми, ізохори) і т.д.

2. 2. Границя і неперервність

Для визначення границі функції введемо поняття околу точки .

Означення 4.6. –околом точки будемо називати множину точок, віддалених від точки на відстань, що менше числа , тобто .

Означення 4.7. Число називається границею функції при , якщо для кожного, як завгодно малого, наперед заданого додатного числа знайдеться такий -окіл точки , що для будь-якої точки з цього околу виконується нерівність .

Позначають або .

Усі теореми про границі, доведені для функції однієї змінної поширюються і на функції багатьох змінних.

Наприклад, , .

Зауважимо, що слід розрізняти –кратні границі і повторні границі, тобто

і .

Означення 4.8. Функція називається неперервною в точці , якщо виконується рівність , тобто значення неперервної функції в точці і її границя при збігаються.

На випадок функції багатьох змінних переносять властивості неперервних функцій однієї змінної: сума, різниця, добуток неперервних у точці функцій неперервні; частка двох неперервних у точці функцій неперервна, якщо .

Аналогічно узагальнюється властивість неперервності складної функції.

Функція , неперервна в кожній точці деякої області , називається неперервною в цій області.

При вивченні функції однієї змінної розглядалися основні властивості функцій, неперервних на відрізку. Ці властивості можна узагальнити на випадок функції багатьох змінних.

До основних властивостей функції, неперервної в замкнутій обмеженій області , віднесемо такі властивості.

1. Функція обмежена в області .

2. Функція досягає свого найменшого і найбільшого значень.

3. Функція набуває хоча б в одній точці області будь-яке значення, що лежить між і .