- •Розділ 1. Теорія множин
- •1. Поняття множини
- •2. Найпростіші операції над множинами
- •3. Числові множини
- •4. Обмежені множини. Верхні та нижні грані множин
- •5. Поняття функції (відображення)
- •6. Еквівалентні множини. Потужність множин
- •7. Потужність континуума
- •Розділ 2. Послідовності. Функції однієї змінної
- •1. Числові послідовності
- •2. Границя послідовності
- •3. Застосування послідовностей в економіці
- •4. Поняття функції
- •5. Способи задання функції
- •6. Деякі властивості функцій
- •7. Функція, обернена до даної
- •8. Класифікація функцій
- •9. Основні методи побудови графіків функцій
- •10. Приклади застосування функцій в економіці
- •11. Границя функції
- •12. Нескінченно малі і нескінченно великі функції
- •13. Основні теореми про границі функцій
- •14. Обчислення границь функцій
- •15. Істотні границі Перша істотна границя
- •Друга істотна границя
- •16. Порівняння нескінченно малих
- •17. Неперервність функції в точці
- •18. Властивості функцій, неперервних в точці
- •19. Точки розриву і їхня класифікація
- •20. Властивості функцій, неперервних на відрізку
14. Обчислення границь функцій
На підставі теорем про границі, а також властивостей нескінченно малих і нескінченно великих функцій можна зробити наступний висновок: щоб обчислити границю функції при , необхідно у функцію підставити замість його граничне значення і обчислити результат.
Наприклад,
 .
.
Оформляють
запис так:
![]() .
.
При
обчисленні границі функції
![]() при
при
![]() в знаменнику дробу одержуємо нуль, тоді
результат обчислень беруть у квадратні
дужки, підкреслюючи символіку записів;
тут нуль є символом нескінченно малої.
Записують так:
в знаменнику дробу одержуємо нуль, тоді
результат обчислень беруть у квадратні
дужки, підкреслюючи символіку записів;
тут нуль є символом нескінченно малої.
Записують так:
![]() .
.
Якщо ж
у результаті підстановки замість
його граничного значення
виходять так звані невизначеності
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
для обчислення границі приходиться
проводити перетворення функції, говорять,
“звільнятися від невизначеності”.
,
для обчислення границі приходиться
проводити перетворення функції, говорять,
“звільнятися від невизначеності”.
Зокрема,
якщо невизначеність
отримана при обчисленні границі
дробово-раціональної чи дробово-ірраціональної
функції при
,
необхідно в чисельнику і знаменнику
дробу виділити нескінченно малу
![]() і скоротити на неї. Відзначимо, що ділення
чисельника і знаменника дробу на
нескінченно малу функцію можливо,
оскільки це не нуль, а реальна величина,
що змінюється так, що її значення можуть
бути як завгодно малими.
і скоротити на неї. Відзначимо, що ділення
чисельника і знаменника дробу на
нескінченно малу функцію можливо,
оскільки це не нуль, а реальна величина,
що змінюється так, що її значення можуть
бути як завгодно малими.
Приклад
2.7.
Обчислити
![]() .
.
Розв’язання.
Безпосередня підстановка у функцію
граничного значення аргументу приводить
до невизначеності вигляду
.
Вирази чисельника і знаменника містять
у собі нескінченно малу
![]() :
:
![]() ,
,
![]() .
.
Тому
![]() .
.
Приклад
2.8.
Обчислити
![]() .
.
Розв’язання.
Тут
безпосередня підстановка у функцію
![]() приводить до невизначеності
.
Щоб виділити в чисельнику нескінченно
малу при
приводить до невизначеності
.
Щоб виділити в чисельнику нескінченно
малу при
![]()
![]() помножимо чисельник і знаменник дробу
на вираз, спряжений чисельнику (позбудемося
від ірраціональності в чисельнику):
помножимо чисельник і знаменник дробу
на вираз, спряжений чисельнику (позбудемося
від ірраціональності в чисельнику):
![]() .
.
Тоді
![]()
![]() .
.
Розповсюджена границя відношення многочленів при прямуванні аргументу до нескінченності, що дає невизначеність :


Тут
 .
.
Наприклад,
![]() ,
,
![]() і т.д.
і т.д.
Невизначеності
![]() і
і
![]() приводять до невизначеностей
або
,
перетворивши досліджувану функцію у
дріб.
приводять до невизначеностей
або
,
перетворивши досліджувану функцію у
дріб.
Приклад
2.9.
Обчислити
![]() .
.
Розв’язання. Безпосередньою підстановкою замість граничного значення одержимо невизначеність .
Перетворимо
досліджувану функцію, помноживши і
розділивши її на суму
![]() ,
одержимо
,
одержимо
![]() .
.
Тоді
![]()

15. Істотні границі Перша істотна границя
Розглянемо
границю
![]() .
Функція
.
Функція
![]() парна,
парна,
![]() .
За умовою
,
тому досить розглянути значення x,
що задовольняють нерівності
.
За умовою
,
тому досить розглянути значення x,
що задовольняють нерівності
![]() .
.
Візьмемо
дугу кола радіуса
і кут, радіанна міра якого дорівнює
(рис. 2.31). На рис. 2.31:
![]()
Рис. 2.31.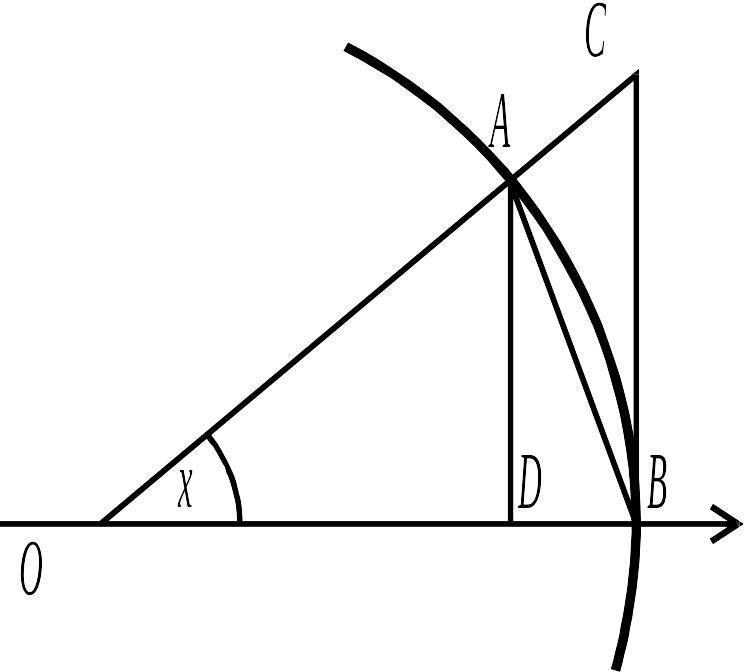
![]() ,
сектора
і трикутника
,
сектора
і трикутника
![]() ,
що відповідно дорівнюють
,
що відповідно дорівнюють
![]() ,
,
![]() ,
,
![]() або
або
![]() ,
,
,
,
![]() .
Очевидно
.
Очевидно
![]() ,
звідки
,
звідки
![]() .
Розділимо останні нерівності на
.
Розділимо останні нерівності на
![]() і одержимо
і одержимо
![]() ,
,
![]() .
.
Функція
розташована між функціями
![]() і
і
![]() ,
причому
,
причому
![]() ,
тому за теоремою 2.5 одержимо
,
тому за теоремою 2.5 одержимо
![]() . (2.5)
. (2.5)
Границя (2.5) називається першою істотною границею. Використовуючи першу істотну границю можна показати, що
![]() . (2.6)
. (2.6)
Дійсно,
![]() ,
,
і також
![]() . (2.7)
. (2.7)
Замінимо
![]() ,
звідки
,
звідки
![]() ,
причому при
,
,
причому при
,
![]() .
Одержимо
.
Одержимо
 .
.
Аналогічно,
![]() . (2.8)
. (2.8)
Границі 2.5–2.8 допомагають розкрити невизначеність у випадку, якщо під знаком границі тригонометричні функції.
Приклад
2.10.
Обчислити
![]() .
.
Розв’язання.
Безпосередньою підстановкою замість
граничного значення одержуємо
невизначеність
.
Перетворимо даний дріб, застосувавши
формулу
![]() ,
одержимо
,
одержимо