100. 12. Нескінченно малі і нескінченно великі функції

Означення 2.9. Функція називається нескінченно малою при ( – число або один із символів , , ), якщо для кожного, як завгодно малого наперед заданого додатнього числа можна вказати таке додатне число , що для всіх , які задовольняють нерівність , виконується умова . Тобто, функція є нескінченно малою при , якщо .

Наприклад, , при є нескінченно малою, її значення можуть бути менше будь-якого наперед заданого числа, а при її значення прагнуть до числа 9, у чому легко переконатися підстановкою у функцію окремих частинних значень.

Означення 2.10. Функція називається нескінченно великою при ( – число або один із символів , , ), якщо .

Наприклад, функція при може приймати як завгодно великі значення, отже, у зазначених умовах вона є нескінченно великою.

Нескінченно малі і нескінченно великі функції мають такі властивості.

Властивість 1. Алгебраїчна сума скінченного числа нескінченно малих при функцій є функцією нескінченно малою.

Нехай і – нескінченно малі при функції.

Це значить, що для кожного, як завгодно малого, наперед заданого додатного числа знайдуться такі додатні і , що при , виконається умова , а при виконається умова . Виберемо менше з чисел і ( ) і оцінимо :

.

А це значить, що функція нескінченно мала при .

Властивість 2. Добуток обмеженої функції на нескінченно малу при є функція нескінченно мала.

Нехай функція обмежена, тобто знайдеться таке додатне число , що , а функція – нескінченно мала при : яке б як завгодно мале не взяли, знайдеться таке додатне число , що для усіх виконається умова . Оцінимо , що і потрібно було довести.

Наприклад, при добуток є функцією нескінченно малою, оскільки функція , обмежена.

Наслідок 1. Добуток сталої на нескінченно малу функцію є функція нескінченно мала.

Наслідок 2. Добуток скінченного числа нескінченно малих при функцій є функцією нескінченно малою.

Дійсно, нескінченно мала при функція в околі точки є обмеженою.

Властивість 3. Сума нескінченно великих при функцій є функцією нескінченно великою.

Відзначимо, що для різниці ця властивість невірна.

Властивість 4. Добуток обмеженої функції на нескінченно велику при є функцією нескінченно великою при . Наприклад, функція є нескінченно великою при , оскільки функція обмежена.

Наслідок. Добуток сталої на нескінченно велику при функцію є функцією нескінченно великою при .

Властивість 5. Функція, обернена за величиною до нескінченно великої при є нескінченно малою при , і навпаки.

Якщо прийняти символом нескінченно малої функції 0, символом нескінченно великої , то усі викладені властивості можна записати так:

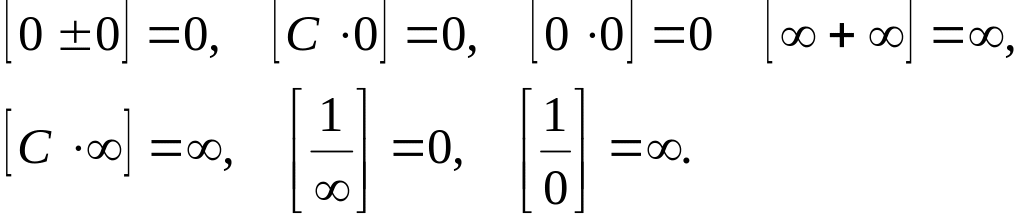
Квадратні дужки вказують на символіку представлених записів.

101. 13. Основні теореми про границі функцій

Теорема 2.2. Якщо число є границею функції при , то справедлива рівність , де при – нескінченно мала функція.

Дійсно, якщо , виходить, що для кожного, як завгодно малого, наперед заданого додатного числа можна вказати таке додатне число що для всіх , що задовольняють нерівність , виконується умова , тобто функція є нескінченно малою при . Назвемо її . Маємо , звідки .

Легко довести і зворотне твердження: якщо функція представлена у вигляді суми сталої і нескінченно малої при функції, то ця постійна є границею функції при .

Теорема 2.3. Якщо функція має границю при , то вона єдина.

Припустимо, що при функція має дві границі і , причому . Але тоді в силу теореми 2.2 і , де , – нескінченно малі при функції. Віднімемо отримані рівності: або . Це можливо тільки при , оскільки при .

Теорема 2.4. Якщо , , то:

а) ;

б) ;

в) 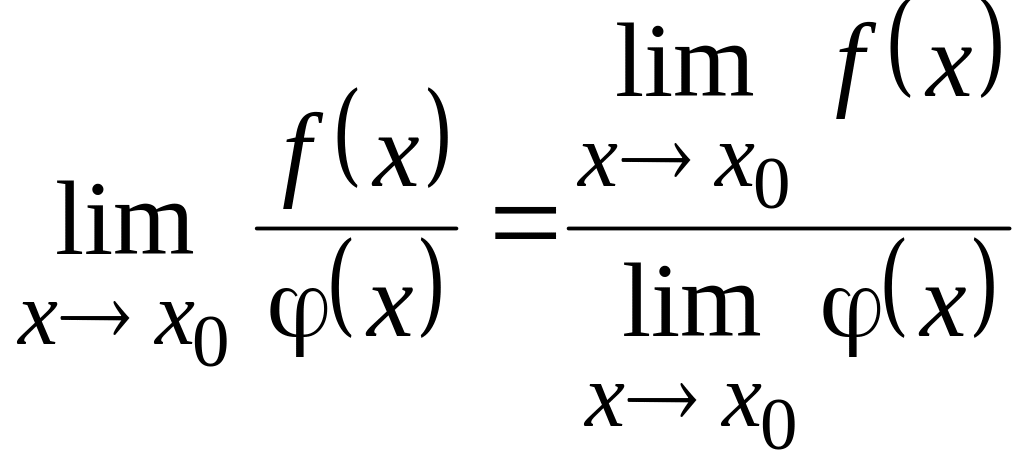, якщо .

Сформулювати теорему можна так.

Якщо дві функції мають границі при , то границя їхньої алгебраїчної суми дорівнює алгебраїчній сумі границь цих функцій, границя добутку дорівнює добутку границь, границя частки дорівнює частці границь заданих функцій, за умови, що границя знаменника не дорівнює нулю при .

Доведемо теорему для випадку “а”.

Дійсно, оскільки , , то на підставі теореми 2.2. і , де , – нескінченно малі при .

Але тоді , де – стала, – нескінченно мала при функція. Отже, відповідно до теореми 2.2 число є границею функції , або

.

Що і потрібно було довести.

Аналогічно доводиться теорема для випадку “б”.

Для випадку “в” дріб представимо у вигляді

,

де функція є нескінченно малою при .

Тому .

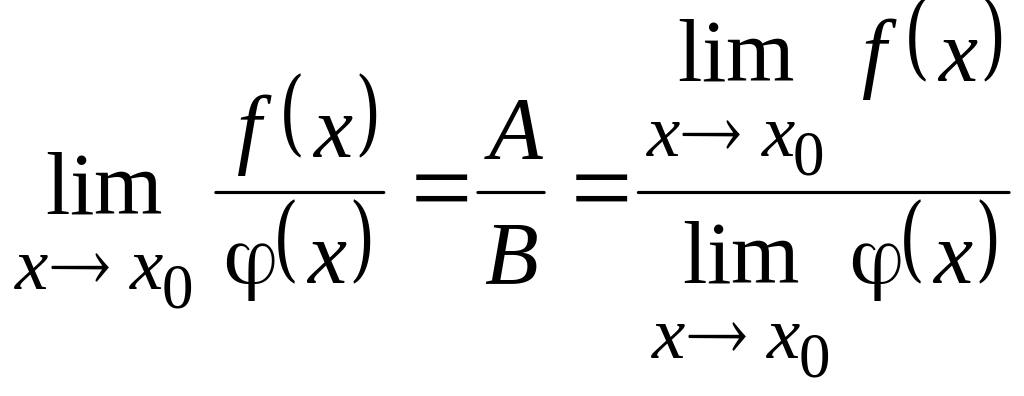Наслідок. Сталі множники можна виносити за знак границі, тобто

.

Теорема 2.5. Якщо в околі точки виконуються нерівності і , то і .

Для доведення розглянемо – довільну, що збігається до , послідовність значень аргументу функцій і .

Відповідні послідовності і значень цих функцій мають границю, рівну , тобто , при .

Використовуючи нерівності, дані в умовах теореми, можна записати

.

Звідси , значить, .

Зауваження. Усі теореми про границі вірні також і у випадку, якщо є одним із символів , , .