Вопрос 24. Институты как фундаментальные детерминанты агрегирования индивидуальных предпочтений. Теорема о медианном избирателе.

Теорема о медианном избирателе:

Если в одномерном пространстве выбора предпочтения всех избирателей имеют только одну точку максимума, медианный избиратель (чья точка оптимального выбора – x_m) никогда не окажется в проигрыше, если коллективные решения принимаются по правилу простого большинства.

• Предпосылки:

1. x^*_i – точка идеального выбора i-того избирателя в пространстве «полезность – общественное благо», если, и только если U_i(x^*_i)>U_i(x) для всех x≠x^*_i.

2. Пусть y и z – две точки на оси х, расположенные с одной стороны от точки x^*_i, y,z≥ x^*_i или y,z≤ x^*_i, тогда предпочтения избирателя имеют только одну точку максимума, если, и только если [U_i(y)> U_i(z)]↔[|y-x^*_i|<|z-x^*_i|]. Чем ближе точка на оси x к точке идеального выбора i-того избирателя, тем она предпочтительнее для него.

3. Пусть {x^*₁, x^*₂, …, x^*_n} – точки идеального выбора сообщества, состоящего из n индивидов. N_R – это число x^*_i≥x_m, а N_L – это число x^*_i≤x_m, x_m – оптимальный выбор медианного избирателя если, и только если N_R≥n/2, N_L≥n/2.

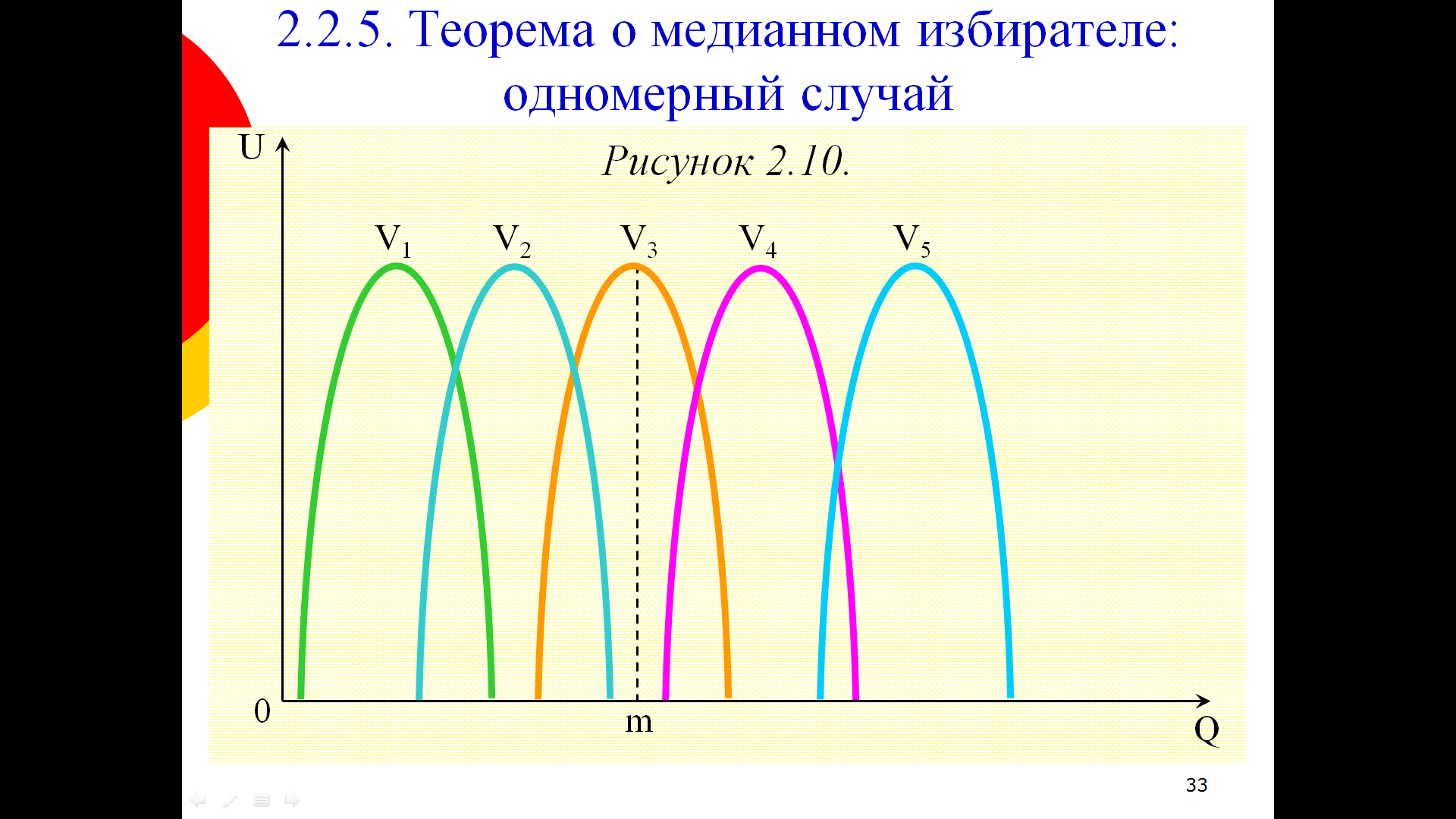
• Доказательство:

• Возьмем некую точку z≠x_m, например, пусть z<x_m. Пусть R_m – число точек идеального выбора, расположенных справа от x_m.

• По определению одновершинности предпочтений, для всех избирателей, чьи точки идеального выбора принадлежат множеству R_m, x_m предпочтительнее z.

• По определению позиции медианного избирателя, R_m≥n/2.

• Поэтому, число избирателей, для которых x_m предпочтительнее z по крайней мере R_m≥n/2.

• Поэтому медианный избиратель не может проиграть.

• Аналогично доказывается, что позиция медианного избирателя не может уступить любой позиции z>x_m.