
- •Кафедра общей и технической физики
- •ДИФРАКЦИЯ ЭЛЕКТРОНОВ
- •Методические указания к лабораторным работам
- •САНКТ-ПЕТЕРБУРГ
- •Научный редактор доц. Ю.И. Кузьмин
- •ВВЕДЕНИЕ
- •Кафедра общей и технической физики
- •ИЗУЧЕНИЕ ОСОБЕННОСТЕЙ ЭФФЕКТА ХОЛЛА
- •Методические указания к лабораторной работе
- •САНКТ-ПЕТЕРБУРГ
- •Научный редактор доц. Т.В. Стоянова
- •ВВЕДЕНИЕ
- •СОДЕРЖАНИЕ ОТЧЁТА
- •Кафедра общей и технической физики
- •ЯВЛЕНИЯ ПЕРЕНОСА И ЭЛЕМЕНТЫ КВАНТОВОЙ СТАТИСТИКИ
- •Методические указания к лабораторным работам
- •САНКТ-ПЕТЕРБУРГ
- •Научный редактор доц. Т.В. Стоянова
- •Кафедра общей и технической физики
- •Опыт Франка – Герца
- •Методические указания к лабораторным работам
- •САНКТ-ПЕТЕРБУРГ
- •Научный редактор доц. Т.В. Стоянова
- •ВВЕДЕНИЕ
- •Кафедра общей и технической физики
- •Р-N-ПЕРЕХОД И ЕГО ПРИМЕНЕНИЕ
- •Методические указания к лабораторным работам
- •САНКТ-ПЕТЕРБУРГ
- •ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
- •Работа 8. Исследование температурных характеристик диодов
- •ВЛИЯНИЕ ТЕМПЕРАТУРЫ НА ПРОБИВНОЕ НАПРЯЖЕНИЕ ДИОДА
- •ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА
- •ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
- •ОБРАБОТКА РЕЗУЛЬТАТОВ
- •ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ И ПРОВЕРКИ ВЛАДЕНИЯ МАТЕРИАЛОМ
- •ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ ОТЧЁТА
- •СОДЕРЖАНИЕ
- •Кафедра общей и технической физики
- •СОЛНЕЧНЫЕ ЭЛЕМЕНТЫ
- •Методические указания к лабораторным работам
- •САНКТ-ПЕТЕРБУРГ
- •Научный редактор доц. Т.В. Стоянова
- •ВВЕДЕНИЕ
- •Национальный минерально-сырьевой университет «Горный»
- •Кафедра общей и технической физики
- •САНКТ-ПЕТЕРБУРГ
- •Теоретические основы лабораторной работы
- •Описание установки
- •Порядок выполнения
- •Контрольные вопросы
- •Кафедра общей и технической физики
- •ОПРЕДЕЛЕНИЕ ШИРИНЫ ЗАПРЕЩЁННОЙ ЗОНЫ ГЕРМАНИЯ
- •Методические указания к лабораторным работам
- •САНКТ-ПЕТЕРБУРГ
- •Научный редактор доц. Н.А. Тупицкая
- •ВВЕДЕНИЕ
- •1.5 Примесная проводимость
- •общая физика
- •ФИЗИКА ТВЕРДОГО ТЕЛА
- •Основные теоретические сведения
- •Выполнение работы
- •Работа 6. Гальваномагнитные явления в твердых телах
- •Порядок проведения работы
- •Содержание отчета
- •СОДЕРЖАНИЕ
- •Примесные полупроводники
- •Акцепторные полупроводники.
- •Металлы
- •3.3. Контакт металл-полупроводник
- •а полная концентрация дырок в валентной зоне p, соответственно, равна
- •Электропроводность кристалла
- •Примеры решения задач
- •12. Контактные явления
- •Примеры решения задач
- •К-серия
- •8. Спектры молекул
- •Жесткость молекулы
- •Характерную частоту вращательного движения можно оценить как
- •а полная концентрация дырок в валентной зоне p, соответственно, равна
- •Электропроводность кристалла
- •Примеры решения задач
- •12. Контактные явления
- •15. Элементы дозиметрии излучений
- •Константы двухатомных молекул

vk.com/club152685050 | vk.com/id446425943
18.Определите, какая энергия требуется для полного отрыва электрона от однократно ионизированного атома гелия, если электрон находится в основном состоянии.
19.Фотон с энергией 15 эВ выбивает электрон из атома водорода, находящегося в основном состоянии. С какой скоростью движется электрон вдали от ядра?
20.Определить для иона He+ потенциал ионизации, первый потенциал возбуждения и длину
волны основной линии серии Лаймана.
21.Определить работу, которую необходимо совершить, чтобы удалить электрон со второй боровской орбиты атома водорода за пределы притяжения его ядром.
22.Первый потенциал возбуждения атома водорода φ1 = 10,2 эВ. При какой температуре Т средняя
кинетическая энергия атомов водорода равна энергии возбуждения?
23.Определить электрона на 2-й круговой боровской орбите иона He+.
24.Определите, какая энергия требуется для полного отрыва электрона от однократно ионизированного атома гелия, если электрон находится в состоянии с n = 3.
25.Определите частоту света, излучаемого атомом водорода при переходе электрона на уровень
n = 2, если радиус орбиты электрона изменился в 9 раз.
2. ВОЛНЫ ДЕ БРОЙЛЯ
Де Бройль сопоставил свободной частице, имеющей импульс p, монохроматическую волну с
длиной волны
h p 2 p . |
(2.1) |
Примеры решения задач
1. Найти длину волны де Бройля пули массой 9 г, летящей со скоростью 100 м/с.
Решение. Длина волны де Бройля определяется по формуле λ = h/p = h/mV. Подставляя численные значения, получим λ = 7,36 10–32 м.
2. Кинетическая энергия протона в четыре раза меньше его энергии покоя. Вычислить
дебройлевскую длину волны протона.
Решение. Длина волны де Бройля λ определяется по формуле λ = h/p, где p – импульс частицы. Так как по условию задачи Ек = E0/4, то кинетическая энергия Ек протона сравнима с его энергией покоя
Е0. В этом случае импульс р и кинетическая энергия Ek связаны релятивистским |
соотношением |
||
p 1 c |
|
, где с – скорость света в вакууме. Отсюда найдем p = 3E0/4c. |
Учитывая это, |
Ek Ek 2E0 |
|||
получим дину волны λ = 4hc/(3E0) = 1,77∙10-15 м. |
|
||
7
vk.com/club152685050 | vk.com/id446425943
Задачи для самостоятельного решения
1. При какой скорости электрона его дебройлевская длина волны будет равна а) 500 нм; б)
0,1 нм?
2.Какой кинетической энергией должен обладать электрон, чтобы дебройлевская длина волны была равна его комптоновской длине волны?
3.Чему должна быть равна кинетическая энергия протона, чтобы дебройлевская длина волны совпадала с его комптоновской длиной волны?
4.При каком значении скорости дебройлевская длина волны частицы равна ее комптоновской длине волны?
5.Кинетическая энергия электрона в три раза меньше его энергии покоя. Чему равна дебройлевская длина волны электрона?
6.Масса движущегося электрона в два раза больше его массы покоя. Вычислить дебройлевскую длину волны электрона.
7.Чему равна дебройлевская длина волны протона, движущегося со скоростью 0,6с (с – скорость
света в вакууме)?
8.Вычислить дебройлевскую длину волны электрона, прошедшего ускоряющую разность потенциалов 511 кВ.
9.Вычислить дебройлевскую длину волны протона, прошедшего ускоряющую разность потенциалов 120 кВ.
10.Чему равна дебройлевская длина волны теплового нейтрона, обладающего энергией, равной средней энергии теплового движения при температуре 300 К?
11.Средняя кинетическая энергия электрона в невозбужденном атоме водорода, равна 13,6 эВ. Вычислить дебройлевскую длину волны электрона.
12.Кинетическая энергия нейтрона равна его энергии покоя. Определить дебройлевскую длину волны нейтрона.
13.Найти дебройлевскую длину волны молекул водорода, соответствующую их наиболее вероятной скорости при комнатной температуре.
14.Найти дебройлевскую длину волны молекул СО2, соответствующую их средней скорости при
комнатной температуре.
15.Найти дебройлевскую длину волны молекул азота, соответствующую их наиболее вероятной скорости при температуре 77 К.
16.Найти дебройлевскую длину волны молекул кислорода, соответствующую их средней скорости при температуре –70 ºС.
17.Найти дебройлевскую длину волны молекул воды, соответствующую их средней скорости при комнатной температуре.
8

vk.com/club152685050 | vk.com/id446425943
18. Вычислить |
дебройлевскую длину волны электрона, |
|
|
|
|
|
|
||
имеющего кинетическую энергию 100 эВ. |
|
|
|
|
19. Вычислить |
дебройлевскую длину волны протона, |
E |
||
|
|
U |
||
имеющего кинетическую энергию 200 эВ. |
|
|
||
|
|
|
||
20. Вычислить |
дебройлевскую длину волны атома урана, |
|
|
|
|
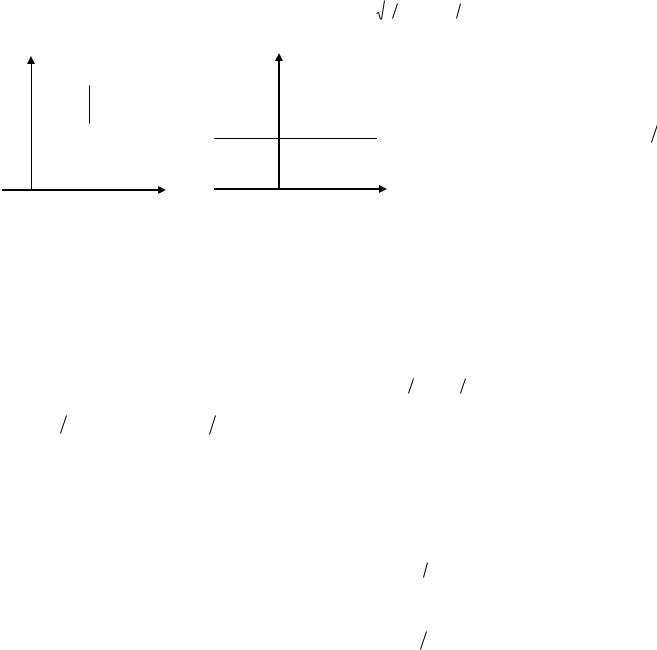
Рис.2.1 |
|||
имеющего кинетическую энергию 100 эВ. |
|
|||
|
|
|
||
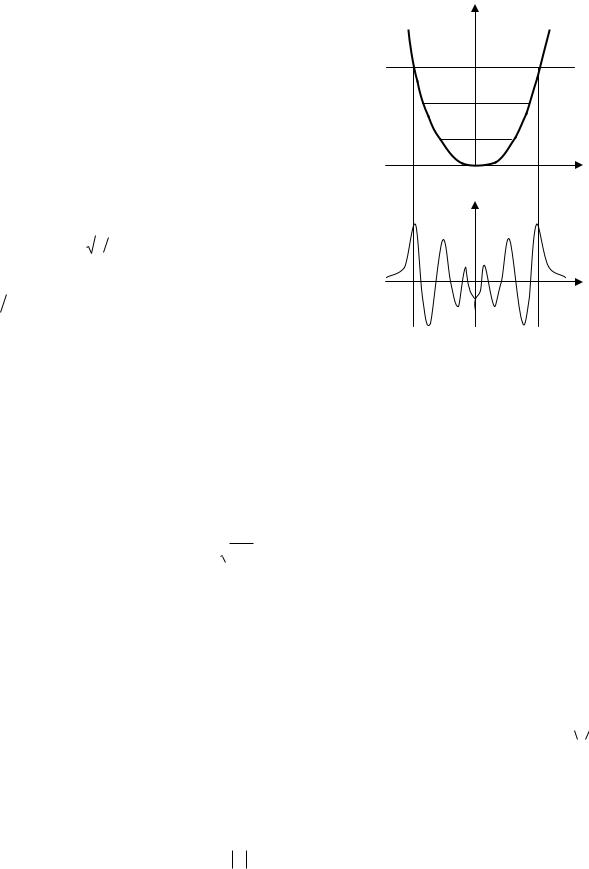
21.Частица движется слева направо в одномерном потенциальном поле, показанном на рис.2.1. Левее барьера, высота которого U = 15 эВ, полная энергия частицы равна 20 эВ. Как
изменится дебройлевская длина волны частицы при переходе через барьер?
22.Частица движется справа налево в одномерном потенциальном поле, показанном на рис.2.1. Правее барьера, высота которого U = 15 эВ, кинетическая энергия частицы равна 5 эВ. Как изменится
дебройлевская длина волны частицы при переходе через барьер?
23.Какую энергию необходимо дополнительно сообщить электрону, чтобы его дебройлевская длина волны уменьшилась со 100 до 50 пм?
24.Как нужно изменить энергию нейтрона, чтобы его дебройлевская длина волны увеличилась с
50 до 100 пм?
25.Как изменится дебройлевская длина волны частицы, если ее кинетическая энергия уменьшится в 3 раза?
3. СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ ГЕЙЗЕНБЕРГА
Соотношение неопределенностей для координаты x и проекции импульса px на ось x |
|
x px , |
(3.1) |
где x и px – неопределенность координаты и проекции импульса частицы, ћ = h/2π; h – постоянная Планка. Соотношение неопределенностей для энергии E и времени t имеет вид
E t . |
(3.2) |
Примеры решения задач
1. Масса движущегося электрона в три раза больше его массы покоя. Чему равна минимальная
неопределенность координаты электрона?
Решение. Учитывая, что p mV , где m – масса, V – скорость частицы, получим из (3.1)x  m Vx . Поскольку неопределенность скорости Vx, как и сама скорость, не может превышать
m Vx . Поскольку неопределенность скорости Vx, как и сама скорость, не может превышать
9

vk.com/club152685050 | vk.com/id446425943
скорость света |
c |
в вакууме, то |
xmin mc . |
Согласно условию |
m = 3m0. Подставляя, |
получим |
||||
x |
3m c |
= 1,28 10–13 м. |
|
|
|
|
|
|
||
min |
0 |
|
|
|
|
|
|
|
|
|
|
2. Среднее |
время |
жизни |
возбужденных состояний |
атома |
составляет |
10 нс. Вычислить |
|||
естественную |
ширину |
спектральной линии |
( = 0,7 мкм), |
соответствующую |
переходу |
между |
||||
возбужденными уровнями атома. |
|
|
|
|
|
|
||||
|
Решение. При переходе электрона из одного стационарного состояния в другое излучается (или |
|||||||||
поглощается) энергия, равная hc/λ = En – Ek, где En и Ek – энергии соответствующих состояний атома; –
длина волны излучения. Отсюда следует, что неопределенность длины волны излучения связана с неопределенностью энергии уровней En и Ek атома соотношением hcΔλ/λ2 = En + Ek. Согласно соотношению неопределенностей Гейзенберга (3.2), E t , где t – неопределенность момента времени перехода атома из одного стационарного состояния в другое. Поскольку t не превышает среднего времени
жизни возбужденного состояния атома τ, то минимальная неопределенность энергии возбужденных уровней равна Emin  . Минимальная неопределенность длины волны излучения (естественная ширина
. Минимальная неопределенность длины волны излучения (естественная ширина
спектральной линии) равна min 2  2 c 1
2 c 1 n 1
n 1 k . Если одно из состояний (k), между которыми совершается переход, является основным, то Δλmin = λ2/(2πcτn), так как для основного состояния τk = ∞. Для возбужденных состояний с одинаковым временем жизни τn = τk = τ имеем Δλmin = λ2/(πcτ). Подставляя числовые данные, получим Δλmin = 5,2 10–14 м.
k . Если одно из состояний (k), между которыми совершается переход, является основным, то Δλmin = λ2/(2πcτn), так как для основного состояния τk = ∞. Для возбужденных состояний с одинаковым временем жизни τn = τk = τ имеем Δλmin = λ2/(πcτ). Подставляя числовые данные, получим Δλmin = 5,2 10–14 м.
Задачи для самостоятельного решения
1.Среднее расстояние электрона от ядра в невозбужденном атоме водорода равно 52,9 пм. Вычислить минимальную неопределенность скорости электрона.
2.Используя соотношение неопределенностей, показать, что в ядре не могут находиться
электроны. Линейные размеры ядра принять равными 5,8 10–15 м.
3.Чему равна неопределенность координаты покоящегося электрона?
4.Вычислить неопределенность координаты покоящегося протона?
5.Кинетическая энергия протона равна его энергии покоя. Чему равна при этом минимальная неопределенность координаты протона?
6.Масса движущегося электрона в два раза больше его массы покоя. Вычислить минимальную неопределенность координаты электрона.
7.Чему равна минимальная неопределенность координаты фотона, соответствующего видимому излучению с длиной волны 0,55 мкм.
8.Среднее время жизни эта-мезона составляет 2,4 10–19 с, а его энергия покоя равна 549 МэВ.
Вычислить минимальную неопределенность массы частицы.
10
vk.com/club152685050 | vk.com/id446425943
9.Среднее время жизни возбужденного состояния атома равно 12 нс. Вычислить минимальную неопределенность длины волны λ = 0,12 мкм излучения при переходе атома в
основное состояние.
10.Естественная ширина спектральной линии λ = 0,55 мкм, соответствующей переходу атома в
основное состояние, равна 0,01 пм. Определить среднее время жизни возбужденного состояния атома.
11.Ширина следа электрона (обладающего кинетической энергией 1,5 кэВ) на фотопластинке,
полученного с помощью камеры Вильсона, |
составляет |
х = 1 мкм. Определите, можно ли по данному |
|
следу обнаружить отклонение в движении электрона от законов классической механики. |
|||
12. Электронный |
пучок ускоряется |
в электронно-лучевой трубке разностью потенциалов |
|
U = 1 кВ. Известно, что |
неопределенность |
скорости |
составляет 0,1 % от ее числового значения. |
Определите неопределенность координаты электрона. Являются ли электроны в данных условиях квантовой или классической частицей?
13.Определите отношение неопределенностей скорости электрона, если его координата установлена с точностью до 10–5 м, и пылинки массой m = 10–12 кг, если ее координата установлена с
такой же точностью.
14.Электронный пучок ускоряется разностью потенциалов U = 200 В. Определить, можно ли
одновременно измерить траекторию электрона с точностью до 100 пм (с точностью порядка диаметра атома) и его скорость с точностью до 10 %.
15.Электрон движется в атоме водорода по первой боровской орбите. Принимая, что допускаемая неопределенность скорости составляет 10 % от ее числового значения, определите неопределенность координаты электрона. Применимо ли в данном случае для электрона понятие траектории?
16.Используя соотношение неопределенностей в форме (3.1), оцените минимально возможную полную энергию электрона в атоме водорода. Примите неопределенность координаты равной радиусу атома.
17.Оцените размытость энергетического уровня в атоме водорода: а) для основного состояния; б) для возбужденного состояния (время его жизни равно 10–8 с).
18.Длина волны λ излучаемого атомом фотона составляет 0,6 мкм. Принимая время жизни возбужденного состояния t = 10–8 с, определите отношение естественной ширины энергетического
уровня, на который был возбужден электрон, к энергии, излученной атомом.
19.Принимая, что электрон находится внутри атома диаметром 0,3 нм, определите (в электронвольтах) неопределенность энергии данного электрона.
20. При движении вдоль оси х скорость оказывается определенной с точностью Vx = 1 см/с. Оценить неопределенность координаты x: а) для электрона, б) для броуновской частицы массы m = 10–
13г, в) для дробинки массы m = 0,1 г.
21.Электрон с кинетической энергией Е = 4 эВ локализован в области размером L = 1 мкм.
Оценить относительную неопределенность его скорости.
11
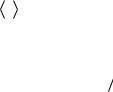
vk.com/club152685050 | vk.com/id446425943
22. Оценить наименьшие ошибки, с которыми можно определить скорость электрона, протона и шарика массы 1 мг, если координаты частиц и центра шарика установлены с неопределенностью 1 мкм.
23. Свободный электрон в момент времени t = 0 локализован в области x0 = 0,1 нм. Оценить ширину области локализации этого электрона спустя t = 1 с.
24.След пучка электронов на экране электронно-лучевой трубки имеет диаметр d = 0,5 мм. Расстояние от электронной пушки до экрана L = 20 см, ускоряющее напряжение U = 10 кВ. Оценить
неопределенность координаты электрона на экране.
25.Оценить с помощью соотношения неопределенностей минимальную кинетическую энергию электрона, локализованного в области размером L = 0,20 нм.
4. ВВЕДЕНИЕ В КВАНТОВУЮ МЕХАНИКУ. УРАВНЕНИЕ ШРЕДИНГЕРА
Поведение частицы в микромире описывается волновой функцией ψ, которая в общем случае является комплексной величиной. Квадрат модуля этой функции определяет вероятность того, что частица находится в бесконечно малом объеме dV вблизи рассматриваемой точки с координатами x,y,z:
dw |
|
x |
|
2 dV * x x dV |
(4.1) |
|
|
где ψ* – комплексно сопряженная величина. Вероятность найти частицу в конечном объеме V равна
W dw |
|
|
|
2 dV |
(4.2) |
|
|
||||
|
|
|
|||
V |
|
||||
Волновая функция однозначна, непрерывна, ограничена и на бесконечности стремится к нулю.Так как вероятность найти частицу во всем пространстве равна 1, то имеет место условие нормировки
|
|
|
|
2 dV 1 , |
(4.3) |
|
|
||||
V |
|
||||
где интегрирование ведется по всему пространству.
Каждой физической величине q, характеризующей состояние частицы с волновой функцией ψ, ставится в соответствие оператор q такой, что среднее значение q вычисляется по формуле
|
* |
|
|
q q dV . |
|
(4.4) |
|
V |
|
|
|
Оператор координаты x (и оператор любой функции, зависящей только от координат) совпадает |
|||
с самой координатой х (функцией). Действие оператора импульса |
p i d |
dx i |
(i – мнимая |
|
|
|
|
единица) сводится к дифференцированию. Действие оператора полной энергии
12

vk.com/club152685050 | vk.com/id446425943
|
|
2 |
ˆ |
|
2 |
|
|
|
|
p |
|
|
|
2 |
|
|
|||
H |
|
|
U |
|
|
|
|
U . |
(4.5) |
2m |
2m |
|
|||||||
|
|
|
|
|
|
||||
на волновую функцию дает энергию частицы Е и т.д.
Волновая функция удовлетворяет временнóму уравнению Шредингера – аналогу второго закона Ньютона
|
2 |
2 U i |
. |
(4.6) |
|
||||
|
2m |
|
t |
|
Здесь m – масса частицы, U – функция координат и времени, градиент которой, взятый с обратным знаком, равен силе, действующей на частицу. Если U не зависит явно от времени, то она имеет смысл
потенциальной энергии. В этом случае волновая функция может быть представлена в виде произведения двух множителей, один из которых зависит только от координат, а второй – от времени:
x, y, z,t x, y, z exp i Et , |
(4.7) |
где Е – полная энергия частицы. Временнóе уравнение Шредингера (4.3) при этом переходит в стационарное
2 |
2m |
E U 0 . |
(4.8) |
|
|||
|
2 |
|
|
Решение уравнения Шредингера означает отыскание собственных функций ψi (i – нумерует собственные функции) оператора H и их собственных значений Ei. Если движение частицы ограничено в
пространстве, то решения уравнения существуют лишь при дискретных значениях энергии Е. В случае отсутствия пространственных ограничений уравнение имеет решения, соответствующие любым значениям Е.
Пусть ψ1, ψ2, …, ψi,…, ψn есть набор собственных функций частицы. В каждом из этих состояний ψi физическая величина q имеет определенное значение qi. Однако частица может находиться и в
n
состоянии Ci i , где Ci – не зависящие от координат числа. Число слагаемых в сумме равно
i 1
числу различных собственных функций. Величина q в этом состоянии не имеет определенного значения
– при измерениях будет получаться одно из значений qi. Вероятность получить результат qi равна Ci 2 ,
n
сумма всех таких вероятностей равна единице: Ci 2 1. Зная вероятности различных значений
i 1 |
|
|
||
n |
|
|
||
величины q, можно найти среднее значение этой величины в состоянии ψ: q |
|
Ci |
|
2 qi . Это есть |
|
|
|||
i 1 |
|
|
||
выражение принципа суперпозиции в квантовой механике. |
|
|
||
13
vk.com/club152685050 | vk.com/id446425943
U
Примеры решения задач
1. Записать уравнение Шредингера для гармонического
осциллятора.
Решение. Гармоническим осциллятором называют частицу, совершающую одномерное движение под действием квазиупругой силы F = –kx. Потенциальная энергия такой частицы равна (рис.4.1)
U = kx2/2. |
Собственная |
|
|
частота |
классического гармонического |
|||||||||||||
осциллятора равна |
|
|
|
|
, где m – масса частицы. Выразив k |
|||||||||||||
|
k m |
|||||||||||||||||
через m |
и ω, |
получим |
|
U = mω2x2/2. |
В одномерном случае |
|||||||||||||
2 d 2 dx2 . |
Поэтому уравнение Шредингера для осциллятора |
|||||||||||||||||
имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
2 |
|
|
|
|
|
|
|
|
|
2 |
x |
2 |
|
|
|
|
|
|
|
|
2m |
|
m |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
0 . |
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
||||
En
E0
0 |
x |
ψ
x
Рис.4.1
Можно показать, что собственные значения этого уравнения суть En кол n 1 2 , где кол – собственная частота колебаний. Энергия при n = 0 называется энергией нулевых колебаний. Как
2 , где кол – собственная частота колебаний. Энергия при n = 0 называется энергией нулевых колебаний. Как
видно на рис.4.1, спектр собственных энергий эквидистантный, т.е. расстояния между соседними уровнями не зависят от n. Волновая функция основного состояния
0 4
 exp x2
exp x2 2 ,
2 ,
где m  . Она также приведена на рис.4.1. Как видно, в отличие от классического случая, существует
. Она также приведена на рис.4.1. Как видно, в отличие от классического случая, существует
конечная вероятность обнаружения частицы за пределами дозволенной области, показанной пунктиром на рис.4.1.
2. Волновая функция основного состояния атома водорода имеет вид A exp r a , где a –
a , где a –
константа (радиус Бора). Найти: а) значение константы А; б) плотность вероятности нахождения электрона на расстоянии r от ядра; в) наиболее вероятное расстояние rвер электрона от ядра; г) среднее расстояние  r
r 
электрона от ядра; д) вероятность того, что электрон находится на расстоянии от ядра, превышающем ηа (η – константа).
Решение. а) Значение константы А найдем из условия нормировки
2 dV 1.
V
14

vk.com/club152685050 | vk.com/id446425943
Отметим, что волновая функция сферически симметрична, т.е. не зависит от углов. Поэтому элементарный объем равен dV 4 r2dr . Подставляя выражения для объема и волновой функции в
условие нормировки, получим
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
A2 e 2r a 4 r 2 dr 4 A2 r 2 e 2r a dr 1. |
||||||||
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
Интеграл равен |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
2! |
|
a |
3 |
|
|
|
|
|
|
|
|
r 2e 2r a dr |
|
|
. |
||
|
|
|
|
3 |
|
|
||||||
|
|
|
|
0 |
2 a |
4 |
|
|||||
Тогда 4 A2 |
a3 |
1. Отсюда A |
|
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4 |
|
|
|
a3 |
|
|
|
|
|
|||
б) Вероятность найти |
|
электрон на |
расстоянии от r до r + dr от ядра |
|||||||||
dW 2 dV 4 A2r2e 2r adr . Плотность вероятности нахождения электрона на расстоянии r от ядра
adr . Плотность вероятности нахождения электрона на расстоянии r от ядра
w |
dW |
4 A2r 2e 2r a |
4 |
r 2e 2r a . |
|
dr |
a3 |
||||
|
|
|
в) Наиболее вероятное расстояние электрона от ядра соответствует максимуму функции w(r):
dw 0 . Беря производную, получим dr
8r |
|
e |
2r |
a |
|
r |
|
|
вер |
вер |
1 |
|
вер |
|
0 . |
||
|
3 |
|
|
|||||
a |
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
||
Отсюда rвер = a.
г) Среднее расстояние электрона от ядра равно  r
r  r 2 dV . Подставим выражения для объема и
r 2 dV . Подставим выражения для объема и
|
|
|
|
0 |
|
волновой функции |
|
|
|
|
|
|
1 |
|
|
4 |
|
r r |
|
e 2r a 4 r 2dr |
r3e 2r a dr . |
||
a |
3 |
3 |
|||
0 |
|
|
a |
0 |
|
|
|
|
|
Используя интегрирование по частям
xnebxdx 1 b xnebx n
b xnebx n b xn 1ebxdx ,
b xn 1ebxdx ,
получим для среднего расстояния электрона от ядра r = 3a/2.
д) Используем полученное значение константы А для нахождения вероятности того, что электрон расположен от ядра на расстоянии большем, чем ηa:
15
vk.com/club152685050 | vk.com/id446425943
W dW 4 r 2e 2r a dr
a dr
a a3
4 r 2e 2r a dr .
a dr .
a3 a
Беря интеграл, получим W e 2 |
1 2 2 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
3. Волновая |
функция, |
описывающая |
состояние |
частицы |
в |
E |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
одномерной потенциальной яме с бесконечно высокими стенками, имеет |
|
|
|
U → ∞ |
|||||||||||||||||||
вид ψ(x) = Asin(kx). |
Определите |
а) вид собственной волновой функции |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
ψn(x); б) коэффициент А, исходя из условия нормировки. |
|
|
|
|
|
|
|
|
|
||||||||||||||
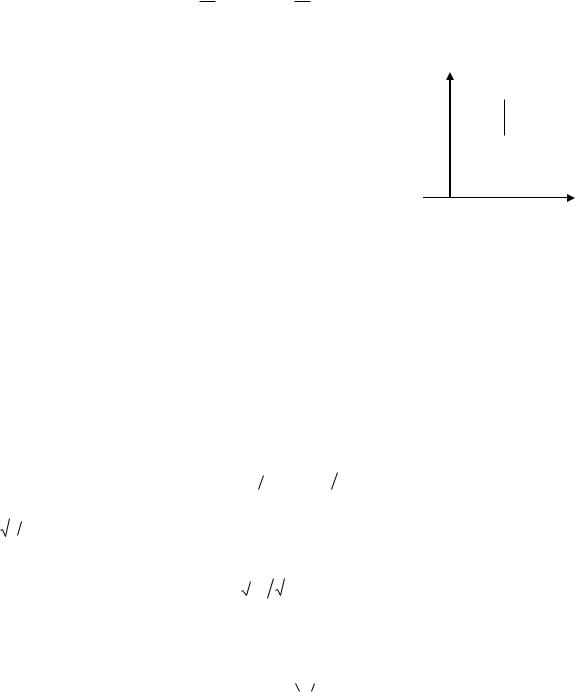
Решение. Схема такой ямы приведена на рис.4.2. Так как стенки |
|
|
|
|
|
||||||||||||||||||
ямы бесконечно высоки, то за |
пределами |
потенциальной |
ямы частица |
0 |
|
|
|
|
|||||||||||||||
|
|
L |
x |
||||||||||||||||||||
оказаться не |
|
может |
и волновая функция |
равна нулю: ψ(x < 0) = 0 |
и |
|
|
Рис.4.2 |
|
||||||||||||||
ψ(x > L) = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) Внутри ямы волновая функция не равна нулю: ψ(0 x < L) ≠ 0. В силу непрерывности волновой |
|||||||||||||||||||||||
функции на границах должны выполняться соотношения ψ(0) = ψ(L) = 0. Подставим выражение для |
|||||||||||||||||||||||
волновой функции ψ(L) = Asin(kL) = 0. Это возможно в том случае, если аргумент синуса |
kL n . |
||||||||||||||||||||||
Отсюда k = πn/L, и собственные волновые функции равны ψn(x) = Asin(πnx/L). |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б) Запишем условие нормировки |
|
n x |
|
2 dx 1 . |
Подставляя собственные волновые функции, |
||||||||||||||||||
|
|
||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
A2 sin 2 n x L dx A2 L 2 1 . |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 L . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4. Состояние частицы, |
находящейся в бесконечно глубокой прямоугольной потенциальной яме |
||||||||||||||||||||||
шириной L, |
задано |
волновой |
|
|
|
|
|
|
|
|
|
|
|
|
или |
нет определенной |
|||||||
|
|
|
|
|
|
|
5 |
|
|
||||||||||||||
|
|
|
|
30 |
|
|
|
||||||||||||||||
функцией x |
|
L |
x L x . Обладает |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
энергией частица в этом состоянии? В случае отрицательного ответа сформулировать общее выражение для: а) вероятности найти при измерении энергию частицы Е равной энергии собственного состояния с
номером n En n 2  2mL2 ; б) средней энергии частицы
2mL2 ; б) средней энергии частицы  E
E  .
.
Решение. Так как эта функция не является собственной функцией уравнения Шредингера для частицы в яме, то частица не имеет определенной энергии в этом состоянии. Это состояние является
суперпозицией нескольких собственных состояний Ci i .
i
а) Вероятность получить при измерении энергию частицы, равной En,
|
|
|
|
L |
|
2 |
|
P |
|
C |
2 |
|
|
* |
dx . |
n |
|
n |
|
|
n |
|
|
|
|
|
|
|
|
||
|
|
|
|
0 |
|
|
|
16

vk.com/club152685050 | vk.com/id446425943
Используя собственные функции n 
 2
2 L sin n x
L sin n x L , получим
L , получим
P 2 |
|
L3 L sin n x L x L x dx . |
15 |
||
n |
|
|
|
|
0 |
n
б) Средняя энергия частицы находится как взвешенное среднее  E
E Ei Ci 2 .
Ei Ci 2 .
i 1
Задачи для самостоятельного решения
1.Записать уравнение Шредингера для свободной частицы.
2.Записать уравнение Шредингера для электрона в атоме водорода.
3.Волновая функция, описывающая некоторую частицу, может быть представлена как
произведение координатной функции |
ψ и |
временного |
множителя, т.е. |
имеет вид |
x,t x exp iEt . Покажите, что |
плотность |
вероятности |
нахождения частицы |
определяется |
только координатной ψ-функцией.
Для волновой функции основного состояния водородного атома, имеющей вид ψ = Aexp(–r/a), где a – боровский радиус:
4. Найти среднее значение потенциальной энергии электрона.
5.Найти среднее значение модуля кулоновской силы, действующей на электрон.
6.Найти средний электростатический потенциал, создаваемый электроном в центре атома
водорода.
7.Вычислить вероятность того, что электрон в этом состоянии находится от ядра на расстоянии, превышающем а) 2а; б) 5а и в) 10а.
8.Вычислить вероятность того, что электрон в этом состоянии находится от ядра на расстоянии
a < r < 2a.
9.Найти наиболее вероятное расстояние частицы от центра.
10.Найти среднее расстояние частицы от центра.
11.Рассматривая математический маятник массой m = 100 г и длиной L = 0,5 м в виде
гармонического осциллятора, определите классическую амплитуду А маятника, соответствующую энергии нулевых колебаний этого маятника, находящегося в поле тяготения Земли.
Волновая функция основного состояния гармонического осциллятора имеет вид0 4
 exp x2
exp x2 2 , где α = m /ħ:
2 , где α = m /ħ:
12.Найти среднее значение координаты х.
13.Найти среднее значение импульса для этого состояния.
14.Найти среднее значение потенциальной энергии этого состояния.
17

vk.com/club152685050 | vk.com/id446425943
15. Найти среднюю энергию (в электронвольтах) электромагнитного колебания при температуре
3000 К для длин волн λ, равных: а) 500 мкм, б) 50 мкм, в) 5 мкм, г) 0,5 мкм. |
Сравнить найденные |
значения с величиной kT. |
|
16. Показать, что в основном состоянии гармонического осциллятора p |
x = ħ/2, где p и x – |
среднеквадратичные отклонения импульса и координаты от их средних. Учесть, |
что x2 = x2 – x 2 и |
p2 = p2 – p 2.
Волновая функция некоторой частицы имеет вид ψ = Aexp(–r2/2a2), где r – расстояние от частицы до силового центра; а – константа:
17.Найти наиболее вероятное расстояние частицы от центра.
18.Найти среднее значение координаты x .
Частица в момент времени t = 0 находится в состоянии ψ = Aexp(–x2/a2 + ikx), где А и а –
некоторые положительные постоянные:
19.Найти среднее значение проекции импульса px .
20.Найти нормировочный коэффициент А и область, в которой частица локализована.
21.Определить энергию электрона атома водорода в состоянии, для которого волновая функция имеет вид ψ(r) = A(1 + ar)exp(–αr), где А, а и α – некоторые постоянные.
22.Известно, что нормированная собственная волновая функция, описывающая состояние электрона в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками, имеет
вид n x 
 2
2 L sin nx
L sin nx L , где L – ширина ямы. Определите среднее значение координаты х электрона.
L , где L – ширина ямы. Определите среднее значение координаты х электрона.
23.Состояние частицы, находящейся в бесконечно глубокой прямоугольной потенциальной яме ширины L, задано волновой функцией ψ(x) = Ax(L – x). Найти нормировочный коэффициент А.
24.Состояние частицы, находящейся в бесконечно глубокой прямоугольной потенциальной яме
шириной L, задано волновой функцией |
|
|
|
|
|
|
5 |
||||
|
|||||
x 30 |
|
L |
x L x . Найти вероятность того, что при |
||
|
|
|
|
|
|
измерении энергия частицы окажется равной Е1. Чему равна вероятность получить при измерении отличное от Е1 значение энергии частицы?
25. Волновая функция основного состояния частицы в бесконечно глубокой потенциальной яме имеет вид 1 x 
 2
2 L sin x
L sin x L , где L – ширина ямы. Покажите, что Δx2 Δp2 ~ ħ2. Учесть, чтоΔx2 = x2 – x 2 и Δp2 = p2 – p 2.
L , где L – ширина ямы. Покажите, что Δx2 Δp2 ~ ħ2. Учесть, чтоΔx2 = x2 – x 2 и Δp2 = p2 – p 2.
5. ПОТЕНЦИАЛЬНАЯ ЯМА И ПОТЕНЦИАЛЬНЫЙ БАРЬЕР.
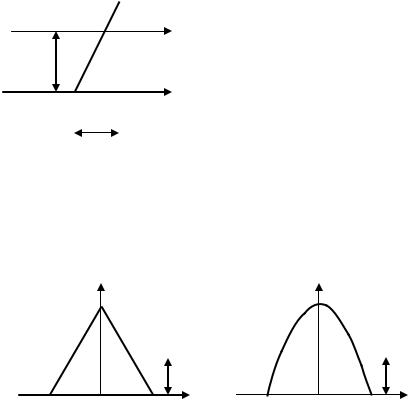
Решение уравнения Шредингера для частицы в прямоугольной бесконечно глубокой потенциальной яме (рис.5.1) шириной L дает для энергии лишь дискретные значения
18
vk.com/club152685050 | vk.com/id446425943
|
|
|
|
|
|
E |
|
|
n2 2 2 |
, |
|
|
5.1) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
n |
|
2mL2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где число n нумерует возможные значения энергии, |
n = 1, 2, 3,…-целое число. |
При этом волновая |
||||||||||||||
функция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n x |
|
|
sin n x L . |
|
(5.2) |
||||
|
|
|
|
|
|
|
2 |
L |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Расстояние |
между |
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
уровнями с номерами n и n + 1 |
||
|
|
U → ∞ |
|
|
U0 |
|
|
|
|
|
|
|
|
зависит от n |
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
E En 1 En 2 2 2n 1 2mL2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
I |
|
II |
|
|
|
|
|
|
|
. |
(5.3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим |
движение |
|
0 |
L |
x |
0 |
|
|
|
x |
|
||||||||
|
|
|
|
частицы с |
энергией Е в поле |
|||||||||||
|
Рис.5.1 |
|
|
|
Рис.5.2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
потенциального |
барьера |
|
бесконечной ширины (рис.5.2) и высоты U0. Если E < U0, то в стационарном режиме вся энергия падающей волны отражается, однако под ступенькой (x > 0) волновая функция не равна нулю, а экспоненциально затухает с ростом координаты x. Это соответствует наличию коэффициента
преломления
|
|
n 1 2 k2 k1 , |
(5.4) |
где k12 2mE 2 |
и k22 2m E U0 |
2 – волновые числа, соответствующие |
движению частицы в |
областях I и II. |
|
|
|
Если U0 < E, то частица частично отражается, а частично проходит через барьер. Поэтому можно ввести коэффициент отражения R и коэффициент прохождения D.
Коэффициент отражения барьера
R |
|
k |
k |
2 |
k |
k |
2 |
|
|
2 . |
(5.5) |
|
|
||||||||||
|
|
1 |
|
1 |
|
|
|
|
|
||
Коэффициент пропускания барьера D равен отношению доли прошедшей волны к падающей: |
|||||||||||
D 4k1k2 |
k1 |
k2 2 . |
(5.6) |
||||||||
Для коэффициентов отражения и прохождения выполняется |
соотношение |
R + D = 1. В |
|||||||||
классическом случае для E > U0 всегда D = 1 и R = 0.
Если кантовая частица массой m, двигаясь в области I с энергией Е, встречает на своем пути потенциальный барьер (рис.5.3) шириной L и высотой U0, то она может отразиться и остаться в области I. Однако существует конечная вероятность того, что она окажется в области III, даже если E < U0. Этот
эффект называется туннельным эффектом. В области II происходит затухание волновой функции.
19

vk.com/club152685050 | vk.com/id446425943
|
Вероятность |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
прохождения |
частицы |
|
через |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
барьер |
– |
|
коэффициент |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
) |
|
I |
|
II |
III |
|
|
|
|
|
|
|
|
E |
|||||||
прозрачности |
потенциального |
|
|
|
|
|
|
|
|
|
|
|||||||||||
(x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
барьера D равен |
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
2L |
|
|
|
|
|
0 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
x2 |
x |
||||||
|
D D0 |
exp |
|
|
2m U0 E |
|
L |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
Рис.5.3 |
|
|
|
|
Рис.5.4 |
|
||||||
|
|
, |
|
|
|
(5.7) |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где m и Е – масса и энергия частицы, падающей на барьер; U0 – высота барьера; L – ширина барьера; коэффициент D0 определяется природой барьера и обычно слабо отличается от единицы D0 ≈ 1.
Если барьер имеет произвольную форму (рис.5.4), то его можно разбить на ряд прямоугольных барьеров. Суммарное действие таких барьеров приводит к формуле
|
x2 |
|
|
|
D D0 exp 2 |
|
2m U E |
dx . |
(5.8) |
|
x1 |
|
|
|
|
|
|
|
Пределы интегрирования определяются из условия U(x) = E.
Примеры решения задач
1. Электрон находится в потенциальной яме, шириной L. Найти вероятность того, что электрон, находящийся в возбужденном состоянии (n = 2), будет обнаружен в средней трети ямы.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
Решение. |
|
Вероятность найти частицу в интервале x1 < x < x2 |
есть W 2 |
|
n x |
|
2 dx , где ψn(x) – |
||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
нормированная |
собственная |
волновая |
|
функция. |
Для |
прямоугольной ямы |
n x |
|
sin nx L . |
||||||||||||||||||||||||||
|
2 L |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Учитывая, что n = 2, |
получим |
W 2 |
L 2sin 2 2 x L dx . |
По условию x1 = L/3 |
|
и x2 = 2L/3. Проведем |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
замену sin 2 2 x L 1 cos 4 x L 2 и разобьем интеграл на два |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
2 2L 3 |
|
2 |
|
2 |
x |
|
1 |
|
2L |
3 |
2L 3 |
|
4 |
x |
|
|
1 |
|
|
1 |
|
8 |
|
|
4 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|||||||||
W |
|
|
|
sin |
|
|
|
|
dx |
|
|
|
|
dx |
|
cos |
|
|
dx |
|
|
|
sin |
|
|
|
|
. |
|||||||
|
|
L |
|
|
L |
|
L |
|
|
|
|
L |
|
|
3 |
|
4 |
3 |
|
3 |
|
|
|||||||||||||
|
|
|
L 3 |
|
|
|
|
|
|
|
|
L 3 |
L 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Вычисляя, получим W = 0,195.
2. Частица находится в бесконечно глубокой одномерной потенциальной яме шириной L на
втором энергетическом уровне. В каких точках ямы плотность вероятности обнаружения частицы совпадает с классической плотностью вероятности.
20

vk.com/club152685050 | vk.com/id446425943
Решение. Волновая функция ψ, описывающая состояние частицы в бесконечно глубокой одномерной потенциальной яме шириной L, имеет вид n x 
 2
2 L sin nx
L sin nx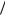 L , где n – номер энергетического уровня (n = 1, 2, …); x – координата частицы в яме (0 ≤ x ≤ L). Согласно физическому смыслу волновой функции, плотность вероятности w обнаружения частицы в точке с координатой x, равна w = |ψ|2. Если частица находится на втором энергетическом уровне (n = 2), то w2 = (2/L)sin2(2πx/L).
L , где n – номер энергетического уровня (n = 1, 2, …); x – координата частицы в яме (0 ≤ x ≤ L). Согласно физическому смыслу волновой функции, плотность вероятности w обнаружения частицы в точке с координатой x, равна w = |ψ|2. Если частица находится на втором энергетическом уровне (n = 2), то w2 = (2/L)sin2(2πx/L).
Следуя принципу соответствия Бора, выражение для классической плотности вероятности получается при n → ∞: w∞ = 1/L. Приравнивая, получим sin2(2πx/L) = 1/2. Решая это уравнение, найдем x k 1 4 L
4 L 2 , где k принимает значения 0, ±1, ±2, … В пределах ямы таких точек четыре x = (L/8;
2 , где k принимает значения 0, ±1, ±2, … В пределах ямы таких точек четыре x = (L/8;
3L/8; 5L/8; 7L/8).
3. Электрон с энергией Е = 4,9 эВ движется в положительном направлении оси x и падает на потенциальный барьер высотой U0 = 5 эВ и шириной L. При какой ширине барьера вероятность W
прохождения электрона через барьер будет равна 0,2?
Решение. Вероятность прохождения W частицы через барьер по смыслу есть не что иное, как его
коэффициент прозрачности D. |
Поэтому W D exp 2L |
|
|
|
. Для удобства вычислений |
||||||||||||||||||||
|
2me U0 |
E |
|||||||||||||||||||||||
логарифмируем |
ln W 2L |
|
. Поменяем знаки |
|
правой |
|
и левой |
частей |
и |
найдем |
|||||||||||||||
2me U0 E |
|
|
|||||||||||||||||||||||
L |
|
ln 1 W |
|
|
= 4,95 10 |
–10 |
м. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2m U |
0 |
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Поток электронов, каждый из которых имеет энергию |
Е = 100 эВ, |
падает |
на |
барьер |
|||||||||||||||||||
бесконечной ширины высотой U0 < E. Определить высоту потенциального барьера U0, если известно, |
|||||||||||||||||||||||||
что 4 % падающих на барьер электронов отражаются. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
Решение. |
Коэффициент отражения барьера R |
|
k |
k |
2 |
k |
k |
2 |
|
|
2 , где k1 и k2 – |
волновые |
|||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
||||
числа электрона, отвечающие движению электрона в областях I и II соответственно. Так как координата электрона точно не известна, то в соответствии с принципом неопределенностей Гейзенберга точно
известен |
импульс |
|
электрона и, соответственно, его кинетическая |
энергия. В |
левой области |
|||||||||||||||||||||||||
k1 1 |
|
|
. В |
|
правой |
области |
кинетическая энергия |
равна |
E – |
U0 и k2 1 |
|
|
|
. |
||||||||||||||||
2me E |
|
2me E U 0 |
||||||||||||||||||||||||||||
Подставив в выражение для R и разделив на |
|
, получим |
R 1 |
|
|
|
|
|
|
2 |
1 |
|
|
2 . |
||||||||||||||||
2me E |
1 U 0 |
E |
1 U 0 E |
|||||||||||||||||||||||||||
Преобразуем |
|
|
|
1 |
|
|
1 |
|
|
. Выразим отсюда U |
|
1 |
1 |
|
|
1 |
|
2 E = 55,6 эВ. |
||||||||||||
1 U |
|
E |
|
R |
|
R |
|
|
R |
R |
||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задачи для самостоятельного решения
1. Альфа-частица находится в бесконечно глубокой одномерной потенциальной яме. Чему равна
ширина ямы, если минимальная энергия частицы составляет 6 МэВ.
21
vk.com/club152685050 | vk.com/id446425943
2.Электрон находится в бесконечно глубокой одномерной потенциальной яме шириной 0,1 нм. Вычислить длину волны излучения при переходе электрона со второго на первый энергетический уровень.
3.Протон находится в бесконечно глубокой одномерной потенциальной яме шириной 0,01 пм. Вычислить длину волны излучения при переходе протона с третьего на второй энергетический уровень.
4.Атом водорода находится в бесконечно глубокой одномерной потенциальной яме шириной 0,1 м. Вычислить разность энергий соседних уровней, соответствующих средней энергии теплового
движения атома при температуре 300 К.
5.Частица находится в бесконечно глубокой одномерной потенциальной яме шириной L в
основном состоянии. В каких точках ямы плотность вероятности обнаружения частицы совпадает с классической плотностью вероятности?
6.Частица находится в бесконечно глубокой одномерной потенциальной яме шириной L в
основном состоянии. Чему равно отношение плотности вероятности обнаружения частицы в центре ямы
кклассической плотности вероятности?
7.Частица находится в бесконечно глубокой одномерной потенциальной яме шириной L в
первом возбужденном состоянии. В каких точках ямы плотность вероятности обнаружения частицы максимальна, а в каких минимальна?
8.Определите среднее значение импульса в основном состоянии электрона в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками.
9.Определите среднее значение квадрата импульса в основном состоянии электрона в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками.
10.Частица находится в бесконечно глубокой одномерной потенциальной яме шириной L на втором энергетическом уровне. Определить вероятность обнаружения частицы в пределах от 0 до L/3.
11.Частица находится в бесконечно глубокой одномерной потенциальной яме шириной L в основном состоянии. Найти отношение вероятностей нахождения частицы в пределах от 0 до L/4 для
первого и второго энергетических уровней.
12.Частица находится в бесконечно глубокой одномерной потенциальной яме шириной L в основном состоянии. Найти отношение вероятностей нахождения частицы в пределах от 0 до L/3 и от
L/3 до 2L/3.
13.Оценить разность En двух соседних уровней энергии при n >> 1 для молекулы газа, находящегося в сосуде, приняв массу молекулы m = 10–26 кг, а размер сосуда L = 10 см (считать сосуд
бесконечно глубокой потенциальной ямой). Сравнить со средней кинетической энергией молекул при комнатной температуре Т = 300 К.
14.Оценить разность En двух соседних уровней энергии при n >> 1 для электрона, локализованного в атоме с линейными размерами L ~ 10–10 м (атом считать бесконечно глубокой
потенциальной ямой).
15.Для электрона с энергией E = 1 эВ оценить эффективную глубину его проникновения под
барьер высоты U0 = 5 эВ.
22
vk.com/club152685050 | vk.com/id446425943
|
|
|
|
|
U0 |
|
|
|
|
|
16. Прямоугольный потенциальный бартер имеет ширину L = 0,1 нм. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определите (в электронвольтах) |
разность энергий U0 – E, |
при |
которой |
|||||||||||
|
|
E |
|
|
|
|
|
|
вероятность прохождения электрона сквозь барьер равна 0,5. |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
17. Протон с энергией 5 эВ движется вдоль оси х, встречая на |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
своем пути прямоугольный потенциальный барьер высотой U0 = 10 эВ и |
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
шириной |
L = 0,1 нм. |
Определите вероятность |
прохождения протоном |
||||||||||||
|
|
|
|
|
L |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
этого барьера. Во сколько раз следует сузить барьер, чтобы вероятность |
||||||||||||||
|
|
|
Рис.5.5 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
прохождения его протоном была такой же, как для электрона в этих же |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
условиях. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
18. Прямоугольный потенциальный барьер имеет ширину L = 0,1 нм. |
Для электрона разность |
|||||||||||||||||||||
U0 – E = 5 эВ. |
Определите, |
во сколько раз изменится коэффициент прозрачности D потенциального |
|||||||||||||||||||||||
|
|
|
|
U |
|
|
|
|
|
|
|
U |
|
|
|
|
барьера, |
если |
разность |
U0 – E |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
возрастает в 4 раза. |
|
|
|
|||||||
|
|
|
|
|
U0 |
|
|
|
|
|
|
|
|
U0 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19. Частица |
с |
энергией |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E = 10 эВ |
движется |
вдоль |
оси х, |
||
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
E |
встречая |
на |
своем |
|
пути |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
бесконечно |
|
широкий |
|||
|
|
–L |
0 |
|
|
L |
x |
–L |
0 |
L x |
|
||||||||||||||
|
|
|
|
прямоугольный |
потенциальный |
||||||||||||||||||||
|
|
|
|
|
Рис.5.6 |
|
|
|
|
|
|
|
Рис.5.7 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
барьер |
высотой |
U0 = 5 эВ. |
|||
Определите коэффициент преломления n на границе потенциального барьера. |
|
|
|
|
|
||||||||||||||||||||
20.Электрон с длиной волны де Бройля λ1 = 100 пм, двигаясь вдоль оси х, встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U0 = 100 эВ. Определите
длину волны де Бройля после прохождения барьера.
21.Частица с энергией Е = 50 эВ, двигаясь в положительном направлении оси х, встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U0 = 20 эВ. Определите
вероятность отражения частицы от этого барьера.
22.Частица массой m = 10–19 кг, двигаясь вдоль оси х со скоростью V = 20 м/с, встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U0 = 100 эВ. Определите коэффициент отражения R на границе потенциального барьера.
23.Электрон с энергией Е движется в положительном направлении оси х, встречая на своем пути барьер, ширина которого L и высота U0., если барьер имеет форму, показанную на рис.5.5.
24.Найти вероятность прохождения протона с энергией Е сквозь потенциальный барьер на
рис.5.6.
25.Найти вероятность прохождения частицы с массой m и энергией Е сквозь потенциальный барьер (рис.5.7), где U(x) = U0(1 – x2/L2).
23

vk.com/club152685050 | vk.com/id446425943
6. СТРОЕНИЕ АТОМА
Решая уравнение Шредингера для электрона в кулоновской яме ядра, показывает, чтоэлектрон в атоме может иметь следующие энергии:
En |
m Z 2e4 |
1 |
|
|
||
e |
|
|
|
, |
(6.1) |
|
2 4 0 |
2 2 |
|
n2 |
|||
где me – масса электрона, Z – атомный номер, n = 1, 2, 3… – главное квантовое число. Наиболее вероятное расстояние электрона в состоянии n от ядра:
rn |
|
4 0 2 |
n2 . |
(6.2) |
|
||||
|
2 |
|
|
|
me Ze
При n = 1 и Z = 1 это расстояние совпадает с радиусом первой боровской орбиты.
Модуль момента импульса электрона в атоме может принимать значения
|
|
|
. |
|
L |
1 |
(6. 3) |
Число ℓ = 0, 1, 2,…n – 1.. называется орбитальным квантовым числом. Проекция момента импульса на любую ось (например, z) тоже может принимать лишь определенные значения
L z m , |
(6.4) |
где mℓ = 0, ±1, ±2, …, ±ℓ и называется магнитным квантовым числом. Магнитное квантовое число
определяет также проекцию магнитного момента, создаваемого движением электрона вокруг ядра:
|
z B m . |
(6.5) |
||||
Модуль магнитного момента электрона |
|
|
|
|
|
|
|
|
|
B |
|
, |
|
|
|
1 |
(6.6) |
|||
где B e  2me = 0,927∙10–23 Дж/Тл – магнетон Бора. Отношение модулей орбитальных магнитного и
2me = 0,927∙10–23 Дж/Тл – магнетон Бора. Отношение модулей орбитальных магнитного и
механического моментов называется гиромагнитным отношенеим
|
|
|
L |
|
z |
L z B |
e 2me . |
(6.7) |
|
|
|
Электрон обладает также собственным механическим моментом импульса, равным
|
|
|
, |
|
Ls |
s s 1 |
(6.8) |
где s = 1/2–спиновое квантовое число. Соответствующий ему магнитный момент также квантован
|
s |
|
2 B |
|
. |
|
|
|
s s 1 |
(6.9) |
24

vk.com/club152685050 | vk.com/id446425943
|
|
|
|
|
|
|
|
|
j |
Проекции спинового момента импульса и магнитного момента на |
|||||||||||||
|
|
|
|
|
|
|
Ls |
направление z внешнего магнитного поля равны |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
Lℓ |
Lsz |
|
ms |
и sz 2 Bms , |
(6.10) |
|||||||||
|
μℓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
где ms – спиновое квантовое число, может принимать значения ±1/2. |
|||||||||||||
μj |
|
|
|
|
μs |
Гиромагнитное отношение для спиновых магнитного и |
|||||||||||||||||
|
|
|
|
механического моментов оказывается в два раза больше, чем для |
|||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
μΣ |
||||||||||||||||||||||
|
орбитальных моментов |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
Рис.6.1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
Ls |
|
sz Lsz 2 B e me . |
(6.11) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Орбитальный Lℓ и спиновый Ls моменты импульса электрона складываются и дают полный момент |
||||||||||||||||||||||
импульса электрона J (рис.6.1). Он квантуется так же |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
j j 1 |
(6.12) |
||||
где j |
|
s |
|
|
|
1 2 |
|
– внутреннее квантовое число. Проекция |
полного момента на направление |
||||||||||||||
|
|
|
|
||||||||||||||||||||
внешнего магнитного поля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jz |
m j , |
(6.13) |
||
где mj может принимать 2j + 1 значение от –j до j. Для описания состояния электрона в атоме используют четыре квантовых числа: n, ℓ, mℓ и ms. или n, ℓ, j, mj. Обычно для орбитального квантового
числа используют буквенные обозначения:
ℓ |
0 |
1 |
2 |
3 |
4 |
Обозначение |
s |
p |
d |
f |
g |
При втором способе описания термов используют следующие обозначения: состояния с ℓ = 0, 1, 2, 3,… обозначаются соответственно s, p, d, f, … Справа внизу указывается значение квантового числа j, а слева наверху величина 2s + 1 – мультиплетность терма. Например, 3p0 означает, что ℓ = 1, s = 1, j = 0.
Из-за разных гиромагнитных отношений для спинового и орбитального моментов суммарный
магнитный момент оказывается непараллельным суммарному механическому моменту. Поэтому вводится специальный коэффициент gЛ – фактор Ланде, который есть не что иное, как коэффициент пропорциональности между j и μj:
|
j |
gЛ B j, |
(6.14) |
|
gЛ 1 |
j j 1 s s 1 1 |
. |
(6.15) |
|
|
||||
|
|
2 j j 1 |
|
|
25
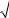
vk.com/club152685050 | vk.com/id446425943
Чтобы описать структуру сложного атома, надо знать состояния всех его электронов. В легких и средних атомах орбитальные моменты отдельных электронов складываются в суммарный орбитальный момент
L L 1 L 2 L 3 L i , |
(6.16) |
|||||
|
|
|
|
|
i |
|
а спиновые – в суммарный спиновый: |
|
|
|
|
|
|
|
|
|
S Lsi |
(6.17) |
||
|
|
|
|
i |
|
|
и полный момент |
|
|
|
|
|
|
|
|
|
J L S. |
(6.18) |
||
В тяжелых атомах полный момент равен сумме полных моментов отдельных электронов |
|
|||||
|
|
|
J ji , |
(6.19) |
||
|
|
|
|
i |
|
|
где ji L i Lsi . |
|
|
|
|
|
|
Магнитный момент атома |
|
|
|
|
|
|
|
J |
|
gЛ |
|
B . |
|
|
|
J J 1 |
(6.20) |
|||
Состояния атомов обозначаются так же, как это делается для отдельных электронов, но большими буквами. Например, 3P0 означает, что L = 1, S = 1, J = 0.
Порядок заполнения энергетических уровней в атоме определяется эмпирическими правилами Клечковского. Первое правило Клечковского: сначала будут заполняться уровни с наименьшей суммой квантовых чисел n + ℓ. Второе правило Клечковского: если два уровня имеют одинаковую сумму квантовых чисел n + ℓ, то первым будет заполняться уровень с меньшим n.
Электроны подчиняются принципу Паули: каждый энергетический уровень может быть заселен не более чем двумя электронами с противоположными спинами. Энергии некоторых состояний могут совпадать, т.е. может иметь место вырождение. В этом случае электроны заселяют состояния таким образом, чтобы спин S атома был максимален и, при этом по возможности максимальным было значение
L – правило Гунда.
При попадании атома во внешнее магнитное поле В с полем взаимодействуют как орбитальный, так и спиновый магнитные моменты электронов. Кроме того, эти моменты взаимодействуют между собой (спин-орбитальное взаимодействие). В случае слабого поля взаимодействие магнитных моментов с внешним полем меньше, чем спин-орбитальное взаимодействие, и атом приобретает дополнительную
энергию |
|
E B gЛ B mJ B , |
(6.21) |
которая зависит от квантового числа mJ, т.е. снимается вырождение по mJ. |
|
26

vk.com/club152685050 | vk.com/id446425943
В сильном магнитном поле спин-орбитальным взаимодействием можно пренебречь, связь между L и
S разрывается, и они проецируются на направление поля независимо друг от друга. В этом случае
E B B mL 2mS . |
(6.22) |
Примеры решения задач
1. Определите максимальное число электронов, находящихся в состояниях, описываемых данным главным квантовым числом n.
Решение. Каждому квантовому числу n соответствует n различных значений орбитального квантового числа ℓ: ℓ = 0, 1, 2,…, (n – 1). В свою очередь каждому значению ℓ соответствуют 2ℓ + 1 значения магнитного квантового числа: mℓ = 0, ±1, ±2,…, ±ℓ. На каждом уровне mℓ могут быть 2 электрона со спиновыми квантовыми числами ms = ±1/2. Полное количество электронов на оболочке n
n 1
равно N 2 2 1 2n2 .
0
2.Электрон в атоме находится в d-состоянии. Определите: а) орбитальный момент импульса
электрона; б) максимальное значение проекции момента импульса на направление внешнего магнитного поля.
Решение. Электрон в d-состоянии описывается орбитальным квантовым числом ℓ = 2. Модуль
орбитального момента при этом равен |
|
|
|
|
|
. |
Проекция |
момента импульса на |
|||
L |
1 |
6 |
|||||||||
направление внешнего магнитного поля может принимать значения |
L z |
m , |
соответствующие |
||||||||
различным величинам магнитного квантового числа |
mℓ: mℓ = 0, |
±1, |
±2. |
Максимальная проекция |
|||||||
орбитального момента соответствует максимальному значению mℓ = 2: L z |
2 . |
|
|
||||||||
3. Найти максимально возможный |
полный |
механический |
момент и |
соответствующее |
|||||||
спектральное обозначение терма атома натрия, валентный электрон которого имеет главное квантовое число n = 4.
Решение. Атом натрия имеет один электрон на внешней оболочке и спин этого электрона равен 1/2. Поэтому мультиплетность равна 2S + 1 = 2. Механический момент будет максимальным, если максимальным будет и орбитальное квантовое число. Данному n = 4 соответствует максимальное
значение L = 3. |
Внутреннее квантовое |
число |
J = L + S = 3 + 1/2 = 7/2. |
Максимально |
возможный |
|||||||||
механический |
момент |
будет |
равен |
|
|
|
|
|
|
|
|
2 . |
Обозначение |
|
|
J |
J J 1 |
7 9 2 2 |
63 |
||||||||||
соответствующего терма 2F7/2. |
|
|
|
|
|
|
|
|
|
|
|
|
||
4. Найти полное расщепление терма 2D3/2 |
в магнитном поле В = 2 |
Тл, |
считая его а) слабым, |
|||||||||||
б) сильным полем. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Состояние 2D3/2 означает, что J = 3/2, L = 2, S = 1/2. Фактор Ланде
27

vk.com/club152685050 | vk.com/id446425943
gЛ 1 |
3 2 5 2 1 2 3 2 2 3 |
|
4 |
. |
|
|
|
|
|
|
2 3 2 5 2 |
|
|
|
|||||||
|
5 |
|
|
|
|
|
|
|
||
а) Дополнительная энергия этого состояния в слабом магнитном поле E |
4 |
|
e B |
m |
|
. Квантовое |
||||
|
|
J |
||||||||
|
|
|
|
|
5 2me |
|
||||
|
|
|
|
|
|
|
||||
число mJ может принимать 2J + 1 значений от –J до J. Полное расщепление соответствует разности
энергий уровней с mJ = –3/2 и mJ = 3/2 2 E 2 |
4 |
|
e B |
|
3 |
. Подставляя численные данные, получим |
|
5 2me 2 |
|||||||
|
|
||||||
Δε = 276,9 10–6 эВ.
б) Энергетический сдвиг в сильном магнитном поле E = μBB(mL + 2mS). Квантовые числа mL и mS могут иметь значения от –2 до 2 и от –1/2 до 1/2 соответственно. Величина (mL + 2mS) будет иметь
максимальное значение 3 и минимальное значение –3. Максимальное расщепление будет равно
2 E 2 e B 3 . Подставляя численные значения, получим Δε = 692,3 10–6 эВ.
2me
Задачи для самостоятельного решения
1. Заполненной электронной оболочке соответствует главное квантовое число n = 3. Определите число электронов на этой оболочке, которые имеют одинаковые квантовые числа: а) ms = –1/2; б) mℓ = 0;
в) mℓ = –1, ms = 1/2.
2. Заполненной электронной оболочке соответствует главное квантовое число n = 4. Определите число электронов на этой оболочке, которые имеют одинаковые квантовые числа: а) mℓ = –3; б) ms = 1/2, mℓ = 2; в) ms = –1/2, mℓ = 1.
3. Сколько электронов в атоме могут иметь одинаковые квантовые числа: а) n, ℓ, mℓ, ms; б) n, ℓ,
mℓ.
4.Валентный электрон атома Na находится в состоянии с n = 3, имея при этом максимально
возможный полный механический момент. Каков его магнитный момент в этом состоянии?
5.Определите во сколько раз орбитальный момент импульса Lℓ электрона, находящегося в f- состоянии, больше, чем для электрона в р-состоянии.
6.1s электрон атома водорода, поглотив фотон с энергией Е = 12,1 эВ, перешел в возбужденное
состояние с максимально возможным орбитальным квантовым числом. Определите изменение момента импульса Lℓ орбитального движения электрона.
7. Определите суммарное максимальное число s-, p-, d-, f- и g-электронов, которые могут находиться на N- и O-оболочках атома.
8. Найти кратность вырождения 2p, 3d и 4f состояний с максимально возможными полными
механическими моментами.
28
vk.com/club152685050 | vk.com/id446425943
9.Написать электронную формулу элемента №79 и объяснить порядок заполнения уровней.
10.Написать электронную формулу элемента № 47 и объяснить порядок заполнения уровней.
11.У какого элемента заполнены K-, L- и M-оболочки и 4s-подоболочка, а также наполовину заполнена 4p-подоболочка?
12.Найти с помощью правила Гунда полный механический момент атома в основном состоянии, если его незаполненная подоболочка содержит: а) три d-электронов, б) семь d-электронов.
13.Найти с помощью правила Гунда полный механический момент атома в основном состоянии, если его незаполненная подоболочка содержит: а) три p-электронов, б) четыре p-электронов.
14.Определить спиновый механический момент атома в состоянии D2, если максимальное значение проекции магнитного момента в этом состоянии равно 4μВ.
15.Найти с помощью правила Гунда магнитный момент основного состояния атома, незамкнутая подоболочка которого заполнена ровно наполовину пятью электронами.
16.Возбужденный атом имеет электронную конфигурацию 1s22s22p3d и находится при этом в
состоянии с максимально возможным полным механическим моментом. Найти магнитный момент атома в этом состоянии.
17. Найти полный механический момент атома в состоянии с S = 3/2 и L = 2, если
известно, что магнитный момент его равен 0.
18.Найти возможные значения полных механических моментов атомов, находящихся в состояниях 4P и 5D.
19.Сколько и какие значения квантового числа J может иметь атом в состоянии с квантовыми числами S и L, равными соответственно а) 2 и 3; б) 3 и 3; в) 5/2 и 2
20.На сколько подуровней расщепится в слабом магнитном поле терм: а) 3P0; б) 2F5/2; в) 4D1/2?
Привести схему уровней.
21.Атом находится в слабом магнитном поле с индукцией В = 0,25 Тл. Найти полную величину расщепления в электрон-вольтах следующих термов: а) 1P; б) 3F4. Привести схему уровней.
22.Атом находится в слабом магнитном поле с индукцией В = 1,0 Тл. Найти полную величину расщепления в электрон-вольтах следующих термов: а) 1S; б) 2D5/2. Привести схему уровней.
23.Определить максимальную энергию Е магнитного взаимодействия атома, находящегося в состоянии 1D с магнитным полем, индукция которого а) B = 1 Тл (слабое поле), б) В = 50 Тл (сильное
поле). Привести схемы уровней.
24.Атом находится в сильном магнитном поле с индукцией В = 5 Тл. Найти полную величину расщепления в электрон-вольтах следующих термов: а) 1P; б) 3F4. Привести схему уровней.
25.Написать спектральное обозначение терма, кратность вырождения которого равна 7, а квантовые числа L и S связаны соотношением L = 3S.
7.РЕНТГЕНОВСКИЕ СПЕКТРЫ АТОМОВ
29
