1.Рівномірний розподіл:

Рівномірний розподіл (неперервний) — в теорії імовірностей розподіл, який характеризується тим, що ймовірність будь-якого інтервала залежить тільки від його довжини.

Кажуть, що випадкова величина має неперервний рівномірний розподіл на відрізку ,де , якщо щільність має вигляд:

Пишуть: . Деколи значення щільності в граничних точках і міняють на інші, наприклад .Так як інтеграл Лебега від щільності не залежить від поведінки останньої на множинах міри нуль, ці варіації не впливають на знаходження зв'язаних з цим розподілом імовірностей.

Інтегруючи визначену вище щільність отримуємо:

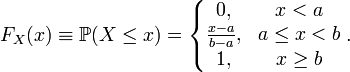
Оскільки щільність рівномірного розподілу розривна в граничних точках відрізка , то функція розподілу в цих точках не є диференційовною. В інших точках справедлива рівність:

.

2.Знаходження параметрів прямої регресії:

???????????????

№ 6:

1.Локальна теорема Лапласа:

Локальна теорема Муавра — Лапласа описує наближення нормального розподілу до біноміального розподілу. Є окремим випадком центральної граничної теореми.

Теорема

Якщо , тоді для k в -околі точки np, існує наближення

Гранична форма теореми стверджує, що

для

Додаток

Можливо, формулювання стає ясним не відразу, проте практичний зміст теореми простий: при великих значеннях n імовірність спостерігаючи рівно m успіхів можна приблизно розраховувати за формулою:

Якщо вас цікавить імовірність того, що число успіхів буде лежати в деяких межах - - у розрахунках допомагає інтегральна теорема Муавра-Лапласа.

2.Числові характеристики розсіяння:

Для характеристики розсіювання значень випадкової величини відносно її центра розподілу

(математичного сподівання) вводять числову характеристику – дисперсію випадкової величини.

Позначається D[ X ] . За означенням, дисперсією випадкової величини X називається математичне

сподівання квадрату відхилення випадкової величини від її математичного сподівання

D[ X ]= M [X − M [X ] ]².

Дисперсія обчислюється за формулами

D[X ] =∑ (xi − mx )² pi

i =1 для дискретних випадкових величин, і

+∞

D[X ]= ∫ (x − mx )² f ( x)d x

−∞ для неперервних випадкових величин..

Дисперсія є кількісною оцінкою відхилення випадкової величини від її математичного

сподівання. Проте, оскільки дисперсія має розмірність квадрата випадкової величини, то для

x =/ D[ X ] , яка називається середнім

оцінки міри розсіювання використовують характеристику

квадратичним або стандартним відхиленням випадкової величини. Оскільки D[ X ] ≥ 0 , то і

x = /D[ X ] ≥0. Розмірність середнього квадратичного відхилення співпадає з розмірністю

випадкової величини.

№ 2:

1.Теорема множення ймовірностей:

Добутком двох подій А і В називається подія С, що полягає у здійсненні під час одиничного випробовування й події А, і події В.

Подія А називається від події В, якщо ймовірність події А не залежить від того, відбулась чи ні подія В.

Дві події А та В називають залежними, якщо ймовірність настання однієї з них залежить від того, настала друга подія чи ні.

Умовною ймовірністю РА(В) події В називається ймовірність події В, знайдена в припущенні, що подія А вже настала.

З означення назалежних подій випливає, що настання однієї з них не змінює ймовірності настання другої. Тому для незалежних подій справджуються рівності:

Отже, умовні ймовірності незалежних подій дорівнюють їх безумовним імовірностям.

Теорема 1. Імовірність добутку двох залежних подій А і В дорівнює добутку ймовірності однієї з них на умовну ймовірність другої, яка знайдена з припущенням того, що перша подія настала, тобто

Доведення. Нехай з усієї кількості n елементарних подій k сприяють події А і нехай з цих подій l сприяють події В, а, отже і події АВ. Тоді:

що й треба було довести.

Теорема 2. Імовірність добутку двох незалежних подій А і В дорівнює добутку імовірностей цих подій, тобто

Доведення. Якщо А і В - незалежні події, то

і формула

перетворюється в формулу .